Что такое директриса в математике

Директриса в математике — это кривая, которая задает местоположение всех директрисальных точек исходной кривой. Она играет важную роль при решении геометрических задач и изучении свойств кривых. Узнайте, как понять и использовать директрису в математике.

Директриса – это одно из важнейших понятий в области математики, которое нашло свое применение в различных научных и инженерных областях. Это понятие возникло в первой половине XIX века и было впервые введено французским математиком Шарлем Жюлем Мари Луи Ларрейем Дирихле.

Определение директрисы связано с геометрией и алгеброй. В геометрии директриса – это прямая, которая определяется как множество точек, равноудаленных от точки и от данной прямой, называемой директрисой. В алгебре директриса – это график кривой, который может быть получен с помощью алгебраического уравнения.

Применение директрисы в математике

Директриса имеет широкое применение в различных областях математики, физики и инженерии. Например, она может быть использована для определения фокусных свойств эллипса или параболы. Также директриса используется при решении задач оптимизации, в теории вероятностей, в теории управления и в других областях.

Директриса играет важную роль в решении различных задач, таких как определение траектории движения тела под действием силы тяжести, оптимальное размещение объектов, анализ многомерных данных и другие. Изучение директрисы позволяет более глубоко понять и описать различные явления и процессы в математике и ее приложениях.

Что такое директриса в математике?

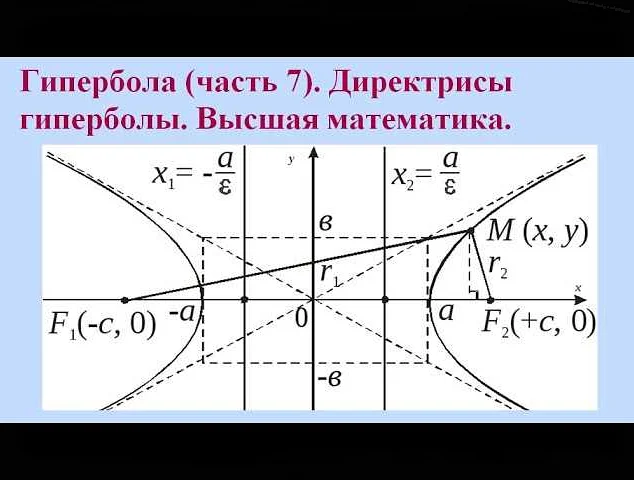
Директриса широко используется в геометрии и физике. Например, в геометрии директриса применяется для определения параболы и гиперболы. В случае параболы директрисой является прямая, находящаяся на одинаковом расстоянии от фокуса и от оси симметрии параболы. В случае гиперболы директрисами являются две прямые, расположенные симметрично относительно оси симметрии и также находящиеся на одинаковом расстоянии от фокуса.

В физике директриса используется, например, при описании движения небесных тел. Орбиты планет и комет могут быть описаны с помощью конических сечений, и в этом контексте директриса играет важную роль.

Таким образом, директриса является важным понятием в математике и имеет широкое применение в различных областях науки и техники.

Определение и применение

Директриса имеет широкое применение в математике и физике. Она используется, например, при описании конических сечений, таких как эллипсы, параболы и гиперболы. Директриса позволяет определить форму конического сечения и свойства, связанные с его геометрией.

Директриса также играет важную роль в фокусно-директрисной форме уравнения параболы. Это уравнение позволяет определить положение фокуса и директрисы параболы и использовать их для графического представления параболической кривой.

Помимо геометрических приложений, директриса также используется в оптике и механике. Например, она помогает описывать лучи света, отражающиеся или преломляющиеся на поверхности конического отражателя или линзы.

В целом, понимание директрисы и ее применение позволяют решать широкий спектр задач, связанных с геометрией, оптикой, механикой и другими областями науки и техники.

Роль директрисы в геометрии

Одним из основных применений директрисы является определение кривых второго порядка, таких как эллипсы, параболы и гиперболы. Для каждой из этих кривых существует соответствующая директриса, которая помогает определить форму и расположение кривой.

Например, для параболы директриса — это прямая, которая находится на равном удалении от фокуса и директрисы. Это свойство позволяет определить точки на параболе путем отражения лучей, падающих перпендикулярно директрисе.

Кроме того, директриса используется для определения касательных и нормалей к кривым. Например, касательная к гиперболе в точке пересечения с директрисой будет параллельна самой директрисе.

Директриса также играет роль в определении фокусных свойств кривых. Например, эллипс характеризуется тем, что сумма расстояний от любой точки на нем до двух фокусов равна постоянной величине, которая является длиной большой оси. Директриса эллипса определяет это расстояние и позволяет определить фокусные свойства кривой.

Таким образом, директриса играет важную роль в геометрии, предоставляя информацию о форме, положении и свойствах различных кривых. Ее применение распространяется на множество геометрических конструкций и находит применение в различных областях науки и техники.

Как найти директрису?

Шаг 1: Задайте уравнение гиперболы или эллипса. Уравнение должно быть в стандартной форме и содержать параметр a, который определяет полуоси гиперболы или эллипса.

Шаг 2: Найдите фокусное расстояние c с использованием формулы c = √(a^2 + b^2), где b — длина короткой полуоси.

Шаг 3: Рассчитайте координаты фокусов (c, 0) и (-c, 0).

Шаг 4: Найдите уравнение директрисы в зависимости от типа кривой:

• Для гиперболы уравнение директрисы имеет вид x = ±(a^2/c), где a^2/c — расстояние от центра гиперболы до директрисы.
• Для эллипса уравнение директрисы имеет вид x = ±(a^2/c), где a^2/c — расстояние от центра эллипса до директрисы.

Шаг 5: Постройте директрису на координатной плоскости, используя найденное уравнение. Директриса будет представлять собой вертикальные прямые, проходящие через координаты фокусов.

Поиск директрисы позволяет лучше понять геометрические свойства гиперболы и эллипса, а также применять их в различных областях, таких как физика, инженерия и экономика.

Примеры из реальной жизни

1. Планирование бюджета

Директриса в математике может использоваться для оптимизации планирования бюджета. Например, она может помочь определить, сколько средств необходимо выделить на определенные категории расходов, основываясь на доступных ресурсах и приоритетах.

2. Управление временем

В работе, директриса в математике может помочь в управлении временем. Она может помочь определить, сколько времени занимает выполнение конкретной задачи или процесса, и оптимизировать распределение времени для достижения максимальной эффективности.

3. Прогнозирование и анализ данных

Директриса в математике также может использоваться для прогнозирования и анализа данных. Например, она может помочь в предсказании будущих трендов или поведения рынка на основе имеющихся данных, что может быть полезно в бизнесе или научных исследованиях.

4. Решение сложных проблем

Директриса в математике может быть полезной при решении сложных проблем. Она может помочь структурировать проблему, разбить ее на более простые части и определить наиболее эффективные стратегии для ее решения.

5. Оптимизация процессов

В различных областях, директриса в математике может быть использована для оптимизации процессов. Например, она может помочь определить оптимальный маршрут доставки или распределение ресурсов для повышения эффективности и снижения затрат.

Видео по теме:

Вопрос-ответ:

Что такое директриса в математике?

Директриса — это геометрическое место точек, которые находятся на одинаковом расстоянии от прямой и отражающей прямой. Она представляет собой кривую, которая параллельна отражающей прямой и находится на одинаковом расстоянии от неё.

Как определить директрису?

Чтобы определить директрису, необходимо знать уравнение прямой и уравнение отражающей прямой. Далее, используя геометрические свойства, можно найти уравнение директрисы, которая будет параллельна отражающей прямой и находиться на одинаковом расстоянии от неё.

Какие применения имеет директриса в математике?

Директриса имеет широкое применение в математике и геометрии. Она используется при изучении кривых, таких как парабола, эллипс и гипербола. Директриса помогает определить геометрические свойства этих кривых, а также решать различные задачи, связанные с ними.

Какую роль играет директриса в фокусно-директрисном определении параболы?

В фокусно-директрисном определении параболы директриса играет роль геометрического места точек, которые находятся на одинаковом расстоянии от фокуса и отражающей прямой. Она помогает определить форму параболы и установить связь между геометрическими свойствами параболы и её уравнением.

В каких областях науки применяется понятие директрисы?

Понятие директрисы применяется в различных областях науки, включая математику, физику, астрономию и технику. Например, в физике директриса может использоваться для описания траекторий движения тел, а в астрономии — для анализа орбит планет и комет. Также директриса находит применение в технических расчётах, связанных с оптикой и зеркалами.

Что такое директриса в математике?

Директриса — это линия, которая описывает множество точек, равноудаленных от фиксированной прямой и движущейся точки. В математике директриса играет важную роль в изучении кривых.

Как можно определить директрису кривой?

Для определения директрисы кривой необходимо найти точки, которые равноудалены от фиксированной прямой и движущейся точки. Это можно сделать с помощью геометрической конструкции или аналитически, используя уравнения кривой.

Директриса в фокусе

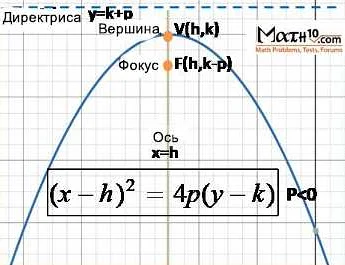
Директриса определяется как множество точек, для которых расстояние до фокуса кривой равно расстоянию до прямой, называемой директрисой. Точка фокуса и директриса являются важными характеристиками директрисы кривой и определяют ее форму и свойства.

Интересно, что директриса находится всегда вне кривой и имеет особую геометрическую связь с ней. Например, для параболы директриса — вертикальная прямая, проходящая через фокус параболы. Директриса параболы играет важную роль в определении ее формы и особых свойств, таких как фокусное свойство и отражательное свойство.

Директриса также активно применяется в других областях математики и физики. Например, в оптике директриса используется для описания формы и расположения зеркал. В эллиптических координатах директриса играет важную роль в описании эллипсов и гипербол, а также в решении уравнений в этих координатах.

Таким образом, директриса является важным геометрическим понятием, которое имеет широкое применение в различных областях математики и физики. Понимание директрисы и ее свойств позволяет лучше понять и анализировать форму кривой и решать разнообразные задачи, связанные с ее геометрическими характеристиками.

Значение директрисы в кривых второго порядка

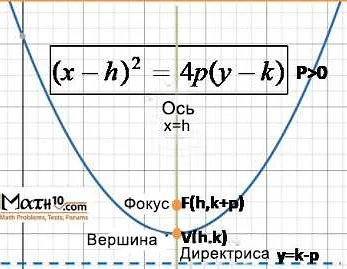
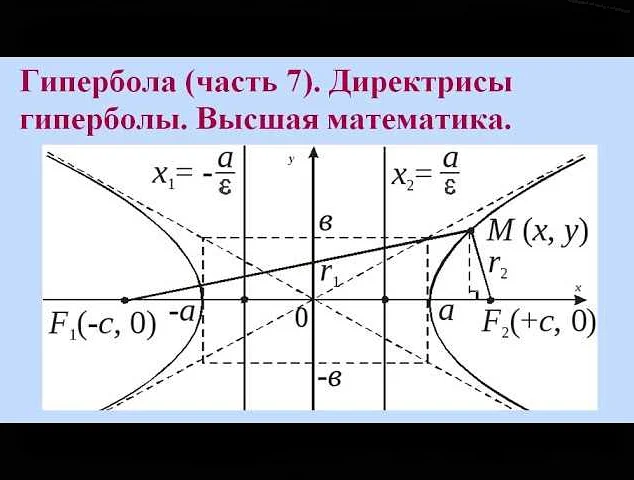
В кривых второго порядка директриса определяется следующим образом: для каждой точки кривой существует такая прямая, называемая директрисой, что расстояние от этой точки до директрисы равно расстоянию от этой точки до фокуса кривой.

Значение директрисы в кривых второго порядка заключается в том, что она позволяет определить форму и свойства кривой. Директриса является важным элементом в геометрическом описании кривых и позволяет анализировать их свойства и использовать их в различных задачах.

Примеры кривых второго порядка, где директриса играет важную роль, включают параболу и эллипс. В параболе директриса – это прямая, расположенная на равном расстоянии от фокуса до оси симметрии параболы. В эллипсе директрисы – это две прямые, проходящие через фокусы и перпендикулярные оси симметрии эллипса.

Использование директрисы в кривых второго порядка позволяет более точно определить и анализировать их форму, свойства и особенности. Это важный инструмент в математике, который находит применение в различных областях, включая физику, инженерию и компьютерную графику.