Какую длину имеет математический маятник с периодом колебания 2 с

Математический маятник с периодом колебания равным 2 с имеет определенную длину, которую можно вычислить с использованием формулы. Узнайте, как определить длину такого маятника и как она связана с его периодом колебания.

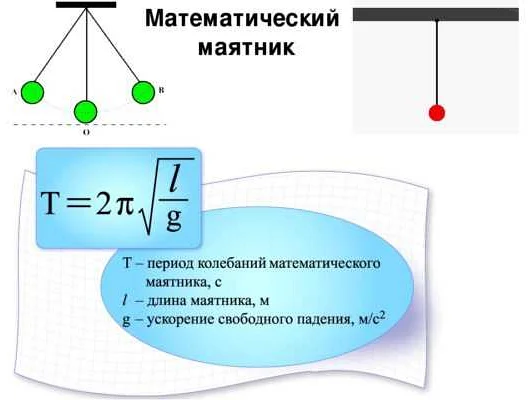
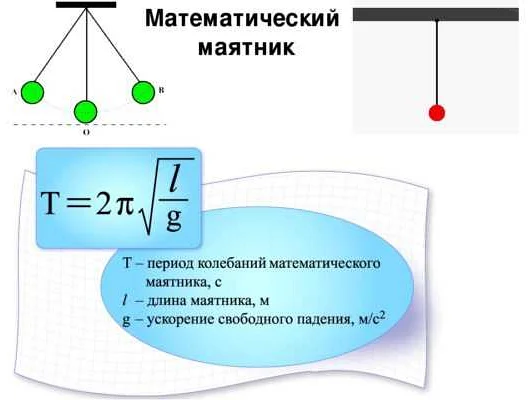
Математический маятник — это простейшая модель колебаний, которая состоит из невесомой нити и точечной массы, подвешенной на конце этой нити. Он является одним из основных объектов изучения в классической механике, так как полностью аналитически решается уравнением гармонического осциллятора.

Период колебаний математического маятника зависит от его длины. Формула для расчета периода колебаний выглядит следующим образом:

T = 2π√(l/g)

Здесь T — период колебаний, l — длина маятника, g — ускорение свободного падения.

Если у нас есть заданный период колебаний, например 2 секунды, мы можем использовать эту формулу, чтобы найти необходимую длину математического маятника.

Что такое математический маятник?

Основные характеристики математического маятника:

Длина нити: это расстояние от точки подвеса до центра масс маятника. Длина нити влияет на период колебаний — время, за которое маятник проходит полный цикл колебаний. Чем длиннее нить, тем больше период колебаний.

Масса маятника: масса тела, которое закреплено на нити. Масса также влияет на период колебаний — чем больше масса, тем больше период колебаний.

Математический маятник является простым идеализированным объектом, который позволяет упростить изучение колебаний и применить математические методы для их анализа. Он используется не только в физике и математике, но и в других науках, таких как инженерия, астрономия и биология, для моделирования и анализа колебательных процессов.

Механическое устройство для изучения колебаний

Одним из примеров такого устройства является математический маятник. Он представляет собой маятник, в котором время одного полного колебания, также называемое периодом, составляет 2 секунды.

Математический маятник обладает определенной длиной, которая влияет на его период колебаний. Длина математического маятника определяется геометрическими параметрами, такими как длина подвеса и масса груза, и может быть регулируемой.

Изучение колебаний с помощью механических устройств позволяет ученым и студентам более глубоко понять законы и принципы колебательных процессов. Эти устройства позволяют проводить эксперименты с различными параметрами и наблюдать их влияние на колебания.

Математический маятник с периодом колебания 2 секунды является одним из наиболее простых и понятных примеров механических устройств для изучения колебаний. Он позволяет учащимся и исследователям легко проводить эксперименты и измерять период колебаний с высокой точностью.

Таким образом, механические устройства для изучения колебаний играют важную роль в обучении и исследовании физики и механики. Они позволяют наглядно продемонстрировать различные типы колебательных процессов и помогают учащимся лучше понять их основные законы и свойства.

Что влияет на период колебания маятника?

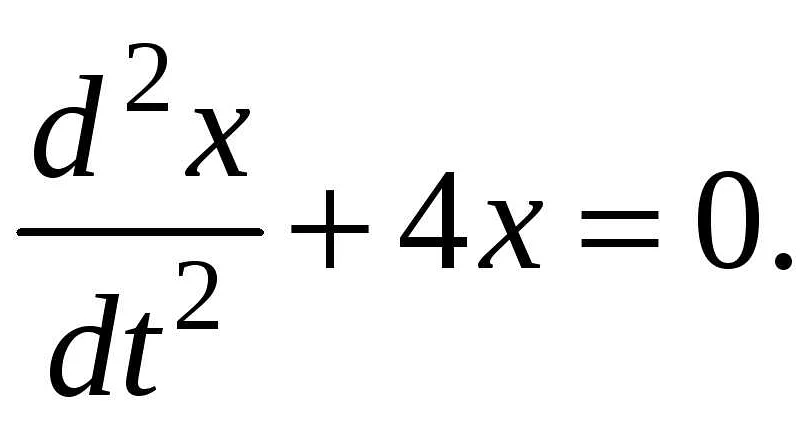
Период колебания математического маятника зависит от нескольких факторов:

1. Длины маятника: период колебаний прямо пропорционален квадратному корню из длины маятника. Чем длиннее маятник, тем медленнее будет его колебание.
2. Силы тяжести: период колебания также зависит от силы тяжести. Чем больше сила тяжести, тем быстрее будет колебаться маятник.
3. Массы маятника: период колебания не зависит от массы маятника. Это означает, что маятники разной массы будут колебаться с одинаковым периодом при одинаковых условиях.
4. Угла отклонения: период колебания может зависеть от угла отклонения от положения равновесия. Обычно малые углы отклонения дают периоды, близкие к тем, что были бы при отсутствии диссипации энергии.
5. Среды, в которой осуществляется колебание: период колебания может быть влияние на среду, в которой маятник колеблется. Например, при наличии сопротивления воздуха маятник может колебаться медленнее.

Изучение этих факторов позволяет более глубоко понять и предсказывать поведение математического маятника и его период колебания.

Длина маятника и сила тяжести

Длина математического маятника оказывает влияние на его период колебания. Период колебания математического маятника определяется формулой:

T = 2π√(l/g)

где T — период колебания, l — длина маятника, g — ускорение свободного падения.

Ускорение свободного падения на Земле принимается равным примерно 9,8 м/с². Подставляя это значение в формулу, получаем:

T = 2π√(l/9.8)

Таким образом, длина маятника напрямую влияет на его период колебания. Чем длиннее маятник, тем больше времени ему требуется для совершения полного колебательного движения. И наоборот, чем короче маятник, тем быстрее он будет совершать колебания. Это связано с тем, что при большей длине маятника, сила тяжести будет действовать на него с меньшей интенсивностью, а при малой длине маятника сила тяжести будет действовать с большей силой.

Длина маятника также влияет на амплитуду колебаний. Амплитуда — это максимальное отклонение маятника от положения равновесия. Чем больше длина маятника, тем больше его амплитуда.

Длина маятника (l), мПериод колебания (T), с

0,5	1,00
1,0	1,41
1,5	1,73
2,0	2,00
2,5	2,24

В таблице представлены значения периода колебания для разных длин маятника, рассчитанные по указанной формуле. Из таблицы видно, что при увеличении длины маятника период колебания также увеличивается.

Каков период колебания математического маятника?

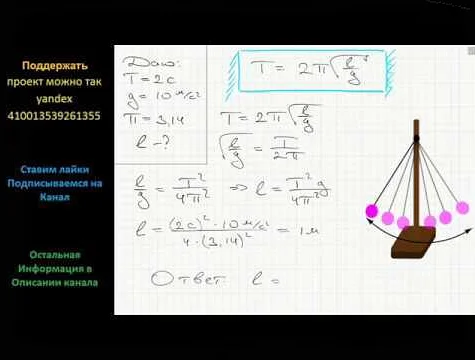
Период колебания математического маятника зависит от его длины. Для маятника с длиной равной линейной расстоянию от точки подвеса до центра масс, период колебания может быть рассчитан с использованием формулы:

T = 2π√(L/g)

где T — период колебания, L — длина маятника, g — ускорение свободного падения.

Для маятника с периодом колебания равным 2 секунды, мы можем использовать эту формулу для определения его длины. Подставляя известные значения в формулу, мы можем рассчитать длину маятника:

L = (T/2π)^2 * g

В данном случае, период колебания T равен 2 секунды и ускорение свободного падения g примерно равно 9.8 м/с^2. Подставляя эти значения в формулу, получаем:

L = (2/2π)^2 * 9.8 ≈ 0.994 метров

Таким образом, длина математического маятника с периодом колебания 2 секунды составляет примерно 0.994 метра.

Математическая формула для расчета периода колебания

Период колебания математического маятника можно вычислить с помощью следующей формулы:

T = 2π√(l/g)

где:

• T — период колебания математического маятника в секундах;
• π — математическая константа, приближенное значение которой равно 3.14159;
• l — длина математического маятника в метрах;
• g — ускорение свободного падения, приближенное значение которого на Земле равно около 9.8 м/с².

Используя данную формулу, можно рассчитать период колебания математического маятника с известной длиной.

Как изменить период колебания на 2 секунды?

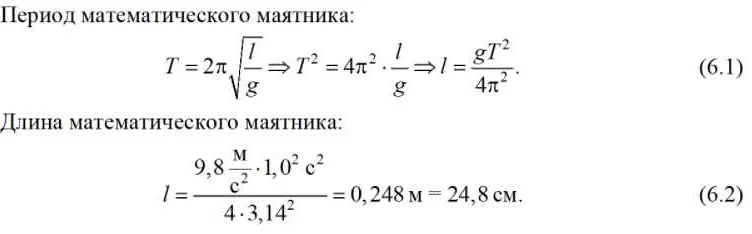
Длина математического маятника оказывает прямое влияние на его период колебания. Чтобы изменить период колебания на 2 секунды, необходимо изменить длину маятника. Период колебания определяется формулой:

Т = 2π√(L/g)

Где T — период колебания, L — длина маятника, g — ускорение свободного падения.

Для изменения периода колебания на 2 секунды, необходимо решить уравнение относительно L:

T = 2 = 2π√(L/g)

Для этого нужно выразить L:

L = (T/2π)^2 * g

Таким образом, чтобы получить период колебания равный 2 секундам, необходимо подставить значение ускорения свободного падения и решить уравнение для получения необходимой длины маятника.

Расчет длины математического маятника с нужным периодом

Формула для расчета периода колебания математического маятника имеет вид:

T = 2π√(l/g)

Где T — период колебания, l — длина маятника, g — ускорение свободного падения (приближенное значение 9.8 м/с² на Земле).

Из данной формулы можно выразить длину маятника:

l = (T²g)/(4π²)

Подставляя значение периода, равное 2 секунды, и ускорение свободного падения, получаем следующий результат:

l = (2² * 9.8) / (4 * 3.14²) ≈ 1.006 метра

Таким образом, длина математического маятника должна составлять примерно 1.006 метра, чтобы его период колебания был равен 2 секундам.

Какую роль играет сила тяжести в колебаниях маятника?

Сила тяжести играет основную роль в колебаниях математического маятника. Математический маятник представляет собой механическую систему, состоящую из невесомого стержня или нити, на одном конце которого закреплена точечная масса.

Когда маятник отклоняется от равновесного положения и отпускается, сила тяжести начинает действовать на точечную массу, стремясь вернуть ее в положение равновесия. Это приводит к возникновению колебательного движения маятника.

Сила тяжести создает возвращающую силу, которая направлена в сторону равновесия и пропорциональна смещению массы от положения равновесия. Чем больше смещение, тем сильнее сила, и тем большую скорость приобретает маятник при движении в сторону равновесия. По мере приближения к равновесию, сила тяжести уменьшается, и маятник начинает замедляться.

Период колебаний математического маятника зависит от длины нити и силы тяжести, амплитуда колебаний — от начального отклонения. Сила тяжести определяет скорость и направление колебаний маятника, а также его энергию.

ПараметрРоль в колебаниях маятника

Длина нити	Определяет период колебаний маятника: чем длиннее нить, тем больше период
Сила тяжести	Создает возвращающую силу, определяет скорость и направление колебаний, а также энергию маятника
Начальное отклонение	Определяет амплитуду колебаний: чем больше отклонение, тем больше амплитуда

Вопрос-ответ:

Какая формула позволяет рассчитать длину математического маятника с периодом колебания 2 секунды?

Длина математического маятника с периодом колебания 2 секунды можно рассчитать по формуле T=2π√(L/g), где T — период колебания, L — длина маятника, g — ускорение свободного падения.

Какое значение ускорения свободного падения следует использовать при расчете длины математического маятника с периодом колебания 2 секунды?

При расчете длины математического маятника с периодом колебания 2 секунды следует использовать значение ускорения свободного падения g, которое обычно принимается равным 9,8 м/с^2.

Как можно определить длину математического маятника с периодом колебания 2 секунды, если известно ускорение свободного падения?

Длину математического маятника с периодом колебания 2 секунды можно определить по формуле L = (T/2π)^2 * g, где L — длина маятника, T — период колебания, g — ускорение свободного падения.

Как зависит длина математического маятника с периодом колебания 2 секунды от ускорения свободного падения?

Длина математического маятника с периодом колебания 2 секунды зависит от ускорения свободного падения по формуле L = (T/2π)^2 * g, то есть пропорционально квадрату ускорения свободного падения.

Как изменится длина математического маятника с периодом колебания 2 секунды, если ускорение свободного падения увеличится на 10%?

Если ускорение свободного падения увеличится на 10%, то длина математического маятника с периодом колебания 2 секунды изменится пропорционально квадрату ускорения свободного падения. То есть, L1 = (T/2π)^2 * g1, а L2 = (T/2π)^2 * g2, где L1 и L2 — длины маятника при разных ускорениях, g1 и g2 — ускорения при разных значениях. Подставляя значения, можно рассчитать новую длину маятника.

Связь между силой тяжести и периодом колебания

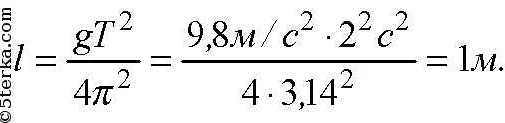
Период колебания математического маятника зависит от его длины и силы тяжести. В частности, уравнение периода колебания математического маятника можно записать следующим образом:

Т = 2π√(l/g),

где T — период колебания, l — длина маятника, g — ускорение свободного падения.

Из данного уравнения видно, что период колебания обратно пропорционален корню квадратному из силы тяжести. Это означает, что при увеличении силы тяжести период колебания будет уменьшаться, а при уменьшении силы тяжести период колебания будет увеличиваться.

Таким образом, изменение силы тяжести может оказывать значительное влияние на период колебания математического маятника. Это связано с тем, что сила тяжести является основной силой, определяющей движение маятника.

Видео по теме: