Что такое дополнение множеств в математике
Содержимое
- 1 Что такое дополнение множеств в математике
- 1.1 Дополнение множеств в математике
- 1.2 Определение дополнения множества
- 1.3 Свойства дополнения множества
- 1.4 Дополнение множества и операции над множествами
- 1.5 Примеры дополнения множества
- 1.6 Дополнение пустого множества
- 1.7 Отображение дополнения множества на диаграмме Эйлера–Венна
- 1.8 Дополнение множества и теория вероятностей
- 1.9 Видео по теме:
Дополнение множества в математике – это операция, которая позволяет вычислить элементы, которые присутствуют в одном множестве, но отсутствуют в другом. Узнайте, как выполнять операцию дополнения множества и применять ее в математических расчетах.
В математике дополнение множества – это операция, которая позволяет найти все элементы, не принадлежащие данному множеству. Оно обозначается символом ∁. Дополнение может быть выполнено для любого множества в другом множестве, которое называется универсальным множеством, и определяется относительно него.
Свойства дополнения множества позволяют рассматривать их в контексте других операций, таких как объединение, пересечение и разность множеств. Например, дополнение объединения двух множеств равно пересечению дополнений этих множеств.
Дополнение множества можно представить в виде Venn-диаграммы, где дополнение обозначается как область, не попадающая внутрь данного множества. Это наглядно показывает, что дополнение – это все элементы, которые не принадлежат данному множеству.
Примеры применения дополнения множества в математике могут быть разнообразными. Например, при решении задач на теорию множеств, оно может использоваться для нахождения отрицания утверждений, проверки эквивалентности множеств, а также для определения множества комплементарных элементов.
Дополнение множеств в математике
Формально, дополнение множества A определяется следующим образом:
Дополнение множества AAc
| Определение | {x ∈ U | x ∉ A} |
Где U — универсальное множество, содержащее все возможные элементы.
Свойства дополнения множеств:
- A ∩ Ac = ∅ (пустое множество)
- A ∪ Ac = U (универсальное множество)
- (Ac)c = A (двойное дополнение)
- A ∩ U = A (пересечение с универсальным множеством)
- A ∪ ∅ = A (объединение с пустым множеством)
Например, пусть U = {1, 2, 3, 4, 5} и A = {1, 2}. Тогда дополнение множества A будет равно Ac = {3, 4, 5}.
Дополнение множества играет важную роль в различных областях математики, таких как теория множеств, математическая логика, анализ и другие.
Определение дополнения множества
Дополнение множества A обозначается как \(A^c\) или \(\overline{A}\).
Множество, из которого берутся элементы для дополнения, называется универсальным множеством и обозначается как U.
Таким образом, дополнение множества A в универсальном множестве U можно определить как:
\(A^c = \{x \in U | x
ot\in A\}\)
Это означает, что дополнение множества A состоит из всех элементов универсального множества U, которые не принадлежат множеству A.
Дополнение множества можно представить графически с помощью диаграммы Эйлера-Венна. На диаграмме дополнение множества A обозначается областью, не пересекающейся с областью самого множества A.
Например, если универсальное множество U — это множество всех студентов в университете, а множество A — это множество студентов, которые изучают математику, то дополнение множества A будет состоять из всех студентов, которые не изучают математику.
Свойства дополнения множества
- Дополнение множества A обозначается как A’ или Ac.
- Дополнение множества A относительно универсального множества U представляет собой все элементы, которые не принадлежат множеству A и принадлежат множеству U.
- Если A и B — два множества, то дополнение их объединения равно пересечению дополнений: (A ∪ B)’ = A’ ∩ B’.
- Если A и B — два множества, то дополнение их пересечения равно объединению дополнений: (A ∩ B)’ = A’ ∪ B’.
- Дополнение дополнения множества A равно самому множеству A: (A’)’ = A.
- Дополнение пустого множества равно универсальному множеству: ∅’ = U.
- Дополнение универсального множества равно пустому множеству: U’ = ∅.
Свойства дополнения множества позволяют выполнять различные операции с множествами и устанавливать их взаимосвязи. Эти свойства являются основой для изучения множественной алгебры и других разделов математики.
Дополнение множества и операции над множествами
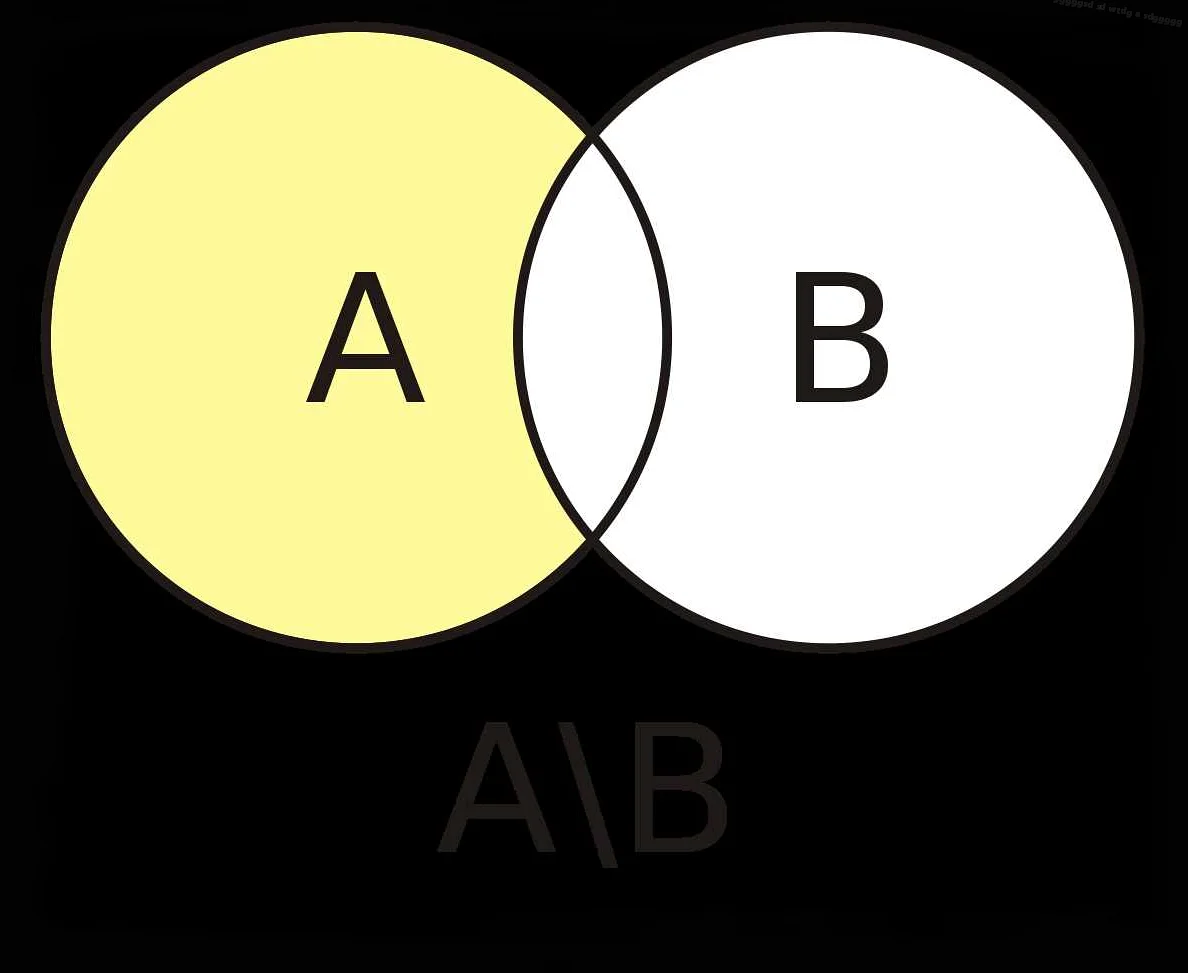
Операции над множествами позволяют комбинировать множества и выполнять различные действия с их элементами. Основными операциями над множествами являются объединение, пересечение, разность и симметрическая разность.
- Объединение множеств A и B (обозначается как A ∪ B) — результатом данной операции является множество, которое содержит все элементы, которые принадлежат хотя бы одному из множеств A и B. Например, если A = {1, 2, 3} и B = {3, 4, 5}, то A ∪ B = {1, 2, 3, 4, 5}.
- Пересечение множеств A и B (обозначается как A ∩ B) — результатом данной операции является множество, которое содержит все элементы, которые принадлежат как множеству A, так и множеству B. Например, если A = {1, 2, 3} и B = {3, 4, 5}, то A ∩ B = {3}.
- Разность множеств A и B (обозначается как A \ B) — результатом данной операции является множество, которое содержит все элементы, которые принадлежат множеству A, но не принадлежат множеству B. Например, если A = {1, 2, 3} и B = {3, 4, 5}, то A \ B = {1, 2}.
- Симметрическая разность множеств A и B (обозначается как A Δ B) — результатом данной операции является множество, которое содержит все элементы, которые принадлежат только одному из множеств A и B. Например, если A = {1, 2, 3} и B = {3, 4, 5}, то A Δ B = {1, 2, 4, 5}.
Операции над множествами позволяют решать различные задачи и проводить анализ данных. Они широко применяются в математике, логике, информатике и других науках.
Примеры дополнения множества

Рассмотрим несколько примеров дополнения множества:
1. Пусть есть два множества A = {1, 2, 3} и B = {2, 3, 4}. Дополнение множества A по отношению к множеству B будет содержать элементы, которые принадлежат множеству A, но не принадлежат множеству B. Таким образом, A \ B = {1}.
2. Рассмотрим множества C = {a, b, c} и D = {b, c, d}. Дополнение множества C по отношению к множеству D будет содержать элементы, которые принадлежат множеству C, но не принадлежат множеству D. Таким образом, C \ D = {a}.
3. Пусть есть множества E = {1, 2, 3, 4} и F = {3, 4, 5}. Дополнение множества E по отношению к множеству F будет содержать элементы, которые принадлежат множеству E, но не принадлежат множеству F. Таким образом, E \ F = {1, 2}.
Таким образом, дополнение множества позволяет выделить элементы, которые принадлежат одному множеству, но не принадлежат другому, и создать новое множество, состоящее только из этих элементов.
Дополнение пустого множества

Дополнение пустого множества определяется как разность универсального множества и пустого множества. Пустое множество не содержит ни одного элемента, поэтому его дополнение будет равно универсальному множеству.
Математически это можно записать следующим образом:
- Дополнение пустого множества: A\∅ = A
Таким образом, дополнение пустого множества не изменяет исходное множество. Это свойство дополнения пустого множества можно использовать при решении задач и доказательствах в математике.
Отображение дополнения множества на диаграмме Эйлера–Венна
Отображение дополнения множества на диаграмме Эйлера–Венна позволяет показать, какие элементы не входят в заданное множество. Обычно дополнение множества обозначается символом «¬».
На диаграмме Эйлера–Венна дополнение множества обозначается отдельной областью, расположенной вне границ основного множества. Эта область не пересекается с другими областями, представляющими другие множества.
Примером отображения дополнения множества на диаграмме Эйлера–Венна может служить следующая ситуация: есть множество всех животных и множество всех собак. Дополнение множества собак будет представлять собой область, которая не пересекается с областью, соответствующей множеству животных. Таким образом, на диаграмме Эйлера–Венна будет видно, что собаки не являются единственными животными.
Дополнение множества и теория вероятностей

В теории вероятностей, дополнение множества используется для определения вероятности события. Пусть S — пространство элементарных исходов, а A — некоторое событие. Тогда дополнением события A является событие, которое состоит из всех элементарных исходов пространства S, не входящих в событие A.
Дополнение множества можно определить с помощью различных операций над множествами. Например, если у нас есть универсальное множество U и множество A, то дополнение множества А можно определить как разность универсального множества и множества A, т.е. А’ = U \ A.
Дополнение множества в теории вероятностей имеет ряд важных свойств. В частности, вероятность события A и его дополнения A’ в сумме равна единице, т.е. P(A) + P(A’) = 1. Это свойство можно использовать для вычисления вероятности события, если мы знаем вероятность его дополнения.
Примером использования дополнения множества в теории вероятностей может служить задача о бросании игральной кости. Пусть S — пространство элементарных исходов, а A — событие, состоящее в выпадении четного числа. В этом случае, дополнение события A будет состоять из всех элементарных исходов, в которых выпадает нечетное число. Допустим, что вероятность события A равна 1/2. Тогда вероятность дополнения события A будет равна 1 — 1/2 = 1/2. Таким образом, вероятность выпадения нечетного числа также равна 1/2.
Таким образом, дополнение множества играет важную роль в теории вероятностей и позволяет определять вероятности событий на основе их дополнений.
Видео по теме:
Что такое дополнение множества?
Дополнение множества — это множество элементов, которые не принадлежат данному множеству. Другими словами, это все элементы, которые отсутствуют в данном множестве.
Как обозначается дополнение множества?
Дополнение множества обозначается символом «A'». То есть, если A — исходное множество, то A’ — его дополнение.
Как использовать дополнение множества в математике?
Дополнение множества используется для определения отсутствующих элементов и установления связей между различными множествами. Оно позволяет решать задачи по поиску недостающих элементов и анализу включения множеств.
Что такое дополнение множества?
Дополнением множества A называется множество элементов, которые не принадлежат множеству A. Обозначается A’ или Ac.




В статье очень хорошо разобрана тема дополнения множеств в математике. Мне понравилось, как автор описал определение и свойства этого оператора. Благодаря этому я лучше понял, как работает дополнение и какие операции можно выполнять с множествами. Также автор предложил несколько примеров, которые помогли мне усвоить материал. Особенно интересным был пример с двумя множествами и их дополнением. Я узнал, что дополнение множества состоит из всех элементов, которые не входят в само множество. Это очень полезное свойство, которое можно применять в различных задачах. Очень рад, что нашел эту статью. Она помогла мне разобраться в теме дополнения множеств и улучшить свои знания в математике. Большое спасибо автору за доступное изложение материала и хорошие примеры!
Дополнение множеств в математике — это очень интересная и полезная тема! Я всегда стремлюсь расширять свои знания в этой области, поэтому статья на эту тему была для меня очень полезной. Определение дополнения множества позволяет нам выделить элементы, которые не входят в исходное множество. Обозначается это так: если у нас есть множество А, то его дополнение обозначается как А с чертой сверху. Например, если А — множество всех четных чисел, то А’ будет представлять собой множество всех нечетных чисел. Одно из самых важных свойств дополнения множества — это то, что оно является коммутативным. Это означает, что порядок, в котором мы берем дополнение множества, не влияет на результат. Например, дополнение дополнения множества А будет равно самому множеству А. Это свойство очень полезно при решении различных задач и позволяет нам использовать дополнение множества в различных математических операциях. Примеры использования дополнения множества в математике встречаются повсюду. Например, в теории вероятностей мы часто используем дополнение множества событий. Если у нас есть множество всех возможных исходов эксперимента, то дополнение этого множества будет представлять собой множество всех невозможных исходов. Это позволяет нам решать задачи вероятности и вычислять вероятности различных событий. В общем, дополнение множества — это очень полезное понятие в математике, которое позволяет нам анализировать и решать различные задачи. Я очень рада, что узнала больше об этом и смогла применить эти знания на практике. Спасибо за статью!
Статья очень понравилась! Она очень доступно и ясно объясняет основные понятия и свойства дополнения множеств в математике. Я всегда интересуюсь математикой и стараюсь углублять свои знания в этой области. Изучение дополнения множеств помогает лучше понять взаимодействие элементов внутри множества и внешние отношения с другими множествами. Основное определение, которое было приведено в статье, очень простое и понятное: дополнение множества А относительно универсального множества U – это множество всех элементов, которые не принадлежат множеству А, но принадлежат универсальному множеству U. Также в статье были приведены основные свойства дополнения множеств, которые помогают в дальнейшем использовании этого понятия. Мне было интересно узнать о том, что дополнение множества является коммутативным и ассоциативным оператором. Это позволяет свободно менять порядок множеств и применять операцию дополнения множества к нескольким множествам одновременно. Например, если у нас есть множества А, В и С, то (А ∪ В) ∪ С = А ∪ (В ∪ С), что очень удобно при работе с большими объемами данных. Также в статье были приведены примеры использования дополнения множеств в математике. Например, это может быть полезно при решении задач на пересечение и объединение множеств, на выделение общих и уникальных элементов. Было бы интересно узнать больше примеров, чтобы лучше понять, как это применяется на практике. В целом, статья очень полезная и информативная. Она помогла мне лучше понять суть дополнения множеств и его применение в математике. Я буду продолжать изучать эту тему, чтобы лучше разбираться в математических операциях и взаимодействии множеств. Большое спасибо автору за такую интересную статью!