Что такое универсальное множество в математике

Универсальное множество в математике — это множество, которое содержит все элементы или объекты, которые рассматриваются в данной области математики. В теории множеств, универсальное множество является основным понятием, которое помогает определить свойства других множеств и отношений между ними. Универсальное множество играет важную роль в различных областях математики, таких как логика, топология и алгебра.

В математике существует понятие универсального множества, которое играет важную роль в различных областях этой науки. Универсальное множество – это множество, которое включает в себя все возможные элементы или объекты, рассматриваемые в данной области. Оно является базовым для определения других множеств и позволяет проводить различные математические операции.

Универсальное множество обычно обозначается символом U. Оно может быть конечным или бесконечным, в зависимости от контекста задачи. Например, в теории множеств универсальным множеством может быть множество всех натуральных чисел, всех действительных чисел или всех точек на плоскости.

Одним из свойств универсального множества является то, что оно содержит все элементы, принадлежащие другим множествам. Также универсальное множество может быть использовано для определения операций объединения, пересечения и разности множеств. Например, объединение двух множеств будет содержать все элементы, принадлежащие хотя бы одному из них, а пересечение – только общие элементы.

Примером универсального множества может служить множество всех людей на планете Земля. В этом случае оно будет включать в себя каждого отдельного человека, который существует или когда-либо существовал. Таким образом, универсальное множество людей может быть использовано для определения любого другого множества, например, множества всех женщин, всех детей или всех людей, страдающих определенным заболеванием.

В заключение, универсальное множество является важным понятием в математике, которое позволяет определять и проводить различные операции с другими множествами. Оно обладает свойством содержать все возможные элементы, рассматриваемые в данной области. Примеры универсальных множеств могут быть разными в зависимости от контекста задачи, но они всегда играют важную роль в математическом анализе и решении различных задач.

Что такое универсальное множество

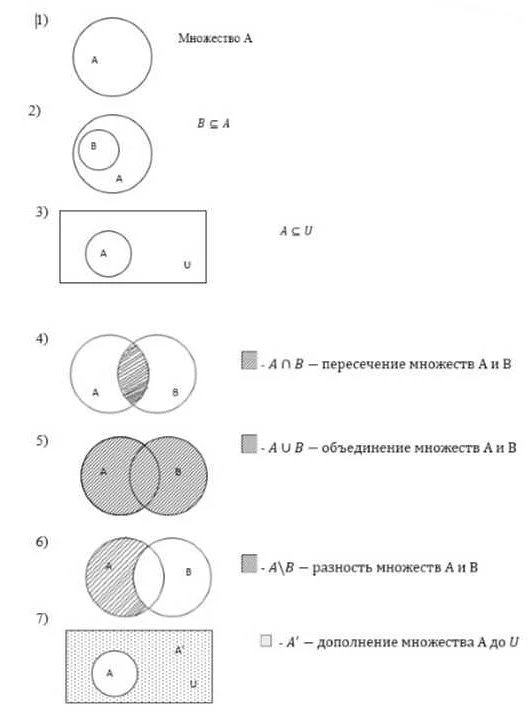
Универсальное множество обычно обозначается символом U. Оно может быть бесконечным или конечным, в зависимости от контекста и рассматриваемой системы.

Примером универсального множества может служить множество всех натуральных чисел, обозначаемое как N. В этом случае, N является универсальным множеством для всех натуральных чисел.

Универсальное множество имеет ряд свойств:

1. Любое множество может быть подмножеством универсального множества.
2. Универсальное множество не может быть подмножеством другого множества.
3. Универсальное множество содержит все возможные элементы, представленные в данной системе.
4. Универсальное множество является основой для определения операций и свойств других множеств.

Универсальное множество играет важную роль в математике, так как позволяет строить и анализировать различные структуры и отношения между элементами.

Основные определения и термины

Элемент — отдельный объект, принадлежащий множеству. Элементы могут быть различными по своим свойствам и признакам.

Подмножество — множество, элементы которого являются также элементами другого множества. Формально, множество A является подмножеством множества B, если каждый элемент A также является элементом B.

Декартово произведение — множество, состоящее из всех возможных упорядоченных пар элементов из двух множеств. Например, для множеств A = {1, 2} и B = {a, b} декартово произведение A × B = {(1, a), (1, b), (2, a), (2, b)}.

Пересечение — операция над множествами, результатом которой является множество, содержащее только те элементы, которые принадлежат обоим исходным множествам.

Объединение — операция над множествами, результатом которой является множество, содержащее все элементы, которые принадлежат хотя бы одному из исходных множеств.

Разность — операция над множествами, результатом которой является множество, содержащее только те элементы, которые принадлежат первому исходному множеству, но не принадлежат второму исходному множеству.

Дополнение — операция над множеством, результатом которой является множество, содержащее все элементы универсального множества, которые не принадлежат исходному множеству.

Мощность — количество элементов в множестве. Обычно обозначается символом |A|, где A — множество.

Примеры универсальных множеств

1. Множество всех натуральных чисел:

Множество натуральных чисел обозначается как N и содержит все положительные целые числа, начиная с 1. Все остальные множества чисел, такие как целые, рациональные и действительные числа, являются подмножествами множества натуральных чисел. Поэтому множество натуральных чисел является универсальным множеством для всех этих числовых систем.

2. Множество всех точек на плоскости:

Множество всех точек на плоскости, которое обозначается как P, является универсальным множеством для геометрии. Оно содержит все возможные точки на плоскости, включая точки с целочисленными координатами, точки с десятичными координатами и другие.

3. Множество всех слов:

Множество всех слов, которое обозначается как W, является универсальным множеством для языков и лингвистики. Оно содержит все возможные слова, которые можно образовать из различных букв и символов.

Эти примеры показывают, что универсальные множества играют важную роль в математике и других науках, предоставляя полный набор элементов для исследования и анализа.

Свойства универсальных множеств

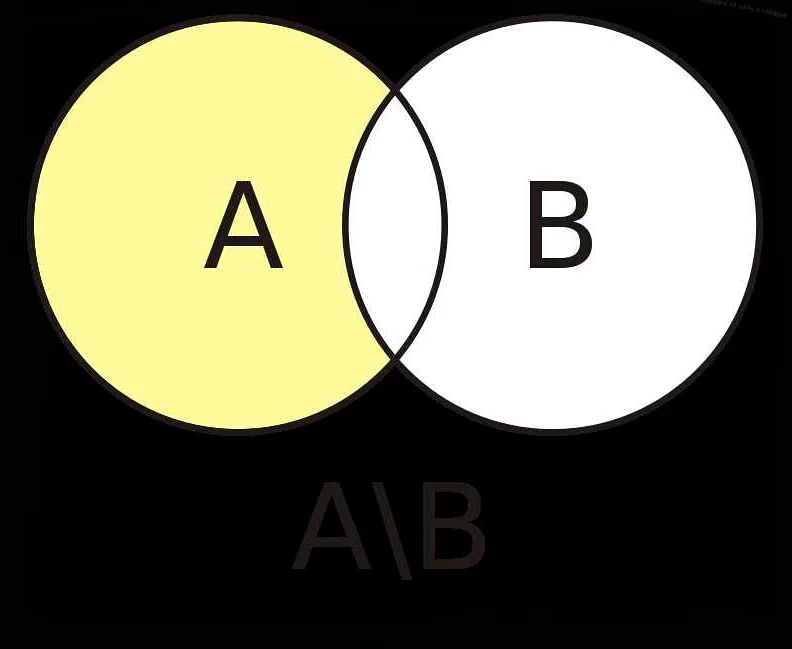
1. Включение всех элементов:

Универсальное множество содержит все возможные элементы, которые могут быть включены в другие множества. То есть, любой элемент из других множеств также будет принадлежать универсальному множеству.

2. Сохранение свойств:

Если какое-либо свойство верно для всех элементов из других множеств, то оно также будет верно для всех элементов универсального множества. Например, если все элементы множества A обладают свойством P, то все элементы универсального множества также будут обладать этим свойством.

3. Существование пустого множества:

Универсальное множество может содержать пустое множество, то есть множество, не содержащее ни одного элемента. Пустое множество является подмножеством всех множеств, включая универсальное множество.

4. Отсутствие объединения:

Универсальное множество не может быть объединено с другими множествами, так как оно уже содержит все возможные элементы. Поэтому, объединение универсального множества с другим множеством будет равно самому универсальному множеству.

5. Существование пересечения:

Универсальное множество может иметь пересечение с другими множествами. Пересечение универсального множества с другим множеством будет равно самому другому множеству, так как все элементы универсального множества также принадлежат этому другому множеству.

6. Связь с дополнением:

Дополнение универсального множества является пустым множеством, так как универсальное множество содержит все возможные элементы. Поэтому, дополнение универсального множества к любому другому множеству будет равно дополнению этого другого множества.

7. Единственность:

Универсальное множество является единственным, то есть для любых двух универсальных множеств верно, что они равны друг другу. Это свойство следует из включения всех элементов и отсутствия объединения универсального множества с другими множествами.

Таким образом, универсальное множество обладает рядом особых свойств, которые делают его важным понятием в математике.

Применение универсальных множеств

Одним из основных применений универсальных множеств является построение алгоритмов и структур данных. Универсальные множества позволяют эффективно решать задачи, связанные с поиском элементов, проверкой наличия элемента в множестве и другими операциями.

В теории графов универсальные множества используются для описания свойств и характеристик графов. Например, универсальное множество вершин графа может помочь в определении его свойств, таких как связность, цикличность и планарность.

Универсальные множества также активно применяются в теории вероятностей и статистике. Они позволяют моделировать случайные процессы и проводить статистические исследования с использованием больших объемов данных.

Кроме того, универсальные множества имеют важное значение в теории формальных языков и автоматов. Они используются для описания и анализа языковой грамматики, построения и применения лексических и синтаксических анализаторов.

В области искусственного интеллекта и машинного обучения универсальные множества применяются для описания и представления знаний. Они позволяют компьютерным системам эффективно обрабатывать и хранить большие объемы информации.

Таким образом, универсальные множества играют важную роль в различных областях математики и информатики, обеспечивая эффективное решение задач и развитие новых методов и технологий.

Вопрос-ответ:

Что такое универсальное множество в математике?

Универсальное множество — это множество, которое содержит все элементы других множеств, рассматриваемых в определенном контексте. Оно может быть использовано для описания всех возможных объектов данного типа.

Какие примеры универсальных множеств в математике можно привести?

Один из примеров универсального множества — множество всех натуральных чисел. Оно содержит все натуральные числа и может быть использовано для описания любого натурального числа. Еще один пример — множество всех булевых функций, которое содержит все возможные комбинации значений истинности и может быть использовано для описания любой булевой функции.

Какие свойства имеет универсальное множество?

Универсальное множество должно содержать все элементы других множеств, которые рассматриваются в определенном контексте. Оно также должно быть достаточно большим, чтобы включать все возможные объекты данного типа. При этом универсальное множество может быть бесконечным.

Как универсальное множество используется в математике?

Универсальное множество может быть использовано для описания и классификации объектов данного типа. Оно может также быть использовано для доказательства существования или невозможности определенных свойств или объектов. Универсальное множество является важным инструментом в математике и используется в различных областях, таких как логика, теория множеств и алгебра.

Как определить универсальное множество в конкретной области математики?

Определение универсального множества зависит от конкретной области математики, в которой оно используется. Для определения универсального множества необходимо учесть особенности и требования данной области. Например, в теории множеств универсальное множество может быть определено как множество всех объектов, которые можно рассматривать в данной теории.

Что такое универсальное множество в математике?

Универсальное множество в математике — это множество, которое содержит все возможные элементы, рассматриваемые в данной области математики. Оно является неким «универсальным» набором, в котором можно представить все элементы, используемые в рассматриваемой области.

Связь с другими понятиями в математике

Универсальное множество в математике тесно связано с другими понятиями и концепциями, которые играют важную роль в различных областях математики. Ниже приведены несколько примеров таких связей:

ПонятиеОписаниеСвязь с универсальным множеством

Пустое множество	Множество, не содержащее ни одного элемента	Универсальное множество может включать пустое множество как подмножество
Подмножество	Множество, элементы которого являются также элементами другого множества	Универсальное множество может содержать в себе все подмножества
Пересечение множеств	Множество, содержащее элементы, которые принадлежат одновременно двум или более множествам	Универсальное множество может содеражть пересечение всех возможных множеств
Объединение множеств	Множество, содержащее все элементы из двух или более множеств	Универсальное множество может содержать объединение всех возможных множеств
Дополнение множества	Множество, содержащее элементы, не принадлежащие данному множеству	Универсальное множество может быть использовано для определения дополнения

Это лишь некоторые из примеров связей универсального множества с другими понятиями в математике. Универсальное множество является важным инструментом, позволяющим анализировать и изучать другие множества и их свойства.

Видео по теме: