Раскройте суть математического понятия функция что такое аргумент функции какие функции вы знаете

Функция в математике — это основное понятие, определяющее зависимость одной величины от другой. Аргумент функции — это независимая переменная, от которой зависит значение функции. В статье рассмотрены основные типы функций и приведены примеры известных функций. Узнайте больше о функциях и их аргументах в математике.

Функция — одно из основных понятий математики, которое широко используется в различных областях науки и практических приложениях. Она представляет собой зависимость между двумя множествами, называемыми областью определения и областью значений. Математически функцию можно представить в виде графика, где по оси абсцисс откладываются значения аргументов, а по оси ординат — соответствующие значения функции.

Аргументы функции — это значения, которые подставляются в функцию, чтобы получить соответствующие значения функции. В зависимости от типа функции, аргументы могут быть числами, точками или другими объектами. Количество аргументов может быть разным: от одного до нескольких. Например, в функции с одним аргументом, значение функции зависит только от этого аргумента, а в функции с двумя аргументами, значение функции зависит от обоих аргументов.

Существует множество видов функций, каждый из которых имеет свои особенности и применение. Одной из самых простых и широко используемых функций является линейная функция. Она задается уравнением вида y = kx + b, где k и b — константы, определяющие наклон и смещение графика функции.

Квадратичная функция — это функция вида y = ax^2 + bx + c, где a, b и c — коэффициенты, определяющие форму и положение графика функции. Квадратичные функции широко применяются в физике, экономике и других науках для моделирования различных явлений и процессов.

Тригонометрические функции — это функции, которые связаны с геометрическими свойствами треугольников и окружностей. Они включают такие функции, как синус, косинус и тангенс. Тригонометрические функции активно используются в физике, геометрии и других науках для решения различных задач и моделирования физических явлений.

В данной статье мы рассмотрим основные понятия функции, ее аргументы и наиболее популярные виды функций, а также их применение в различных областях науки и практики.

Функция в математике: суть и аргументы

Аргументы функции — это входные значения, которые подставляются в функцию для вычисления соответствующего значения функции. Аргументы могут быть числами, переменными или состоять из более сложных выражений. Значения функции — это результаты вычисления функции для заданных аргументов. Значения функции могут быть числами, переменными или состоять из более сложных выражений.

Примеры популярных видов функций:

Вид функцииОписание

Линейная функция	Функция вида y = kx + b, где k и b — постоянные значения
Квадратичная функция	Функция вида y = ax^2 + bx + c, где a, b и c — постоянные значения
Тригонометрическая функция	Функция, которая зависит от угла, такие как синус, косинус, тангенс и другие
Логарифмическая функция	Функция вида y = log_b(x), где b — основание логарифма
Экспоненциальная функция	Функция вида y = a^x, где a — постоянное значение

Что такое функция в математике?

Функция состоит из двух частей: множества аргументов (входных данных) и множества значений (выходных данных). При этом каждому аргументу соответствует только одно значение. Функцию обычно обозначают символом f и записывают в виде f(x), где x – аргумент функции.

Функции делятся на различные типы в зависимости от их свойств и способа задания. Некоторые из наиболее популярных видов функций включают в себя:

• Линейные функции, которые представляют собой прямую линию на графике. Они имеют вид f(x) = ax + b, где a и b – константы.
• Квадратичные функции, которые имеют формулу f(x) = ax^2 + bx + c, где a, b и c – константы.
• Степенные функции, которые имеют вид f(x) = x^n, где n – степень.
• Тригонометрические функции, такие как синус, косинус и тангенс, которые описывают зависимость между углом и соотношением сторон в треугольнике.
• Логарифмические функции, которые представляют собой обратные операции к экспоненциальным функциям и имеют вид f(x) = log_a(x), где a – основание логарифма.

Функции играют важную роль в математике и имеют широкий спектр применений в науке, технике, экономике и других областях. Они позволяют моделировать и анализировать различные явления и процессы, а также решать разнообразные задачи.

Составные элементы функции

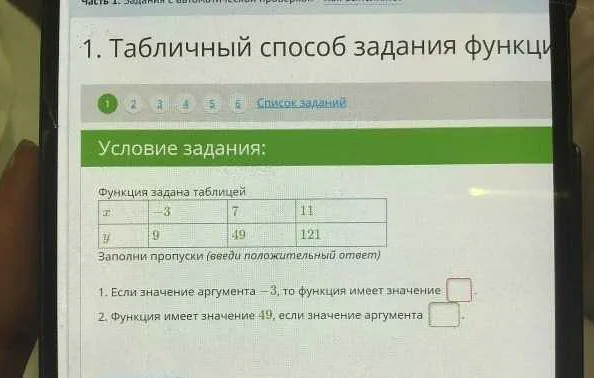
Функция в математике состоит из нескольких важных элементов, которые определяют ее суть и свойства. Вот основные составные элементы функции:

1. Область определения (ОО) функции: это множество всех возможных значений аргумента функции, при которых функция определена и имеет смысл. Область определения может быть задана явно или определиться из контекста задачи.

2. Область значений (ОЗ) функции: это множество всех возможных значений функции, которые она может принимать при выборе аргументов из ее области определения. Область значений может быть задана явно или определиться из контекста задачи.

3. График функции: это геометрическое представление функции на координатной плоскости. График функции представляет собой множество точек (x, y), где x — значение аргумента функции, y — значение функции при данном аргументе.

4. Зависимость: функция описывает зависимость между аргументом и значением функции. В зависимости от вида функции, эта зависимость может быть линейной, квадратичной, экспоненциальной и т. д.

Каждый из этих элементов является важной частью функции и помогает понять ее свойства и особенности. Изучение составных элементов функции позволяет решать различные математические задачи и применять функции в различных областях науки и техники.

Аргументы функции и их роль

Аргументы функции могут быть любого типа данных: числа, строки, списки, объекты и т.д. Количество аргументов может также варьироваться в зависимости от конкретной функции.

АргументОписание

ar1, ar2, …, arn

Аргументы функции, передаваемые в виде отдельных значений или переменных.

Аргументы функции могут использоваться для передачи данных извне внутрь функции, а также для обеспечения гибкости и переиспользования кода. Они позволяют задавать различные входные значения, влияющие на результат работы функции.

В ходе выполнения функции аргументы могут использоваться внутри функции для выполнения определенных операций или для принятия решений на основе переданных значений.

Например, функция, вычисляющая сумму двух чисел, может иметь два аргумента — числа, которые нужно сложить. А функция, проверяющая, является ли число четным, может иметь один аргумент — число, которое нужно проверить.

Правильное использование аргументов функции позволяет создавать более универсальные и гибкие программы, которые могут выполнять различные задачи в зависимости от переданных значений.

Значение функции и его зависимость от аргумента

Значение функции зависит от ее аргумента, который является входным параметром функции. Аргумент может быть любым элементом из области определения функции. При заданных аргументах функция возвращает соответствующее значение из области значений.

Зависимость между значением функции и ее аргументом может быть представлена в виде графика. На графике аргумент обычно откладывается по горизонтальной оси, а соответствующие значения функции — по вертикальной оси. График функции позволяет визуально представить изменение значения функции при изменении аргумента.

Важно отметить, что одному аргументу может соответствовать только одно значение функции. Это свойство называется однозначностью функции. Если функция принимает несколько значений для одного аргумента, то она считается неоднозначной.

Кроме того, функция может быть задана аналитически, то есть с помощью формулы или алгоритма, или же графически, с помощью графика или таблицы значений. В любом случае, значение функции всегда зависит от ее аргумента и может быть определено для любого значения аргумента из области определения функции.

Популярные виды функций

Линейная функция: Линейная функция представляет собой функцию вида f(x) = ax + b, где a и b — константы. График линейной функции представляет собой прямую линию, которая имеет одинаковый наклон и не меняет своего направления.

Квадратичная функция: Квадратичная функция представляет собой функцию вида f(x) = ax^2 + bx + c, где a, b и c — константы. График квадратичной функции представляет собой параболу, которая может быть направленной вверх или вниз в зависимости от значения коэффициента a.

Экспоненциальная функция: Экспоненциальная функция представляет собой функцию вида f(x) = a^x, где a — константа. График экспоненциальной функции имеет форму плавно возрастающей или убывающей кривой.

Логарифмическая функция: Логарифмическая функция представляет собой функцию вида f(x) = logₐ(x), где a — константа. Логарифмическая функция является обратной функцией к экспоненциальной функции и имеет график, который является отражением графика экспоненциальной функции относительно прямой y = x.

Тригонометрическая функция: Тригонометрическая функция представляет собой функцию, которая отображает угол в соответствующее значение тригонометрической функции (синус, косинус, тангенс и т.д.). Тригонометрические функции широко используются в геометрии, физике и других науках.

Линейная функция

Линейная функция имеет вид y = mx + b, где m и b — это константы, а x — это независимая переменная.

Коэффициент m называется наклоном (или угловым коэффициентом) линейной функции. Он определяет угол наклона прямой линии. Если m положительный, то линия наклонена вверх, если m отрицательный, то линия наклонена вниз.

Коэффициент b называется свободным членом. Он определяет точку пересечения линии с осью y (ось ординат).

Линейные функции широко используются в различных областях, таких как физика, экономика, статистика и т. д. Они позволяют моделировать простые и прямолинейные зависимости между переменными.

Примеры линейных функций:

• y = 2x + 3
• y = -0.5x + 2
• y = 4x — 1

Графики линейных функций представляют собой прямые линии на координатной плоскости, которые можно нарисовать, зная две точки или наклон и точку пересечения с осью y.

Линейные функции являются основой для изучения более сложных типов функций и позволяют понять базовые понятия и свойства функций в математике.

Квадратическая функция

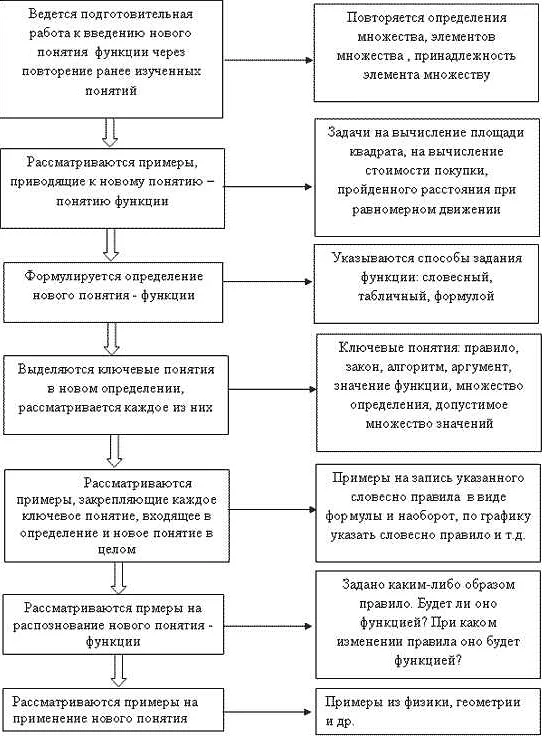
f(x) = ax^2 + bx + c,

где a, b и c – числа, причем a ≠ 0.

График квадратической функции представляет собой параболу, которая может быть направленной вверх или вниз, в зависимости от значения коэффициента a. Если a > 0, то парабола направлена вверх, если a < 0, то парабола направлена вниз.

Вершина параболы – это точка, в которой график квадратической функции достигает экстремального значения. Координаты вершины можно найти с помощью формулы:

x = -b / (2a),

y = f(x).

Квадратическая функция имеет много применений в различных областях науки и техники. Например, она используется для моделирования траектории движения тела под действием силы тяжести, расчета максимальной или минимальной стоимости в задачах экономики, определения оптимальных параметров в задачах оптимизации и т.д.

Некоторые известные примеры квадратических функций:

• Парабола y = x^2 – график простейшей квадратической функции;
• Парабола y = -x^2 – парабола, направленная вниз;
• Парабола y = 2x^2 – парабола, направленная вверх, с коэффициентом «растяжения» 2;
• Парабола y = (x-1)^2 – парабола, смещенная на 1 единицу вправо;
• Парабола y = x^2 + 2x + 1 – парабола, с коэффициентами a, b и c, отличными от 1.

Степенная функция

Степенные функции имеют важное значение в математике и естественных науках. Их графики могут иметь различные формы, в зависимости от значений коэффициента и показателя степени. Например, при n = 1 график будет представлять прямую линию, называемую линейной функцией. При n = 2 график будет представлять параболу, при n = 3 — кубическую кривую, и так далее.

Степенные функции широко используются для моделирования различных явлений в физике, экономике, биологии и других областях. Они помогают описывать зависимость между различными переменными и предсказывать поведение системы.

Тригонометрическая функция

Существует несколько популярных видов тригонометрических функций:

• Синус (sin): отношение противоположной стороны к гипотенузе
• Косинус (cos): отношение прилежащей стороны к гипотенузе
• Тангенс (tg): отношение противоположной стороны к прилежащей стороне
• Котангенс (ctg): отношение прилежащей стороны к противоположной стороне
• Секанс (sec): отношение гипотенузы к прилежащей стороне
• Косеканс (cosec): отношение гипотенузы к противоположной стороне

Тригонометрические функции находят широкое применение в различных областях науки и техники, таких как физика, инженерия, компьютерная графика и др.

Вопрос-ответ:

Что такое функция в математике?

Функция в математике — это соответствие между двумя множествами, где каждому элементу из первого множества сопоставляется ровно один элемент из второго множества. Функция определяет зависимость между этими элементами и может быть представлена графически или аналитически.

Какие аргументы может принимать функция?

Функция может принимать различные аргументы, в зависимости от своего определения. Аргумент — это значение, на которое мы хотим подставить в функцию и получить соответствующее значение из области значений функции. Например, в функции y = f(x), аргументом является x.

Какие виды функций являются наиболее популярными?

Существует множество видов функций, но некоторые из наиболее популярных включают линейные функции, квадратичные функции, экспоненциальные функции, логарифмические функции и тригонометрические функции. Они широко применяются в различных областях математики, физики, экономики, и т.д.

Какие свойства имеют функции в математике?

Функции в математике обладают несколькими свойствами. Одно из них — уникальность значений, то есть каждому значению аргумента соответствует только одно значение функции. Кроме того, функции могут быть определены на определенных областях значений и аргументов, и они могут быть определены как аналитически, так и графически.

Видео по теме: