Что такое ядра в математике

Ядра в математике — это понятие, используемое для описания основных элементов структуры или операции. Узнайте, как ядра применяются в различных областях математики и как они помогают в понимании сложных концепций и проблем.

Ядра — это важное понятие в математике, которое находит применение во многих областях, включая алгебру, теорию вероятностей и математическую физику. Ядро — это особый тип отображения между двумя множествами, обладающее некоторыми свойствами.

Самое главное свойство ядер — сохранение информации. Они образуют отображение, сохраняющее «ядро» информации из начального множества в конечное множество. Таким образом, они играют важную роль в сжатии информации, фильтрации шума и обработке данных в различных приложениях.

Кроме того, ядра имеют ряд других важных свойств. Они могут быть симметричными, ассоциативными и удовлетворять другим алгебраическим законам. Они также могут быть комбинированы с другими ядрами, образуя новые ядра с помощью операций, таких как сумма, умножение и свертка.

Примером ядра может служить ядро Гаусса, которое широко применяется в обработке изображений. Это ядро позволяет размыть изображение, устраняя шум и несовершенства, сохраняя при этом основные детали и структуру изображения.

В заключение, ядра — это важное понятие в математике, которое используется для обработки информации, фильтрации шума и многих других задач. Они обладают свойством сохранения информации и могут быть комбинированы с другими ядрами, создавая новые ядра с помощью различных операций. Ядро Гаусса является примером популярного ядра, используемого в обработке изображений.

Что такое ядра в математике?

Ядро функции можно представить как множество всех входных значений, которые переходят в ноль после применения функции. Если функция представлена уравнением, то ядро может быть найдено путем решения уравнения с нулевой правой частью.

Важным свойством ядра является его замкнутость относительно операций, определенных над элементами исходного множества. Это означает, что если два элемента принадлежат ядру, то их сумма и произведение также принадлежат ядру.

Примеры ядер в математике включают нулевое ядро линейного отображения, нулевое ядро абелевой группы и ядро сопряжения в групповом гомоморфизме.

Видео по теме:

Основные свойства ядер

2. Непустота: Ядро множества всегда содержит хотя бы один элемент. Если A — непустое множество, то его ядро также непусто.

3. Единственность: У каждого множества может быть только одно ядро. Если существуют два различных ядра A и B, то B содержится в A, и наоборот.

4. Идемпотентность: Ядро множества является идемпотентным оператором, то есть применение ядра к самому себе не меняет результат. Если A — множество и K — его ядро, то ядро ядра A равно ядру A, т.е. K(K(A)) = K(A).

5. Монотонность: Ядро монотонно, то есть если A и B — множества, причем А содержится в B, то ядро A содержится в ядре B. То есть, если A ⊆ B, то K(A) ⊆ K(B).

6. Сохранение пересечений: Ядро сохраняет пересечение множеств. То есть, если A и B — множества, то ядро их пересечения равно пересечению их ядер, т.е. K(A ∩ B) = K(A) ∩ K(B).

7. Сохранение объединений: Ядро сохраняет объединение множеств. То есть, если A и B — множества, то ядро их объединения содержится в объединении их ядер, т.е. K(A ∪ B) ⊆ K(A) ∪ K(B).

8. Сохранение разности: Ядро сохраняет разность множеств. То есть, если A и B — множества, то ядро разности A и B содержится в разности ядер A и B, т.е. K(A \ B) ⊆ K(A) \ K(B).

Примеры ядер в математике

Ядра в математике широко применяются в различных областях, включая линейную алгебру, функциональный анализ, теорию графов и другие.

Ниже приведены некоторые примеры ядер:

1. Ядро Гаусса: это одно из самых распространенных ядер, используемых в машинном обучении. Оно широко применяется для решения задач классификации и регрессии.

2. Ядро Полинома: это ядро, которое применяется для обработки данных, имеющих нелинейную структуру. Оно позволяет создавать нелинейные модели и использовать их для решения различных задач.

3. Ядро Сигмоиды: это ядро, которое применяется в некоторых моделях машинного обучения, таких как нейронные сети. Оно помогает модели улавливать нелинейные зависимости в данных.

4. Ядро Лапласа: это ядро, которое применяется в анализе текстов и изображений. Оно позволяет выделить существенные особенности данных.

5. Ядро Хи-квадрат: это ядро, которое применяется для оценки расстояния между распределениями вероятности. Оно используется в статистике и машинном обучении.

Это лишь некоторые из множества ядер, которые используются в математике. Каждое ядро имеет свои особенности и применяется в определенных областях.

Вопрос-ответ:

Что такое ядра в математике?

Ядра в математике — это понятие из области алгебры, которое используется для описания отображений между алгебраическими структурами. Ядро отображения определяется как множество элементов, которые переходят в нейтральный элемент в области значений.

Какие свойства имеют ядра в математике?

Ядра обладают несколькими важными свойствами. Во-первых, они всегда являются подгруппами в группе области определения отображения. Во-вторых, они имеют непустое пересечение с образом отображения. В-третьих, ядра сохраняют операции и преобразуют нейтральный элемент в нейтральный элемент.

Как можно найти ядра отображения?

Для нахождения ядра отображения нужно решить уравнение f(x) = e, где f — отображение, x — неизвестная переменная, e — нейтральный элемент в области значений отображения. Решение этого уравнения даст множество элементов, которые являются ядром отображения.

Можете привести примеры ядер в математике?

Конечные абелевы группы имеют тривиальное ядро, так как отображение на них всегда инъективно. Другой пример — ядро гомоморфизма колец, где отображение переводит ноль в ноль. Также ядра могут быть использованы для определения ядерных множеств в теории меры и интеграла.

Какие приложения имеют ядра в математике?

Ядра широко применяются в различных областях математики и физики. Например, они используются для изучения симметрий и пространственной структуры материалов в теории групп и алгебры. Также ядра находят применение в анализе данных, машинном обучении и компьютерном зрении для выделения ключевых признаков и уменьшения размерности данных.

Ядра в теории групп

Формально, ядро группы G определяется следующим образом:

• Ядро группы G обозначается как ker(G) или Ker(G).
• Ядро G состоит из элементов g из G таких, что g * e = e * g = e, где e — единичный элемент группы G.
• Ядро G является подгруппой G.

Свойства ядра в теории групп:

1. Ядро группы G всегда нормальная подгруппа G.
2. Если ядро группы G состоит только из единичного элемента, то группа G является простой группой.
3. Ядро группы G является тривиальной подгруппой тогда и только тогда, когда группа G является абелевой.
4. Ядро группы G является самой большой подгруппой G, в которой все элементы переводят единичный элемент в единичный элемент.

Примеры ядер в теории групп:

• Ядро гомоморфизма группы G в группу H является подгруппой G, состоящей из элементов, которые переводятся гомоморфизмом в единичный элемент группы H.
• Ядро группы автоморфизмов группы G является подгруппой G, состоящей из элементов, которые являются тождественными автоморфизмами.

Ядра в теории графов

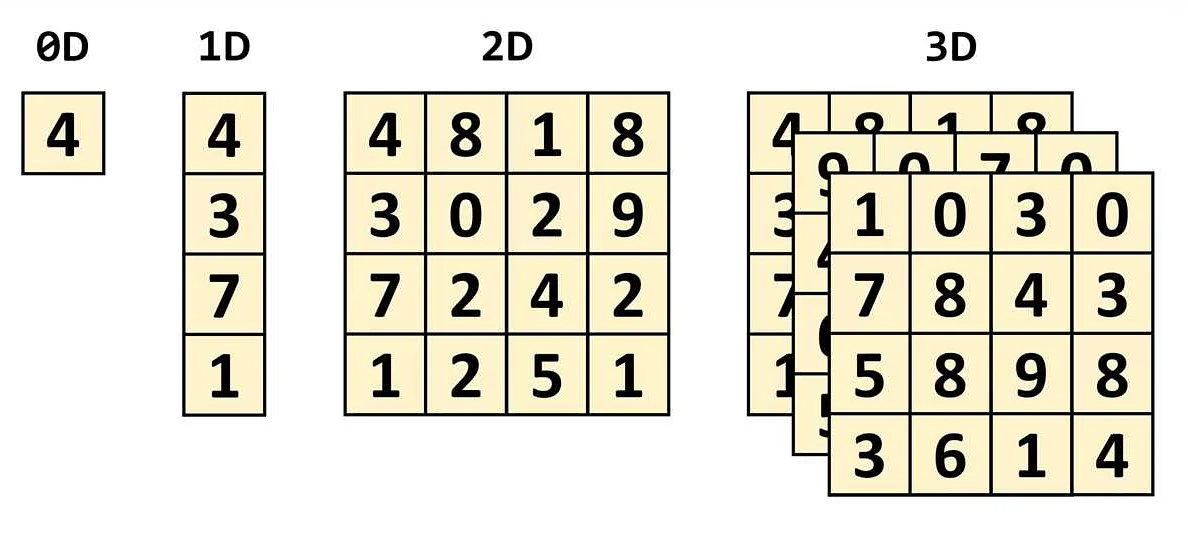
В теории графов ядром называется подмножество вершин графа, в котором для каждой вершины существует ребро, связывающее ее с любой другой вершиной ядра. Ядро представляет собой максимальное по размеру независимое множество вершин графа.

Ядра в теории графов имеют несколько свойств:

1. Ядро является независимым множеством вершин графа. Это означает, что никакие две вершины из ядра не соединены ребром.
2. Ядро является максимальным по размеру независимым множеством вершин графа. Это означает, что нельзя добавить в ядро еще одну вершину так, чтобы оно осталось независимым.
3. Все вершины графа, не входящие в ядро, имеют хотя бы одно ребро, соединяющее их с вершиной из ядра. Иначе говоря, ядро является связанным с остальным графом.
4. Ядро может быть найдено с помощью алгоритма поиска максимального независимого множества графа.

Примером графа с ядром может служить граф, состоящий из вершин, представляющих людей, и ребер, представляющих знакомство между людьми. Ядром в таком графе будет максимальное независимое множество людей, где каждый человек знаком со всеми остальными.

Ядра в теории функций

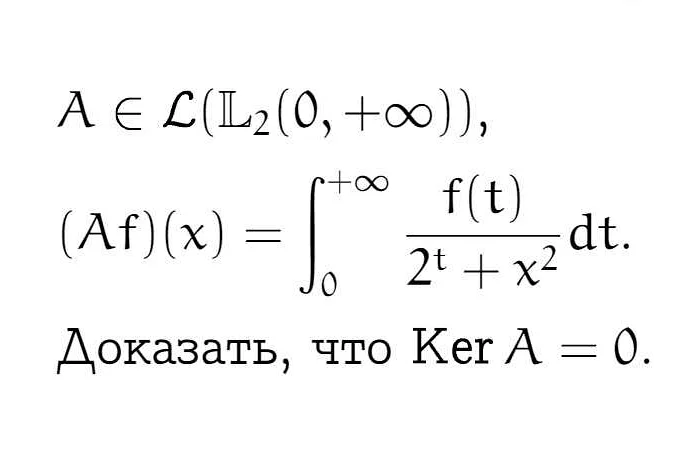
Ядро функции может иметь разные свойства, такие как симметрия, положительность, интегрируемость и др. От свойств ядра функции зависит его роль в теории функций и его применение в конкретных задачах.

Примером ядра функции может служить интегральное ядро, которое возникает в решении различных интегральных уравнений. Интегральное ядро обычно содержит информацию о взаимодействии между переменными в пределах определенной области или на заданной сетке.

Ядра функций часто используются для описания различных физических явлений, таких как теплопроводность, диффузия, взаимодействие частиц и др. Они также широко применяются в математическом анализе, численных методах и статистике.

Изучение ядер функций позволяет лучше понять взаимосвязь между переменными и описать сложные математические и физические процессы с помощью простых и компактных выражений.

Ядра в анализе данных

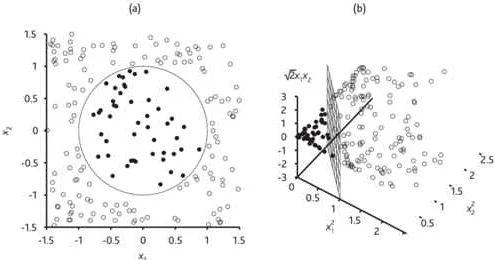
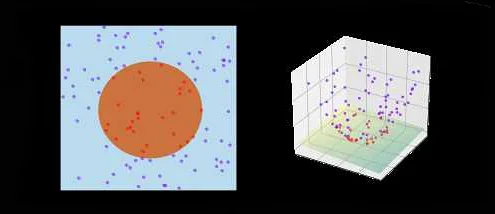
Ядра, или ядерные функции, играют важную роль в анализе данных. Они используются для выполнения различных операций, таких как уменьшение размерности данных, извлечение признаков и кластеризация.

Одним из применений ядер в анализе данных является метод главных компонент (PCA). PCA позволяет снизить размерность данных, сохраняя важные статистические свойства. Ядерная PCA использует ядерные функции для выполнения извлечения признаков, что позволяет получить более точные результаты, чем обычная PCA.

Еще одним примером применения ядер в анализе данных является метод опорных векторов (SVM). SVM использует ядерные функции для проекции данных в пространство более высокой размерности, где они линейно разделимы. Это позволяет SVM эффективно работать с нелинейными данными.

Ядра также используются в кластерном анализе для определения сходства между объектами. Кластерный анализ позволяет группировать данные на основе их сходства, а использование ядерных функций может улучшить точность кластеризации.

Использование ядер в анализе данных открывает новые возможности в обработке и анализе больших объемов информации. Они позволяют извлекать более точные и содержательные признаки из данных, делают возможным работу с нелинейными данными и улучшают точность кластеризации.

ПрименениеПримеры ядерных функций

PCA	Гауссовское, полиномиальное, сигмоидальное
SVM	Линейное, радиально-базисное функционирование, полиномиальное
Кластерный анализ	Радиальное, Гауссовское, сигмоидальное