Что такое якобиан в математике

Якобиан – это матрица, состоящая из производных частных функций. В математике он играет важную роль в теории поля, анализе и дифференциальных уравнениях. Узнайте, как использовать якобиан для решения задач и понимания математических моделей.

Якобиан — это понятие из математического анализа, которое широко используется в различных областях науки и техники. Он является одним из основных инструментов для изучения и анализа функций многих переменных.

Определение якобиана связано с понятием производной. Якобиан функции нескольких переменных представляет собой матрицу, составленную из всех ее частных производных. Он позволяет оценить величину изменения функции при изменении независимых переменных.

Якобиан обладает рядом свойств, которые делают его полезным инструментом при решении различных задач. Например, якобиан может быть использован для нахождения обратной функции, для анализа локальных экстремумов и для вычисления определенных интегралов с заменой переменных.

Якобиан также находит применение в физике, экономике, геометрии и многих других научных дисциплинах. Он играет важную роль в решении задач, связанных с оптимизацией, определением равновесных состояний и моделированием сложных систем. Без использования якобиана невозможно представить современную математику и ее приложения.

В данной статье мы рассмотрим основные свойства якобиана и его применение в различных областях науки и техники. Мы также рассмотрим некоторые примеры вычисления якобиана и объясним, как использовать его для решения практических задач.

Что такое Якобиан?

Якобиан представляет собой матрицу первых производных между двумя наборами переменных. Если у нас есть два набора переменных, например, (x, y) и (u, v), Якобиан будет матрицей, состоящей из всех частных производных между парами переменных:

∂u/∂x	∂u/∂y
∂v/∂x	∂v/∂y

Якобиан может быть использован для преобразования координат в многомерном пространстве. Например, если у нас есть функция f(x, y), которая задает отображение из (x, y) в (u, v), мы можем использовать Якобиан, чтобы найти явные формулы для производных функции g(u, v), которая представляет собой обратное отображение.

Кроме того, Якобиан может быть использован для вычисления плотности вероятности при преобразовании случайных величин. Например, если у нас есть случайная величина x с плотностью вероятности p(x), и мы преобразуем ее через функцию f(x) в случайную величину y, мы можем использовать Якобиан, чтобы вычислить плотность вероятности p(y).

В общем случае, Якобиан позволяет нам изучать связи между различными переменными в многомерных системах и использовать эти связи для вычисления различных характеристик системы. Он играет важную роль во многих областях математики и физики, от теории вероятностей до дифференциальных уравнений и многомерного анализа.

Видео по теме:

Определение Якобиана

Формально, пусть у нас есть функция f, которая отображает n переменных в m переменных. Якобиан J этой функции определяется как:

J = ∂f1/∂x1 ∂f1/∂x2 … ∂f1/∂xn ∂f2/∂x1 ∂f2/∂x2 … ∂f2/∂xn … … … … ∂fm/∂x1 ∂fm/∂x2 … ∂fm/∂xn

Здесь ∂fi/∂xj обозначает частную производную fi по переменной xj. Якобиан является матрицей размерности m × n.

Якобиан широко применяется в различных областях математики и физики, включая дифференциальную геометрию, теорию вероятностей, теорию управления и многие другие. Он играет важную роль в понимании свойств и поведения функций и отображений.

Свойства Якобиана

1. Линейная зависимость: Если Якобиан равен нулю в некоторой точке, это означает, что векторы, заданные столбцами Якобиана, линейно зависимы. Такая информация может быть полезна при анализе систем уравнений и определении точек разрыва или особых точек.

2. Отображение: Якобиан дает информацию о том, как область входных переменных переходит в область выходных переменных. Он является мерой изменения масштаба и ориентации. Например, если Якобиан отображения равен единице, это означает, что область входных переменных сохраняется при отображении.

3. Обратное отображение: С использованием Якобиана можно вычислить Якобиан обратного отображения. Это позволяет определить, как изменятся входные переменные при заданном изменении выходных переменных. Такая информация может быть полезна при решении обратных задач и нахождении корней уравнений.

4. Многомерные переменные: Якобиан может быть обобщен на случай многомерных переменных. В этом случае он представляет собой матрицу частных производных и используется для описания связи между различными переменными в многомерных системах.

Свойства Якобиана делают его незаменимым инструментом в математике и находят применение в различных областях, таких как физика, экономика, статистика и машинное обучение.

Вопрос-ответ:

Что такое якобиан?

Якобиан — это определитель матрицы частных производных. Он используется для перехода от одной системы координат к другой и для вычисления многомерных интегралов. Якобиан является важным понятием в математическом анализе и математической физике.

Как вычислить якобиан?

Для вычисления якобиана необходимо найти частные производные всех переменных относительно других переменных и записать их в матрицу. Затем вычислить определитель этой матрицы. Если якобиан равен нулю, то это означает, что переменные связаны некоторым уравнением и система является вырожденной.

Какие свойства имеет якобиан?

Якобиан обладает несколькими важными свойствами. Во-первых, он является инвариантом при линейных преобразованиях координат. Во-вторых, если якобиан положителен, то это означает, что преобразование сохраняет ориентацию. Если якобиан отрицателен, то ориентация меняется. В-третьих, якобиан равен произведению якобианов обратного преобразования и самого преобразования.

В каких областях математики применяется якобиан?

Якобиан находит широкое применение в различных областях математики. Он используется в анализе функций многих переменных, в теории дифференциальных уравнений, в теории вероятностей, в геометрии и физике. Например, при решении задач о вычислении многомерных интегралов, при преобразовании системы координат, при определении глобальных свойств функций.

Значение Якобиана в математике

Значение Якобиана позволяет оценить, как функция меняет свои переменные при переходе от одной системы координат к другой. В частности, Якобиан используется для нахождения площади или объема, преобразуемого при замене переменных в интегралах.

Якобиан также имеет свойства, которые позволяют использовать его для решения различных задач. Например, Якобиан сохраняется при композиции функций и может быть использован для нахождения обратной функции. Он также играет важную роль в изучении локальных экстремумов и линейных преобразований.

В общем случае, Якобиан является полезным инструментом для анализа и решения задач, связанных с многомерными функциями и векторным анализом. Его значение простирается на различные области математики, такие как математическая физика, статистика, оптимизация и другие.

Применение Якобиана в физике

Одним из основных применений Якобиана является анализ движения тел в механике. С помощью Якобиана можно вычислить скорости и ускорения тела в зависимости от изменения параметров, таких как время или координаты. Это позволяет более точно описывать и предсказывать движение объектов в пространстве.

Якобиан также находит применение в термодинамике. Он позволяет анализировать связь между различными термодинамическими величинами, такими как давление, объем и энергия. С помощью Якобиана можно исследовать термодинамические процессы и оптимизировать работу систем, например, в случае газовых турбин или холодильных установок.

Еще одной областью, где применяется Якобиан, является электродинамика. Он позволяет анализировать связь между электрическими и магнитными полями, а также между токами и напряжениями в электрических цепях. С помощью Якобиана можно рассчитать электромагнитные поля и предсказать их взаимодействие с другими объектами.

Якобиан также используется в других областях физики, таких как оптика, квантовая механика и астрофизика. Он позволяет анализировать сложные системы и описывать их поведение с высокой точностью.

Таким образом, Якобиан является неотъемлемой частью физических исследований и позволяет углублять наше понимание природы и взаимодействия различных явлений.

Применение Якобиана в экономике

В экономике Якобиан применяется для изучения эластичности, которая является важным показателем для понимания реакции экономической системы на изменения входных параметров. Эластичность показывает, насколько процентное изменение одной переменной приведет к процентному изменению другой переменной.

Якобиан также используется для анализа макроэкономических моделей, таких как модель общего равновесия. Он позволяет исследовать взаимосвязи между различными секторами экономики и определить, как изменения в одном секторе могут повлиять на другие секторы.

Кроме того, Якобиан применяется для изучения финансовых рынков и определения рисков и доходности различных инвестиционных портфелей. Он помогает анализировать взаимосвязи между доходностью и риском, а также определить оптимальное соотношение между различными активами.

В целом, применение Якобиана в экономике позволяет более точно изучать взаимосвязи между различными переменными и предсказывать их влияние на экономическую систему. Это важный инструмент для принятия решений в области экономики и финансов, а также для разработки и анализа экономических моделей.

Применение Якобиана в биологии

Одним из основных применений Якобиана в биологии является исследование систем дифференциальных уравнений, которые описывают динамику биологических систем. Якобиан позволяет определить устойчивость равновесных состояний и предсказать поведение системы при изменении параметров.

Биологические модели, основанные на Якобиане, позволяют исследовать различные биологические процессы, такие как рост и развитие организмов, распространение инфекций, взаимодействие популяций и многое другое. Они помогают понять основные принципы и механизмы, лежащие в основе жизни на Земле.

Кроме того, Якобиан используется для анализа экспериментальных данных и оценки параметров в биологических моделях. Он позволяет оценить влияние каждого параметра на поведение системы и определить, какие параметры являются наиболее важными и требуют дальнейшего изучения.

Таким образом, применение Якобиана в биологии играет важную роль в понимании и моделировании сложных биологических процессов. Оно помогает ученым исследовать и объяснить разнообразие явлений, которые происходят в живых системах и являются основой для развития медицины, сельского хозяйства и биотехнологии.

Применение Якобиана в машинном обучении

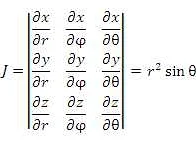
Одно из основных применений Якобиана в машинном обучении — это вариационный метод. Вариационные методы используются для нахождения параметров модели, оптимизирующих заданную целевую функцию. Якобиан позволяет оценить влияние изменения параметров модели на значение целевой функции, что позволяет найти оптимальные значения параметров.

Еще одно важное применение Якобиана — это обратное распространение ошибки, используемое в нейронных сетях. Обратное распространение ошибки позволяет эффективно обучать нейронные сети, настраивая их параметры таким образом, чтобы минимизировать ошибку на обучающем наборе данных. Якобиан используется для расчета градиента ошибки по параметрам сети, что позволяет обновлять параметры в направлении уменьшения ошибки.

Кроме того, Якобиан может быть использован для обнаружения аномалий в данных. Путем анализа Якобиана можно определить, какие параметры модели оказывают наибольшее влияние на результат и выявить необычные или выбросы в данных.

И наконец, Якобиан может быть использован при разработке алгоритмов градиентного спуска. Градиентный спуск — это метод оптимизации, используемый для нахождения локального минимума или максимума функции. Якобиан позволяет вычислить градиент функции, что позволяет определить направление наискорейшего убывания или возрастания функции и обновлять параметры модели в соответствии с этим направлением.

Таким образом, Якобиан играет важную роль в машинном обучении, позволяя решать разнообразные задачи, связанные с оптимизацией, обратным распространением ошибки и анализом данных.