Матрица в математике какой класс
Содержимое
- 1 Матрица в математике какой класс
- 1.1 Матрица в математике: разновидности и классификация
- 1.2 Определение и основные свойства
- 1.3 Квадратная матрица: определение и примеры
- 1.4 Прямоугольная матрица: особенности и применение
- 1.5 Симметрическая матрица: основные свойства и примеры
- 1.6 Диагональная матрица: специальный класс матриц
- 1.7 Треугольная матрица: определение и виды
- 1.8 Единичная матрица: роль и применение
- 1.9 Вопрос-ответ:
- 1.10 Нулевая матрица: свойства и примеры использования
- 1.11 Видео по теме:
Матрица в математике — это математический объект, представляющий собой прямоугольную таблицу чисел или символов. В зависимости от количества строк и столбцов, матрицы могут быть различных классов: квадратные, прямоугольные, нулевые, единичные и т.д. В данной статье рассмотрим различные классы матриц и их особенности.
Матрица — это одна из ключевых понятий в математике, которое широко используется в различных областях, включая линейную алгебру, теорию вероятностей, физику и компьютерные науки. Она представляет собой таблицу чисел, расположенных в определенном порядке. Каждое число в матрице называется элементом, а положение элемента определяется номером строки и столбца, в которых он находится.
Матрицы играют важную роль в линейной алгебре, где они используются для решения систем линейных уравнений, нахождения собственных значений и векторов, и других задач. В физике матрицы применяются для описания состояний квантовых систем, теории графов и многих других областей. В компьютерных науках матрицы используются для обработки изображений, анализа данных и машинного обучения.
Матрицы могут быть разных типов в зависимости от своих свойств и характеристик. Например, матрица может быть квадратной, если количество строк и столбцов совпадает. Она может быть симметричной, если она равна транспонированной матрице. Или матрица может быть диагональной, если все элементы вне главной диагонали равны нулю.
В общем, матрицы являются мощным и универсальным инструментом в математике, который позволяет удобно и эффективно работать с большими объемами данных и решать сложные задачи. Изучение матриц и их свойств является неотъемлемой частью математического образования и имеет широкие приложения в реальном мире.
Матрица в математике: разновидности и классификация
Матрицы могут иметь различные разновидности и классифицируются в зависимости от их размерности, содержимого и применения в математических задачах.
Основные разновидности матриц:
- Прямоугольная матрица — матрица, у которой количество строк и столбцов может быть различным.
- Квадратная матрица — матрица, у которой количество строк и столбцов одинаковое.
- Диагональная матрица — матрица, у которой все элементы, кроме элементов на главной диагонали, равны нулю.
- Треугольная матрица — матрица, у которой все элементы, расположенные выше (ниже) главной диагонали, равны нулю.
Классификация матриц также осуществляется по их содержимому и назначению:
- Нулевая матрица — матрица, все элементы которой равны нулю.
- Единичная матрица — квадратная матрица, у которой все элементы на главной диагонали равны единице, а все остальные элементы равны нулю.
- Симметричная матрица — квадратная матрица, у которой элементы симметричны относительно главной диагонали.
- Операторная матрица — матрица, которая описывает линейное отображение между двумя векторными пространствами.
Матрицы играют важную роль в различных областях математики, физики, экономики, компьютерных наук и других научных дисциплинах. Изучение и анализ матриц позволяет решать широкий спектр задач, таких как решение систем линейных уравнений, поиск собственных значений и векторов, аппроксимация данных и многое другое.
Определение и основные свойства

Основные свойства матрицы включают:
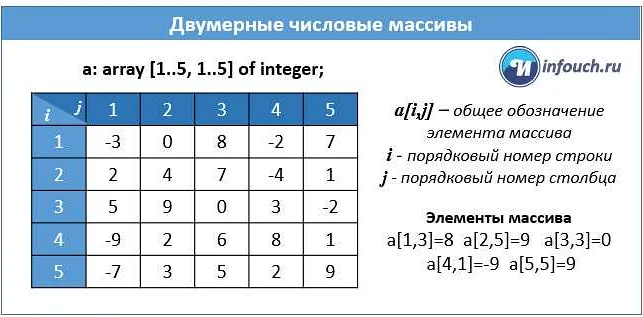
- Размерность: матрицы характеризуются количеством строк и столбцов. Например, матрица размерности 2×3 имеет две строки и три столбца.
- Элементы: каждый элемент матрицы может быть числом, переменной или выражением.
- Равенство: две матрицы равны, если они имеют одинаковую размерность и все их элементы равны.
- Сложение: матрицы одинаковой размерности могут быть сложены путем сложения соответствующих элементов.
- Умножение на число: каждый элемент матрицы может быть умножен на число.
- Умножение: умножение матрицы на другую матрицу определено только в случае, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Матрицы широко используются в математике, физике, экономике и компьютерных науках. Они играют важную роль в решении систем линейных уравнений, представлении преобразований и обработке данных.
Квадратная матрица: определение и примеры
Квадратные матрицы важны во многих областях математики и физики. Они находят применение в алгебре, теории вероятности, линейном программировании и других дисциплинах.
Примеры квадратных матриц:
- Матрица 2 × 2:| a b |
| c d | - Матрица 3 × 3:| a b c |
| d e f |
| g h i | - Матрица 4 × 4:| a b c d |
| e f g h |
| i j k l |
| m n o p |
Квадратная матрица может быть как нулевой (все элементы равны нулю), так и единичной (диагональные элементы равны единице, а остальные элементы равны нулю).
Прямоугольная матрица: особенности и применение
Особенностью прямоугольной матрицы является то, что она позволяет представить различные типы данных в удобной форме. Например, матрицу можно использовать для хранения данных о студентах в таблице, где каждая строка представляет собой отдельного студента, а столбцы содержат информацию о его имени, возрасте, оценках и т.д.
Прямоугольные матрицы широко применяются в различных областях, включая математику, физику, экономику и информатику. В математике они используются для решения систем линейных уравнений, анализа данных и численных методов. В физике прямоугольные матрицы помогают описывать физические процессы и моделировать различные системы. В экономике они применяются для анализа рынка, прогнозирования и оптимизации бизнес-процессов. В информатике прямоугольные матрицы используются для работы с графами, обработки изображений и многих других задач.
Преимуществом прямоугольных матриц является их гибкость и универсальность. Они позволяют представить и обрабатывать большие объемы данных в удобной и компактной форме. Кроме того, прямоугольные матрицы позволяют использовать различные операции, такие как сложение, умножение, транспонирование и обратная матрица, что делает их полезными инструментами при решении различных задач.
Симметрическая матрица: основные свойства и примеры
Основные свойства симметрической матрицы:
- Главная диагональ матрицы содержит значения, остальные элементы симметричны относительно нее.
- Если элемент (i, j) симметрической матрицы равен a, то элемент (j, i) также равен a.
- Сумма и разность двух симметрических матриц также являются симметрическими матрицами.
- Умножение симметрической матрицы на скаляр также дает симметрическую матрицу.
- Транспонирование симметрической матрицы не меняет ее, так как она уже симметрична.
Примеры симметрических матриц:
- Матрица единичного порядка.
- Матрица диагонального вида, где все элементы на главной диагонали равны друг другу.
- Матрица симметричного вида, где элементы на главной диагонали равны, а значения остальных элементов симметричны относительно нее.
Симметрические матрицы играют важную роль в различных областях математики и естественных науках, например, в линейной алгебре, теории графов, физике и теории вероятностей. Их свойства и особенности делают их полезными инструментами для изучения и решения различных математических задач.
Диагональная матрица: специальный класс матриц
Диагональные матрицы обозначаются символом D и имеют следующий вид:
- Если все элементы главной диагонали равны одному числу d, то матрица называется скалярной диагональной матрицей и записывается как D = [d].
- Если элементы главной диагонали различны, то матрица называется недиагональной диагональной матрицей и записывается как D = [d1, d2, …, dn], где di — элементы главной диагонали.
Особенности диагональных матриц:
- Умножение диагональной матрицы на скаляр равносильно умножению каждого элемента главной диагонали на этот скаляр.
- Умножение двух диагональных матриц равносильно умножению элементов их главных диагоналей.
- Обратная матрица для диагональной матрицы существует только в том случае, если все элементы главной диагонали не равны нулю.
Диагональные матрицы находят широкое применение в различных областях математики и физики, особенно в линейной алгебре и теории вероятностей.
Треугольная матрица: определение и виды
Треугольные матрицы могут быть двух видов: верхнетреугольные и нижнетреугольные.
Верхнетреугольная матрица – это треугольная матрица, у которой все элементы ниже главной диагонали равны нулю.
Нижнетреугольная матрица – это треугольная матрица, у которой все элементы выше главной диагонали равны нулю.
Треугольные матрицы находят широкое применение в алгебре и линейной алгебре. Они позволяют упростить решение систем линейных уравнений и решение других математических задач.
Единичная матрица: роль и применение

1 0 0
0 1 0
0 0 1
Единичная матрица играет важную роль в линейной алгебре и математическом анализе. Она является нейтральным элементом относительно умножения матриц. То есть, если матрицу A умножить на единичную матрицу E, то результатом будет сама матрица A:
A * E = E * A = A
Это свойство позволяет использовать единичную матрицу в решении линейных систем уравнений, нахождении обратной матрицы, вычислении определителя и других операциях с матрицами.
Единичная матрица также применяется в компьютерной графике, машинном обучении, криптографии и других областях. Она может быть использована для преобразования координатных систем, поворота и масштабирования объектов, а также для кодирования и дешифрования информации.
Вопрос-ответ:
Какой математический класс относится матрица?
Матрица относится к классу объектов линейной алгебры.
В чем заключается основная идея матрицы в математике?
Основная идея матрицы в математике заключается в представлении и обработке линейных отображений и систем линейных уравнений.
Какие операции можно выполнять с матрицами?
С матрицами можно выполнять операции сложения, вычитания, умножения, транспонирования и нахождения определителя.
Каковы применения матриц в реальной жизни?
Матрицы широко применяются в различных областях, включая физику, экономику, компьютерную графику, машинное обучение и т.д. Например, они используются для решения систем линейных уравнений, моделирования физических процессов, анализа данных и прогнозирования.
Какая связь между матрицами и векторами?
Матрицы и векторы тесно связаны в линейной алгебре. Векторы могут быть представлены как специальные виды матриц (вектор-столбцы или вектор-строки), а умножение матрицы на вектор является одной из основных операций.
Нулевая матрица: свойства и примеры использования

Свойства нулевой матрицы:
- Все элементы нулевой матрицы равны нулю.
- Сумма нулевой матрицы с любой другой матрицей A равна самой матрице A: O + A = A.
- Произведение нулевой матрицы на любую другую матрицу B равно нулевой матрице: O × B = O.
- Умножение нулевой матрицы на число c также дает нулевую матрицу: c × O = O.
Примеры использования нулевой матрицы:
- В линейной алгебре нулевая матрица используется как базовый элемент для определения других матричных операций и свойств.
- В компьютерной графике нулевая матрица может использоваться для задания начальных координат или очистки изображения.
- В программировании нулевая матрица может служить исходным состоянием для матричных операций или хранения информации о состоянии системы.


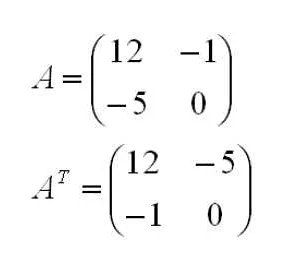

Матрица в математике — фундаментальное понятие, используемое в различных разделах науки. Она является одним из важнейших инструментов для решения линейных систем уравнений и описания линейных преобразований. Матрицы находят применение в физике, экономике, компьютерной графике и других областях. Основная идея матрицы заключается в представлении данных в виде прямоугольной таблицы, состоящей из элементов, называемых элементами матрицы. Каждый элемент имеет свою позицию в таблице, определяемую номером строки и столбца. Такая структура данных позволяет эффективно хранить и обрабатывать большие объемы информации. В зависимости от свойств и характеристик матрицы, она может быть классифицирована. Например, матрицы могут быть квадратными (количество строк равно количеству столбцов) или прямоугольными. Они также могут быть нулевыми, единичными или диагональными, в зависимости от значений элементов. Матрицы играют важную роль в линейной алгебре, где они являются основой для решения систем линейных уравнений. Они также используются для описания линейных преобразований, таких как повороты, масштабирование и сдвиги. Благодаря своим свойствам и универсальности, матрицы стали неотъемлемой частью многих научных и практических дисциплин, помогая упростить и эффективно решить сложные задачи.
Эта статья очень интересна и полезна для всех, кто хочет углубить свои знания в математике. Матрицы — это мощный инструмент, который широко используется в различных областях, начиная от линейной алгебры и заканчивая программированием и машинным обучением. Я всегда интересовался математикой, и матрицы всегда были одной из моих любимых тем. Чтение этой статьи помогло мне лучше понять, как матрицы классифицируются и как их можно использовать для решения различных задач. В статье подробно рассматривается классификация матриц по их размерности и свойствам, таким как квадратность, симметричность и диагональность. Также описывается, как матрицы связаны с линейными операторами и системами линейных уравнений. Особое внимание уделено основным операциям над матрицами, таким как сложение, умножение и нахождение обратной матрицы. Это позволяет решать системы уравнений и находить собственные значения и собственные векторы. Мне понравилась четкая и логичная структура статьи, а также примеры и задачи, которые помогли закрепить материал. Я узнал много нового о матрицах и теперь смогу применять свои знания на практике. В целом, я рекомендую эту статью всем, кто хочет углубить свои знания в математике и линейной алгебре. Она поможет вам лучше понять матрицы и их классификацию, а также научит вас применять их для решения различных задач.
Статья очень понятно и доступно объясняет, какую роль матрицы играет в математике. Матрица – это структура данных, которая позволяет удобно представлять и решать системы линейных уравнений. Я согласен со всеми примерами, которые автор приводит, чтобы продемонстрировать применение матриц в различных областях науки и техники. Важно отметить, что матрицы являются основой для многих других математических понятий и операций, таких как определители, транспонирование и умножение. Эта статья вызвала у меня интерес и заставила задуматься о том, как можно применить матрицы в своей повседневной жизни. Обязательно буду искать дополнительную информацию на эту тему.
Матрица в математике — это мощный инструмент, который применяется во многих областях. Она является одним из фундаментальных понятий линейной алгебры и широко применяется в физике, экономике, компьютерной графике и других науках. Матрица представляет собой таблицу, состоящую из числовых элементов, расположенных в строках и столбцах. Одним из главных свойств матрицы является возможность производить операции с ее элементами. С помощью матриц можно решать системы линейных уравнений, находить обратные матрицы, находить собственные значения и векторы, а также многое другое. Благодаря этим свойствам матрица является мощным инструментом для моделирования реальных процессов и анализа данных. Класс матриц зависит от их размерности и элементов. Существуют такие классы матриц, как квадратные, прямоугольные, диагональные, верхнетреугольные, нижнетреугольные и другие. Каждый класс имеет свои особенности и применяется в разных областях. Матрица — это не просто набор чисел, это мощный инструмент, который позволяет нам решать сложные математические задачи и анализировать данные. Изучение матриц поможет нам развить логическое мышление и улучшить наши навыки в математике.