Что такое координат в математике

Координаты в математике — это числовые значения, которые используются для определения положения точки в пространстве или на плоскости. Они состоят из двух или трех чисел, которые представляют собой расстояние до определенных осей. Понимание координат является важным фундаментом для работы с геометрией, алгеброй и другими областями математики.

Координаты – это числовые значения, которые используются для определения положения точек на плоскости или в пространстве. Они представляют собой измерения относительно определенных осей.

В математике координаты широко применяются для описания и изучения геометрических фигур, решения уравнений и построения графиков функций. Они позволяют наглядно представить различные математические объекты и процессы.

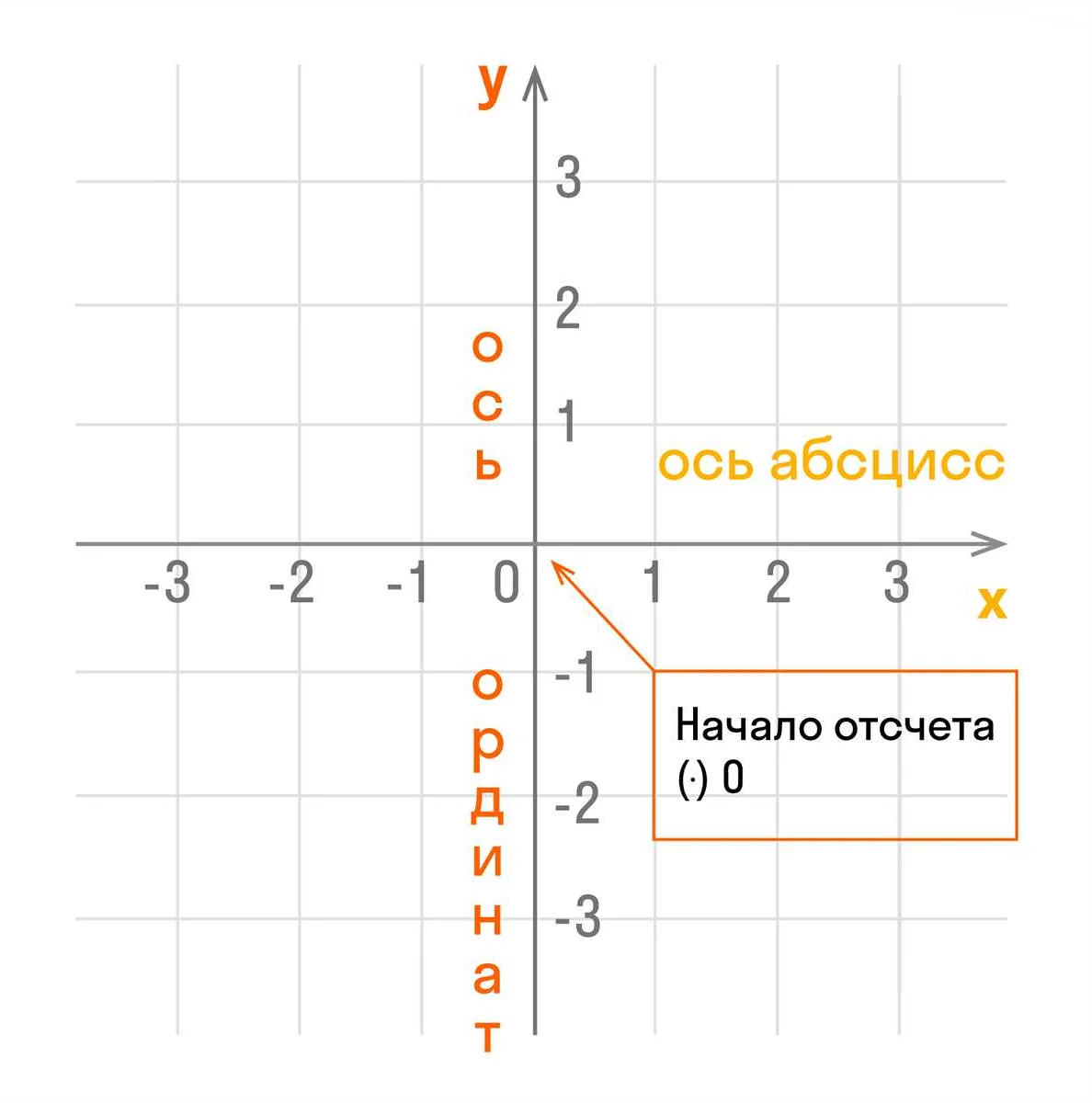
Особенностью координат является то, что они могут быть представлены в различных системах. Наиболее распространенной системой координат является декартова система координат, которая основана на двух взаимно перпендикулярных осях – горизонтальной (ось абсцисс) и вертикальной (ось ординат).

В декартовой системе координат каждая точка на плоскости имеет свои уникальные координаты, которые обозначаются парой чисел (x, y), где x – это значение по горизонтальной оси, а y – по вертикальной.

Координаты также используются в других системах, таких как полярная и сферическая системы координат, которые вводятся для более удобного описания объектов в пространстве.

Определение и основные понятия

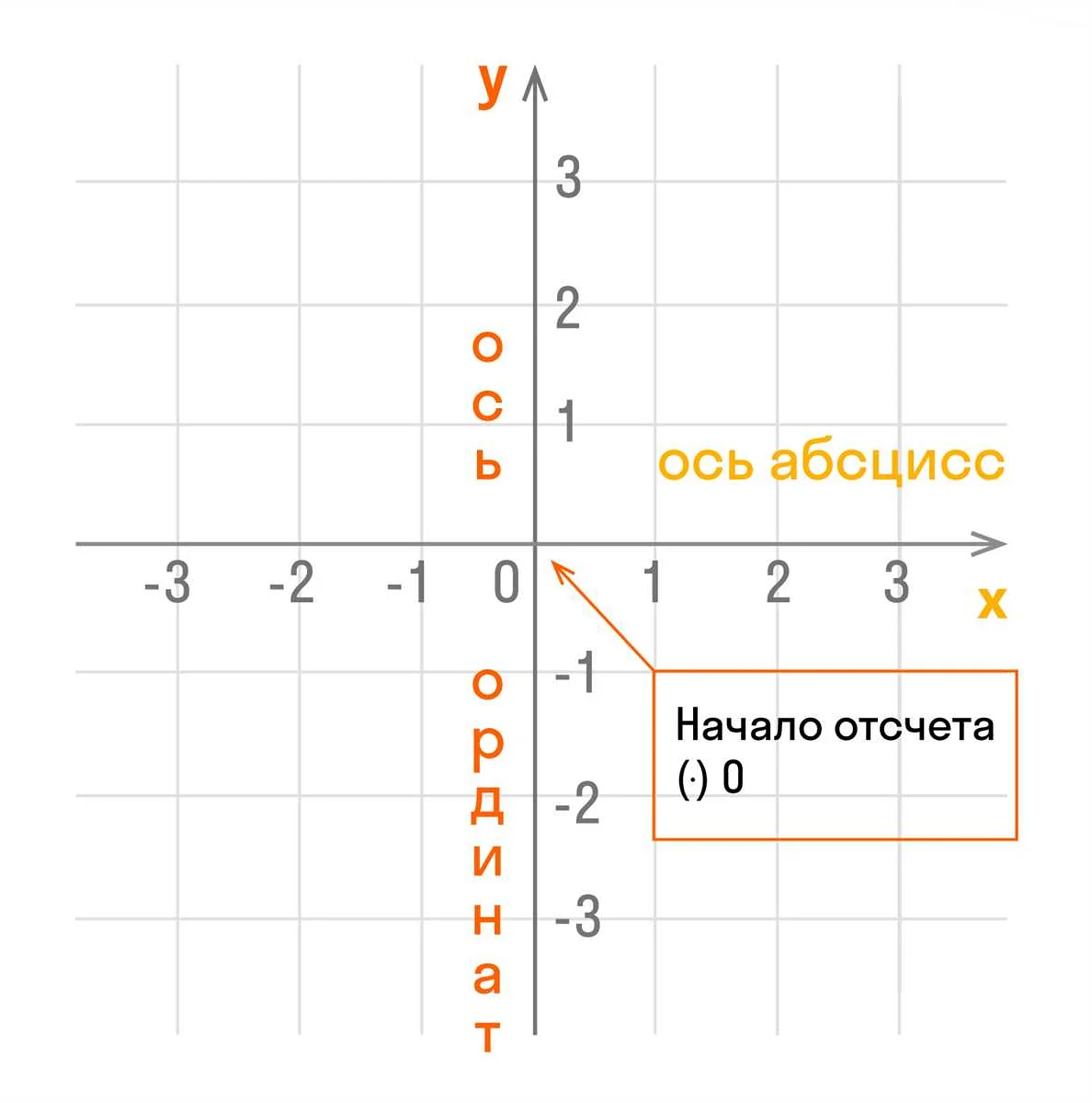
В двумерной координатной системе каждая точка задается парой чисел (x, y), где x – это горизонтальная координата, а y – вертикальная координата. Начало координат обозначается точкой (0, 0) и называется началом системы.

В трехмерной координатной системе каждая точка задается тройкой чисел (x, y, z), где x, y и z – это координаты точки по осям x, y и z соответственно. Начало координат обозначается точкой (0, 0, 0) и также называется началом системы.

Координаты широты и долготы используются для определения местоположения на поверхности Земли. Широта измеряется отдельно для каждой точки и указывает на расстояние от данной точки до экватора. Долгота же измеряется отдельно для каждой точки и указывает на расстояние от данной точки до меридиана Гринвича.

Важно отметить, что различные системы координат могут иметь разные единицы измерения и масштабы. Также существуют различные способы задания и использования координат, например, в геометрии, физике, географии и других науках.

Применение координат в геометрии

Одним из основных способов использования координат в геометрии является задание точек на плоскости. Каждой точке на плоскости можно сопоставить уникальную пару координат (x, y), где x — это горизонтальная координата (абсцисса), а y — вертикальная координата (ордината). Это позволяет однозначно определить положение точки и использовать ее в дальнейших расчетах и построениях.

Координаты также применяются для описания и изучения геометрических фигур, таких как прямые, окружности, треугольники и др. Например, уравнение прямой в декартовой системе координат задается уравнением y = kx + b, где k — это угловой коэффициент, а b — коэффициент смещения. Это позволяет анализировать свойства прямых, находить их точки пересечения и т.д.

Также координаты используются для определения расстояний между точками, углов между прямыми и плоскостями, площадей и объемов фигур и других задач в геометрии. Они позволяют более точно и удобно работать с геометрическими объектами, а также анализировать их свойства и взаимосвязи.

Использование координат в геометрии является неотъемлемой частью этой науки и позволяет более глубоко изучать и понимать геометрические объекты и их свойства.

Применение координат в физике

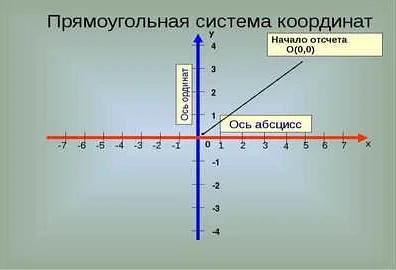
В физике координаты используются для описания положения тела или точки в трехмерном пространстве. Координаты вводятся в системе отсчета, которая может быть выбрана произвольно, но должна быть однозначно определена. Обычно в физике используется прямоугольная система координат, состоящая из трех перпендикулярных осей X, Y и Z.

ОсьПоложительное направлениеОтрицательное направление

X	Вправо	Влево
Y	Вверх	Вниз
Z	К наблюдателю	От наблюдателя

Координаты используются для описания перемещения объектов, скорости, ускорения и других физических величин. Например, при изучении движения тела в пространстве, координаты позволяют определить его положение в каждый момент времени и вычислить его скорость и ускорение.

Также координаты применяются для описания положения и движения частиц внутри атомов и молекул. В квантовой физике координаты используются для описания энергетических уровней, волновых функций и вероятности нахождения частицы в определенной области пространства.

Применение координат в физике позволяет установить точные зависимости между различными физическими величинами, а также предсказывать и объяснять различные явления и процессы в природе. Они являются важным инструментом для разработки физических моделей, проведения экспериментов и прогнозирования результатов.

Применение координат в экономике

Координаты играют важную роль в экономике, так как позволяют представить и анализировать различные экономические явления и процессы. С помощью координат можно отобразить графики и диаграммы, которые позволяют визуально представить данные и сделать выводы.

Одно из основных применений координат в экономике – построение спроса и предложения. С помощью координат можно построить график спроса и предложения на товары или услуги, что позволяет определить равновесную цену и объем продаж. Также координаты позволяют анализировать изменения спроса и предложения в различных условиях и прогнозировать их влияние на рыночные процессы.

Координаты также используются для анализа рыночной концентрации. С помощью координат можно построить график, на котором отображается доля рынка, занимаемая каждым участником. Это позволяет определить степень конкуренции на рынке и оценить влияние доминирующих фирм на цены и объемы производства.

Координаты широко применяются также для анализа экономического роста и развития. С помощью координат можно отобразить динамику ВВП, индексов цен, объемов производства и других экономических показателей. Это позволяет анализировать тенденции и цикличность развития экономики, а также прогнозировать ее будущее состояние.

Таким образом, координаты являются важным инструментом для анализа и визуализации экономических данных. Они позволяют лучше понять и представить различные экономические явления и процессы, что помогает принимать решения и строить прогнозы в экономике.

Видео по теме:

Вопрос-ответ:

Какие области науки и техники используют координаты?

Координаты широко применяются в различных областях науки и техники. Они являются основой для работы в геометрии, физике, астрономии, компьютерной графике, навигации и других дисциплинах.

Что такое система координат?

Система координат — это математический инструмент, который используется для определения положения точки в пространстве или на плоскости. Она состоит из осей и начала координат, и позволяет задавать координаты точки с помощью числовых значений.

Какие виды систем координат существуют?

Существует несколько видов систем координат, в зависимости от их применения и особенностей. Наиболее распространены декартова система координат, полярная система координат и сферическая система координат.

Зачем нужны координаты в математике?

Координаты играют важную роль в математике, так как позволяют определить положение объектов в пространстве и на плоскости. Они используются для решения геометрических задач, построения графиков функций, анализа движения и многое другое.

Применение координат в компьютерной графике

Координаты играют важную роль в компьютерной графике, где они используются для определения позиции и размеров объектов на экране. Координатная система, основанная на прямоугольных координатах, позволяет точно задавать положение пикселей, линий, фигур и текста.

В компьютерной графике используется двумерная координатная система, где каждая точка на экране имеет свои координаты — горизонтальные (x) и вертикальные (y). Начало координат обычно располагается в левом верхнем углу экрана, а оси x и y направлены вправо и вниз соответственно.

Координаты в компьютерной графике позволяют создавать и отображать различные графические объекты, такие как прямоугольники, круги, линии и многое другое. При рисовании графики на экране, программист указывает координаты начальной и конечной точек, а компьютер автоматически соединяет их линией или создает другой графический объект.

Координаты также используются в компьютерных играх для определения положения игровых персонажей, препятствий и других элементов на экране. Они позволяют управлять движением объектов и их взаимодействием с окружающей средой.

Кроме того, координаты применяются в компьютерной графике для создания трехмерных изображений и анимации. Трехмерные координаты (x, y, z) позволяют задавать положение объектов в пространстве и определять их относительное расположение.

В заключение, применение координат в компьютерной графике является основополагающим принципом, который позволяет точно задавать положение и форму графических объектов на экране. Без использования координат систематизация и создание сложных изображений стало бы практически невозможным.

Особенности использования координат

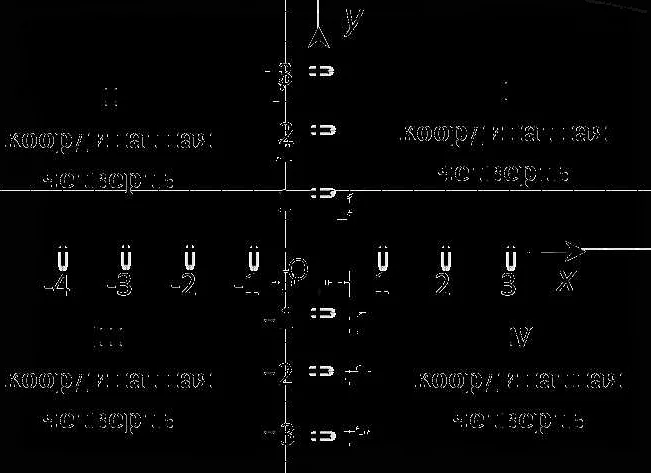
Одной из особенностей использования координат является выбор системы координат. Существует несколько типов систем координат, таких как декартова, полярная, сферическая и цилиндрическая системы координат. Каждая система имеет свои особенности и предназначена для работы с определенными типами задач.

Другой важной особенностью координат является их применение в различных областях, включая физику, геометрию, картографию, компьютерную графику и другие. В физике координаты используются для описания движения тела или расположения точки в пространстве. В геометрии координаты позволяют определить расстояние между точками или угол между векторами. В картографии координаты используются для построения карт и определения местоположения объектов на Земле. В компьютерной графике координаты используются для отображения объектов на экране и управления их положением и размером.

Координаты также имеют свои особенности в плоскости и пространстве. В плоскости координаты представляются парой чисел (x, y), где x — это координата по горизонтальной оси, а y — по вертикальной. В пространстве координаты представляются тройкой чисел (x, y, z), где z — это координата по оси глубины.

Использование координат позволяет точно определить положение объекта или точки в пространстве, что делает их незаменимым инструментом в научных и прикладных областях. Понимание особенностей использования координат помогает решать различные задачи и улучшать качество работы в соответствующих областях.