Математика как найти объем

Узнайте, как вычислить объем различных геометрических фигур, включая прямоугольники, кубы, цилиндры и сферы. Подробные инструкции и примеры расчетов объема для каждой фигуры.

Математика является одной из основных наук, которая изучает числа, структуры, пространство и изменения. В математике существует много различных понятий, одним из которых является объем. Объем — это мера пространства, занимаемого телом или фигурой. Нахождение объема является важной задачей во многих областях, таких как инженерия, физика и архитектура.

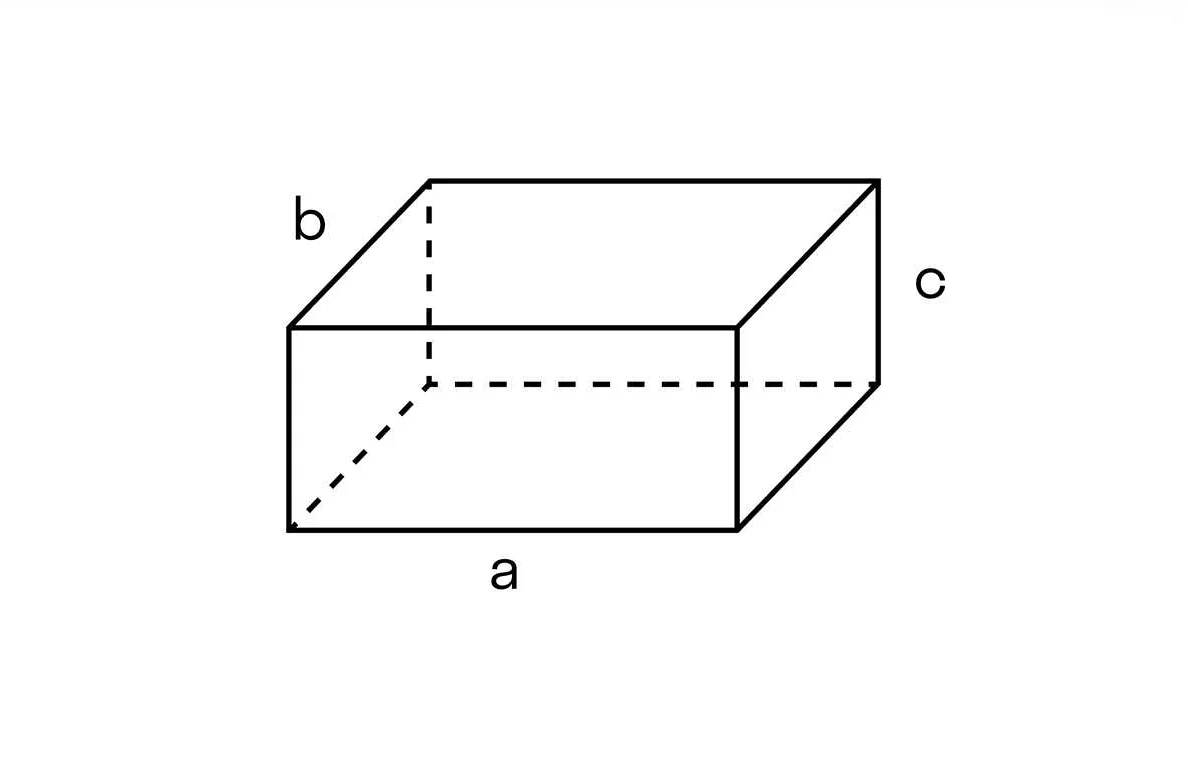
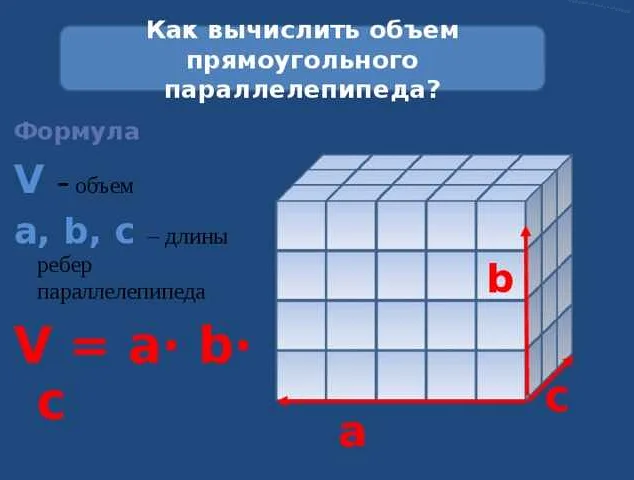
Основным принципом нахождения объема является понимание формы и размеров объекта. В зависимости от формы объекта, существуют различные формулы для вычисления объема. Например, для прямоугольного параллелепипеда объем вычисляется по формуле V = a * b * c, где a, b и c — это длины сторон параллелепипеда.

Примечание: Для нахождения объема объекта необходимо знать его форму и размеры. Если форма объекта сложная, то обычно применяются более сложные математические методы, такие как интегралы и дифференциальные уравнения.

Кроме того, для нахождения объема необходимо знать единицы измерения. Объем измеряется в кубических единицах, таких как кубический метр (м³) или кубический дециметр (дм³). Поэтому при вычислении объема необходимо учесть соответствующие единицы измерения и правильно перевести их, если это требуется.

Определение понятия «объем»

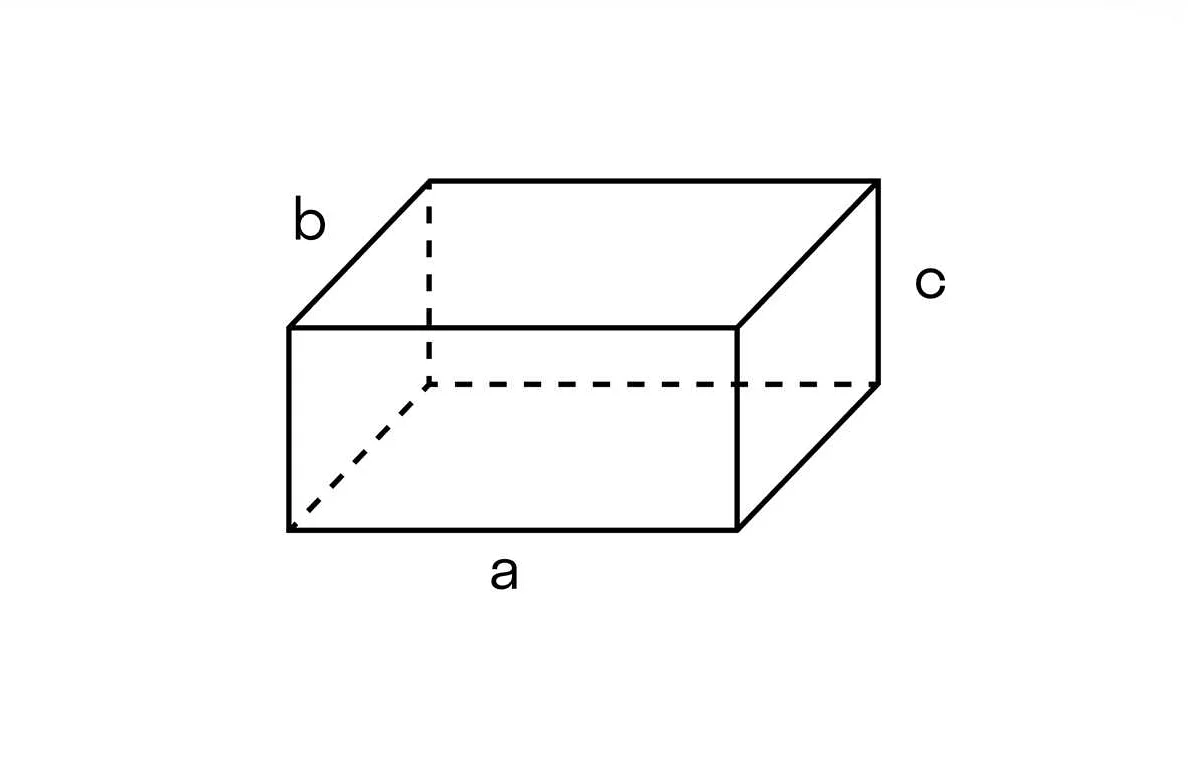
Объем обычно выражается в кубических единицах измерения, таких как кубический метр (м³), кубический сантиметр (см³) или кубический дециметр (дм³). Однако, в зависимости от контекста, объем может быть выражен и в других единицах измерения, например, литрах (л) или галлонах (gal).

Для определения объема необходимо знать геометрические параметры объекта, такие как длина, ширина и высота, или радиус и высоту в случае цилиндра. Существует множество формул для вычисления объема различных геометрических фигур, например, параллелепипеда, сферы, конуса и т.д.

Знание понятия «объем» является важным для решения задач в различных областях, таких как архитектура, строительство, геометрия, физика и химия. Понимание основных принципов математики, связанных с определением объема, позволяет лучше понимать и анализировать окружающий мир и решать практические задачи.

Видео по теме:

Зачем нужно знать объем

• Рассчитывать объемы различных фигур и тел, таких как параллелепипеды, цилиндры, конусы, сферы и другие. Это особенно полезно в строительстве и архитектуре, где необходимо определить объемы помещений, емкостей, естественных и искусственных объектов.
• Измерять и сравнивать объемы жидкостей и газов. Знание объема позволяет рассчитывать какую-либо величину, например, количество жидкости, на основе ее объема. Это важно в химии, физике, медицине и других науках.
• Оценивать необходимое количество материалов для производства или изготовления изделий. Знание объема позволяет рассчитать, сколько материала потребуется для изготовления определенного изделия или строительства объекта. Это важно в промышленности, производстве и ремонте.
• Определять плотность и массу тела, используя объем. Знание объема позволяет рассчитать плотность тела или вещества, а также массу этого тела или вещества, если известна плотность. Это важно в физике, химии, науке о материалах и других областях.

В целом, знание объема является неотъемлемой частью математической грамотности и может быть полезно в различных аспектах жизни, от повседневных задач до специализированных профессиональных областей.

Основные принципы математики

Один из основных принципов математики – это принцип уникальности. Он гласит, что для любого объекта существует только одна математическая истина. Это означает, что любые математические утверждения должны быть доказаны и проверены с использованием строгих логических рассуждений.

Еще один важный принцип – это принцип независимости. Он говорит о том, что математические объекты и операции не зависят от контекста или физических условий. Например, сложение двух чисел всегда будет давать один и тот же результат, независимо от того, где или когда это происходит.

Также в математике существует принцип композиции, который утверждает, что сложные математические объекты и операции могут быть разбиты на более простые части. Это позволяет упростить сложные задачи и решать их пошагово.

Более того, математика руководствуется принципом эквивалентности, который гласит, что два объекта или операции могут быть считаться равными, если они имеют одинаковые свойства или выполняют одну и ту же функцию. Это позволяет сравнивать и классифицировать математические объекты и операции.

Необходимо отметить, что эти принципы математики обеспечивают надежное и строгое основание для развития математических концепций и их применения в различных областях науки, техники и повседневной жизни.

Вопрос-ответ:

Как найти объем прямоугольного параллелепипеда?

Чтобы найти объем прямоугольного параллелепипеда, нужно умножить длину на ширину на высоту этого параллелепипеда.

Как найти объем цилиндра?

Для нахождения объема цилиндра нужно умножить площадь основания на высоту этого цилиндра.

Как найти объем шара?

Чтобы найти объем шара, нужно воспользоваться формулой: V = (4/3)πr^3, где r — радиус шара.

Как найти объем пирамиды?

Для нахождения объема пирамиды нужно умножить площадь основания на высоту этой пирамиды и разделить полученное произведение на 3.

Принцип добавления

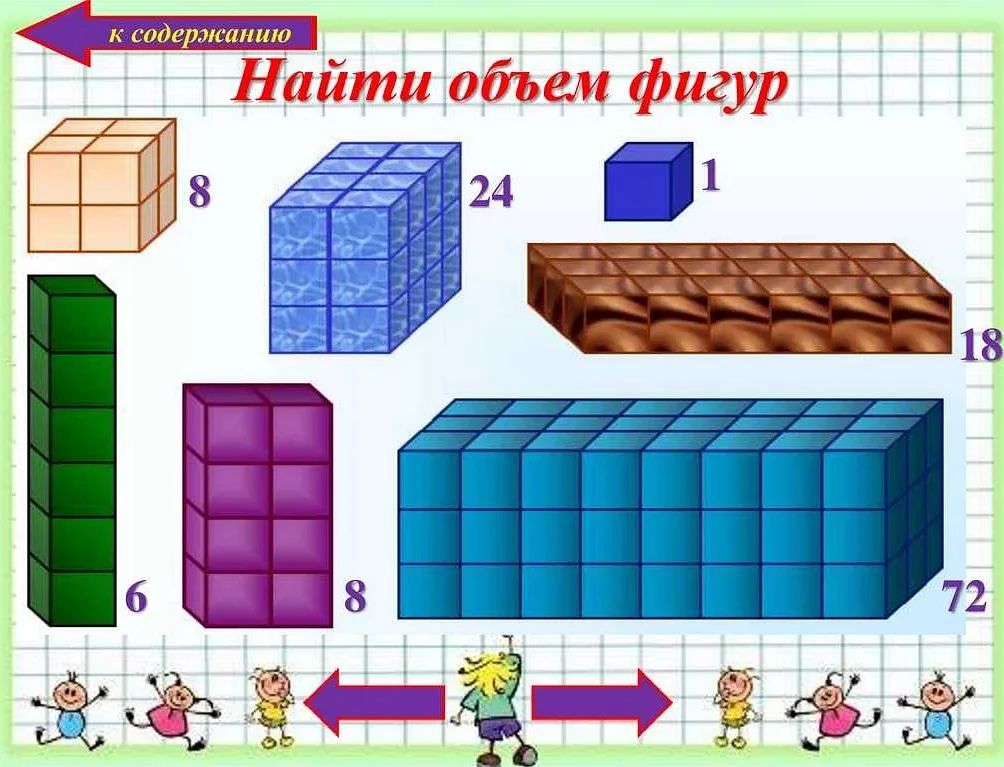
Согласно принципу добавления, объем фигуры или тела можно получить путем сложения объемов его составных частей. То есть, если фигура состоит из нескольких частей, то объем фигуры равен сумме объемов каждой из этих частей.

Применение принципа добавления позволяет упростить расчет объема сложных фигур, а также найти объем фигуры, состоящей из известных элементов. Например, для нахождения объема параллелепипеда можно разбить его на прямоугольные блоки и сложить объемы каждого из этих блоков.

Принцип добавления является основой для других математических принципов, таких как принцип включения-исключения и принцип умножения. Он широко используется в геометрии, физике, архитектуре и других областях, где требуется нахождение объема фигур и тел.

Принцип вычитания

Для применения принципа вычитания необходимо знать объемы исходных фигур. Если мы знаем объем первой фигуры и объем второй фигуры, то просто вычитаем объем второй фигуры из объема первой фигуры и получаем объем полученной фигуры.

Принцип вычитания широко применяется в геометрии и физике. Например, для нахождения объема полого тела можно вычесть объем внутренней полости из объема внешней оболочки.

Важно отметить, что принцип вычитания применим только в случае, когда объем вычитаемой фигуры полностью содержится внутри объема исходной фигуры. В противном случае, результат будет некорректным.

Принцип вычитания является одним из базовых принципов математики, который позволяет находить объемы сложных фигур путем вычитания объемов простых фигур.

Принцип умножения

Принцип умножения утверждает, что если у нас есть два независимых события, и первое событие может произойти m способами, а второе событие может произойти n способами, то общее количество возможных исходов будет равно произведению m на n.

Этот принцип широко применяется в математике и других областях, где необходимо определить количество возможных комбинаций и вариантов.

Например, если у нас есть 2 различных цвета шаров и 3 различных цвета корзин, то количество возможных комбинаций будет равно 2 умножить на 3, то есть 6.

Принцип умножения является важной основой для решения задач, связанных с определением объема, и позволяет более точно и эффективно работать с математическими моделями.

Принцип деления

Этот принцип основан на идее разбиения сложной фигуры на более простые подфигуры, объемы которых можно найти отдельно.

Для применения принципа деления часто используется таблица, в которой перечисляются все составляющие фигуры и их объемы. Затем эти объемы суммируются, чтобы получить общий объем фигуры.

Принцип деления может быть применен для нахождения объема таких фигур, как прямоугольные параллелепипеды, цилиндры, конусы и т.д.

ФигураОбъем

Прямоугольный параллелепипед	V = a * b * c
Цилиндр	V = π * r^2 * h
Конус	V = 1/3 * π * r^2 * h

Применение принципа деления позволяет более эффективно находить объем сложных фигур, разбивая их на более простые составляющие части.

Как найти объем

Для каждой фигуры существуют специальные формулы для расчета объема. Например, для параллелепипеда объем вычисляется по формуле:

объем = длина * ширина * высота

Для сферы формула будет выглядеть следующим образом:

объем = 4/3 * π * радиус^3

Для конуса формула будет:

объем = 1/3 * π * радиус^2 * высота

Чтобы найти объем, необходимо знать соответствующие параметры фигуры. Обычно они представляют собой длину, ширину, высоту или радиус фигуры. Подставив значения параметров в соответствующую формулу, можно легко вычислить объем.

Кроме того, существуют также специальные приближенные методы для расчета объема сложных фигур, таких как интегральные методы, метод Монте-Карло и др. Они используются в математике, физике и других областях науки для более точного определения объема.

Зная основные принципы математики и формулы для расчета объема, можно легко решать задачи, связанные с определением объема различных фигур. Это применимо не только в школьных упражнениях, но и в реальной жизни, например, при расчете объема жидкостей, объема объектов или расчете пространства.

Объем геометрических фигур

Объем различных геометрических фигур рассчитывается по-разному и зависит от их формы и размеров. Некоторые из наиболее распространенных геометрических фигур, для которых можно найти объем, включают:

• Параллелепипеды
• Пирамиды
• Цилиндры
• Шары
• Конусы

Для каждой из этих фигур существуют специальные формулы с учетом их характеристик, которые позволяют вычислить их объем. Например, объем параллелепипеда можно найти, умножив длину, ширину и высоту, а объем шара — умножив четверть числа Пи на радиус в кубе.

Понимание принципов вычисления объема геометрических фигур является важной составляющей математической грамотности и может быть полезно в решении практических задач в различных областях, таких как архитектура, инженерия и физика.

Объем тела вращения

Для вычисления объема тела вращения с помощью математических методов используется интеграл. Для этого нужно определить функцию, описывающую кривую, а затем использовать интеграл для нахождения объема фигуры, полученной вращением этой кривой вокруг оси.

Существует несколько способов нахождения объема тела вращения в зависимости от геометрической формы кривой и оси вращения. Например, для нахождения объема цилиндра необходимо знать радиус основания и высоту цилиндра. Для нахождения объема конуса необходимо знать радиус основания и высоту конуса. А для нахождения объема шара необходимо знать радиус шара.

ФигураФормула для нахождения объема

Цилиндр	V = πr^2h
Конус	V = (1/3)πr^2h
Шар	V = (4/3)πr^3

Для более сложных фигур, таких как тор или эллипсоид, формулы для нахождения объема могут быть более сложными и требовать более сложных интегралов.

Объем тела вращения — это важный концепт в математике и имеет много применений в физике, инженерии и других научных областях. Нахождение объема тела вращения является одной из основных задач математического анализа и требует хорошего знания интегрального и дифференциального исчисления.