Математика как найти площадь

Узнайте, как вычислить площадь различных геометрических фигур с помощью математических формул и методов. Научитесь находить площадь прямоугольника, круга, треугольника, трапеции и других фигур. Наши подробные инструкции и примеры помогут вам легко и точно определить площадь.

Одной из основных задач математики является нахождение площади различных геометрических фигур. Площадь – это величина, которая показывает, сколько плоскости занимает фигура. Знание площади фигур необходимо во многих областях науки и практики, начиная от строительства и геодезии, до архитектуры и дизайна.

Существует множество различных методов для нахождения площади фигур. Некоторые из них просты и требуют лишь простых математических операций, таких как сложение и умножение. Другие методы более сложны и требуют использования специфических формул и алгоритмов. В этой статье мы рассмотрим основные методы для нахождения площади различных фигур.

Формула площади

Одним из самых простых методов для нахождения площади фигур является использование формулы. Формула площади – это математическое выражение, которое позволяет вычислить площадь фигуры. Каждая фигура имеет свою уникальную формулу, которая зависит от ее геометрических свойств.

К примеру, для прямоугольника площадь можно найти, умножив длину на ширину. Для круга площадь можно вычислить, умножив квадрат радиуса на число пи. Для треугольника можно использовать формулу, основанную на длинах его сторон и высоте.

Помимо использования формул, существует также несколько графических методов для нахождения площади фигур. Например, метод разбиения фигуры на более простые фигуры, площадь которых уже известна. Этот метод основан на принципе аддитивности площади – площадь сложной фигуры равна сумме площадей ее составляющих частей.

Методы математики для вычисления площади фигур

Вот некоторые из основных методов для вычисления площади:

1. Метод для вычисления площади прямоугольника. Площадь прямоугольника можно найти, умножив длину его сторон.
2. Метод для вычисления площади квадрата. Площадь квадрата можно найти, возведя в квадрат длину его стороны.
3. Метод для вычисления площади треугольника. Площадь треугольника можно найти, умножив половину произведения длины одной из его сторон на высоту, опущенную к этой стороне.
4. Метод для вычисления площади круга. Площадь круга можно найти, умножив квадрат радиуса на число Пи (π).
5. Метод для вычисления площади эллипса. Площадь эллипса можно найти, умножив произведение полуосей на число Пи (π).

Это лишь некоторые из методов, которые используются для вычисления площади различных фигур. В зависимости от формы и характеристик фигуры, может быть применен иной метод. Важно понимать, что вычисление площади фигуры является важным элементом математики и находит применение в различных областях, включая геометрию, физику и инженерию.

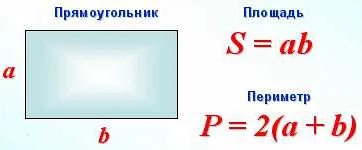
Формула для вычисления площади прямоугольника

Для вычисления площади прямоугольника используется простая формула: площадь равна произведению длины одной стороны на длину другой стороны.

Формула выглядит следующим образом:

• Пусть a — длина одной стороны прямоугольника.
• Пусть b — длина другой стороны прямоугольника.
• Тогда площадь прямоугольника вычисляется по формуле: S = a * b.

Например, если длина одной стороны прямоугольника равна 5 см, а длина другой стороны равна 10 см, то площадь прямоугольника будет равна 5 см * 10 см = 50 см2.

Как найти площадь квадрата

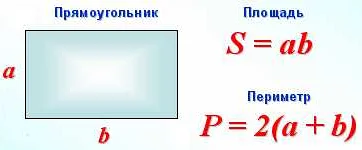
Формула для нахождения площади квадрата выглядит следующим образом:

Площадь = сторона * сторона

Где:

• Площадь — площадь квадрата;
• сторона — длина одной стороны квадрата.

Для примера, если сторона квадрата равна 5 сантиметров, то площадь можно найти, умножив 5 на 5:

Площадь = 5 см * 5 см = 25 см²

Таким образом, площадь квадрата равна 25 квадратным сантиметрам.

Формула для вычисления площади треугольника

Формула для вычисления площади треугольника зависит от известных данных о фигуре. Один из способов вычисления площади треугольника основан на известной длине его основания и высоте, опущенной на эту основание.

Формула для вычисления площади треугольника:

Площадь = (Основание * Высота) / 2

В этой формуле «Основание» представляет собой длину одной из сторон треугольника, а «Высота» – расстояние от этой стороны до противоположного ей угла, опущенное перпендикулярно к этой стороне.

Применение этой формулы позволяет с легкостью вычислить площадь треугольника, зная его основание и высоту. Таким образом, для нахождения площади треугольника достаточно знать длину одной из его сторон и высоту, опущенную на эту сторону.

Как найти площадь круга

Площадь круга можно найти, используя формулу:

S = π * r^2

где S — площадь круга, π (пи) — математическая константа, примерное значение которой равно 3,14, а r — радиус круга.

Для расчета площади круга необходимо знать его радиус. Радиус — это расстояние от центра круга до любой точки на его окружности.

Чтобы найти площадь круга, нужно возвести радиус в квадрат и умножить на число π. Полученное число будет являться площадью круга.

Например, если радиус круга равен 5 см, то площадь круга будет:

S = 3,14 * 5^2 = 3,14 * 25 = 78,5 см^2

Также стоит отметить, что площадь круга всегда будет выражаться в квадратных единицах, таких как сантиметры квадратные (см^2) или метры квадратные (м^2).

Методы вычисления площади трапеции

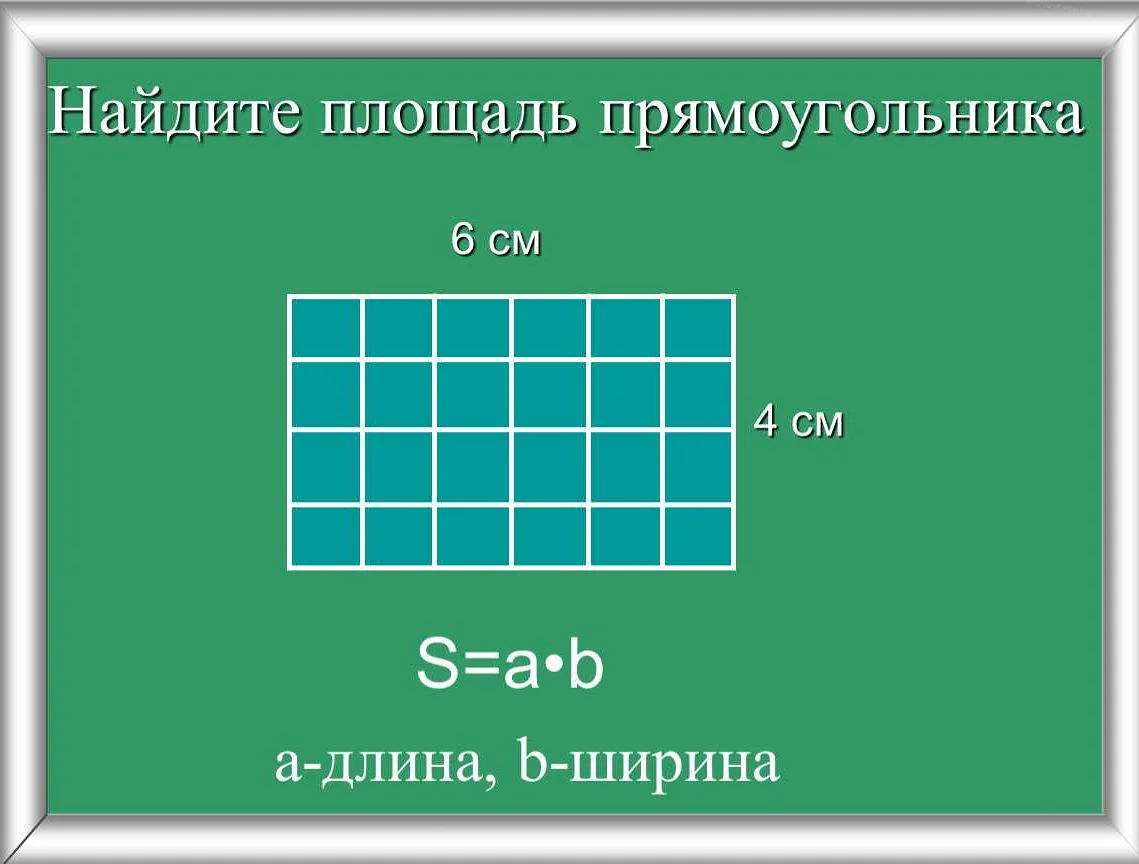
1. Формула площади через основания и высоту: Если у нас есть два основания трапеции (большее и меньшее) и высота, то площадь можно вычислить по формуле S = ((a + b) / 2) * h, где a и b — основания, h — высота трапеции.

2. Формула площади через основания и угол: Если у нас есть два основания трапеции (большее и меньшее) и угол между ними, то площадь можно вычислить по формуле S = (a^2 — b^2) * tan(α) / 4, где a и b — основания, α — угол между ними.

3. Формула площади через диагонали: Если у нас известны диагонали трапеции, то площадь можно вычислить по формуле S = (d1 + d2) * h / 2, где d1 и d2 — диагонали, h — расстояние между ними (высота).

Использование одного из этих методов позволяет нам вычислить площадь трапеции, если у нас имеются соответствующие данные.

Как найти площадь параллелограмма

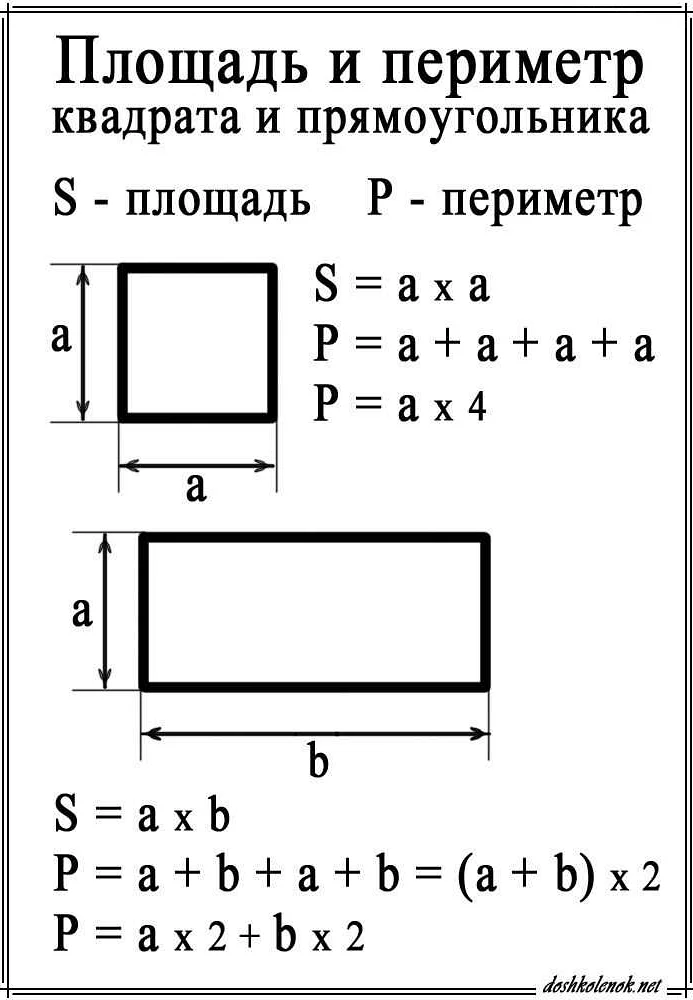
Площадь = основание * высота

Основание параллелограмма — это любая из его сторон, которая является основной. Высота параллелограмма — это перпендикуляр, опущенный из вершины параллелограмма на основание.

Чтобы найти площадь параллелограмма, нужно знать длину одной из его сторон (основание) и длину перпендикуляра, опущенного на это основание (высота).

Пример:

Допустим, у нас есть параллелограмм со сторонами 5 см и высотой 3 см.

Подставляем значения в формулу:

Площадь = 5 см * 3 см = 15 см²

Таким образом, площадь данного параллелограмма равна 15 квадратных сантиметров.

Формула для вычисления площади эллипса

Один из способов вычисления площади эллипса заключается в использовании формулы:

Площадь эллипса равна произведению числа π (пи) на полуоси a и b, где a и b — полуоси эллипса:

S = π * a * b

Эта формула позволяет найти площадь эллипса, зная его полуоси. Полуоси эллипса представляют собой расстояния от центра эллипса до края фигуры вдоль главных осей эллипса.

Обратите внимание, что π — это математическая константа, которая приближенно равна 3.14159. Ее значение можно использовать для точного вычисления площади эллипса.

Вопрос-ответ:

Как найти площадь прямоугольника?

Для нахождения площади прямоугольника необходимо умножить длину одной из его сторон на длину другой стороны.

Как найти площадь круга?

Чтобы найти площадь круга, нужно умножить квадрат радиуса на число π (пи). Формула для нахождения площади круга: S = π * r², где S — площадь, r — радиус.

Как найти площадь треугольника?

Для нахождения площади треугольника можно использовать несколько разных формул, в зависимости от данных, которые у нас есть. Если у нас есть известны длины сторон треугольника, можно воспользоваться формулой Герона: S = √(p * (p — a) * (p — b) * (p — c)), где S — площадь, p — полупериметр треугольника, a, b, c — длины сторон. Если у нас известны длины основания и высоты треугольника, можно воспользоваться формулой: S = (a * h) / 2, где S — площадь, a — длина основания, h — высота треугольника.

Как найти площадь параллелограмма?

Для нахождения площади параллелограмма необходимо умножить длину одной из его сторон на высоту, опущенную на эту сторону.

Как найти площадь трапеции?

Для нахождения площади трапеции необходимо сложить длины оснований, умножить сумму на высоту, опущенную на основания, и разделить полученное значение на 2.

Методы вычисления площади ромба

Площадь ромба можно вычислить различными способами. Вот несколько основных методов:

1. Формула через стороны:

Площадь ромба равна произведению его диагоналей, деленному на 2.

S = (d1 * d2) / 2

2. Формула через сторону и высоту:

Площадь ромба равна произведению его стороны на высоту, деленному на 2.

S = a * h / 2

3. Формула через угол и сторону:

Площадь ромба равна произведению квадрата одной из его сторон на синус угла между этой стороной и любой другой стороной.

S = a^2 * sin(α)

Выбор метода для вычисления площади ромба зависит от того, какие данные у вас есть о фигуре. Если известны стороны, можно использовать первую или вторую формулу. Если известны углы и одна из сторон, можно воспользоваться третьей формулой.

Видео по теме: