То что приходится извлекать математику чтобы посчитать площадь криволинейных трапеций 8 букв

Узнайте, как вычислить площадь криволинейных трапеций, используя математику, в этой статье. Решение данной задачи требует знания определенных математических формул и методов вычислений. Получите необходимые знания и научитесь применять их для расчета площади криволинейных трапеций размером 8 букв.

Криволинейная трапеция — это фигура, которая имеет две параллельные стороны и две непараллельные стороны, обе из которых имеют кривые формы. Вычисление площади криволинейной трапеции является важной задачей в математике. Для этого необходимо знать уравнение кривой, которая определяет форму непараллельных сторон.

Для вычисления площади криволинейной трапеции используется интеграл. Сначала необходимо разделить криволинейную трапецию на маленькие элементы, наклонные к оси x. Затем вычисляется длина каждого элемента и его высота, которая является разностью значений функции для двух кривых сторон. После этого интегрируется произведение длины элемента и его высоты по оси x в пределах от одной кривой стороны до другой. Результатом является площадь криволинейной трапеции.

Пример:

Пусть у нас есть криволинейная трапеция с непараллельными сторонами, определяемыми уравнениями y = x^2 и y = 2x. Чтобы вычислить площадь этой трапеции, мы разделим ее на маленькие элементы dx, наклонные к оси x. Длина каждого элемента dx будет равна самому элементу dx, а высота будет равна разности значений функций y = x^2 и y = 2x.

Затем мы интегрируем произведение длины элемента и его высоты по оси x в пределах от точки пересечения двух функций до конца трапеции. Результатом интегрирования будет площадь криволинейной трапеции.

Криволинейные трапеции: определение и свойства

Для криволинейных трапеций характерно следующее свойство:

1. Базы криволинейной трапеции — это параллельные прямые линии, которые являются ее верхней и нижней основаниями.

2. Высота криволинейной трапеции — это перпендикуляр, проведенный из вершины криволинейной стороны к одному из оснований.

3. Стороны криволинейной трапеции — это отрезки прямых линий, которые соединяют соответствующие вершины оснований.

4. Углы криволинейной трапеции — это углы, образованные боковыми сторонами и основаниями.

Площадь криволинейной трапеции может быть вычислена с использованием формулы:

S = ((a + b) * h) / 2

где S — площадь, a и b — длины оснований, h — высота.

Основные понятия криволинейных трапеций

Основания криволинейной трапеции — это параллельные прямые линии, которые не пересекаются и образуют прямоугольник или прямоугольную трапецию, когда боковые стороны являются отрезками.

Боковые стороны криволинейной трапеции — это криволинейные линии, которые соединяют соответствующие концы оснований.

Высота криволинейной трапеции — это перпендикуляр, опущенный из одного основания на другое основание или его продолжение.

Площадь криволинейной трапеции — это величина, равная произведению полусуммы оснований на высоту.

Формула для вычисления площади криволинейной трапеции: S = (a + b) * h / 2, где a и b — длины оснований, h — высота.

Пример вычисления площади криволинейной трапеции:

Дано: криволинейная трапеция с основаниями a = 6 см и b = 10 см, высота h = 8 см.

Решение: подставляем значения в формулу площади криволинейной трапеции: S = (6 + 10) * 8 / 2 = 80 см².

Ответ: площадь криволинейной трапеции равна 80 см².

Формула для вычисления площади криволинейных трапеций

Площадь криволинейной трапеции может быть вычислена с использованием формулы:

1. Разделить криволинейную трапецию на прямоугольный треугольник и прямоугольник.
2. Вычислить площади этих двух фигур по отдельности.
3. Сложить полученные площади, чтобы получить общую площадь криволинейной трапеции.

Формула для вычисления площади прямоугольного треугольника:

S = (a * h) / 2,

где S — площадь треугольника, a — длина основания треугольника, h — высота треугольника.

Формула для вычисления площади прямоугольника:

S = a * b,

где S — площадь прямоугольника, a — длина одной из сторон прямоугольника, b — длина другой стороны прямоугольника.

После вычисления площадей треугольника и прямоугольника, сложите их, чтобы получить общую площадь криволинейной трапеции.

Пример вычисления площади криволинейной трапеции

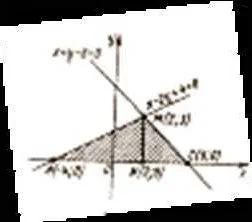
Площадь криволинейной трапеции можно вычислить с использованием определенного интеграла. Для этого необходимо знать уравнение кривой, ограничивающей трапецию, а также координаты точек, где эта кривая пересекает ось абсцисс.

Предположим, что у нас есть криволинейная трапеция, ограниченная кривой y = f(x), осью абсцисс и двумя вертикальными прямыми x = a и x = b. Площадь такой трапеции можно вычислить по следующей формуле:

S = ∫ab f(x) dx,

где S — площадь криволинейной трапеции, f(x) — уравнение кривой, a и b — координаты точек пересечения кривой с осью абсцисс.

Для вычисления интеграла можно использовать различные методы, такие как методы численного интегрирования или методы аналитического интегрирования, в зависимости от функции f(x).

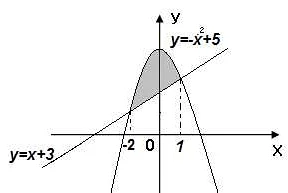
Например, рассмотрим криволинейную трапецию, ограниченную кривой y = x2, осью абсцисс и прямыми x = 0 и x = 2. Для вычисления площади такой трапеции, мы можем использовать следующую формулу:

S = ∫02 x2 dx.

Интегрируя это выражение, получим:

S = [(1/3)x3]02 = (1/3)(23 — 03) = 8/3.

Таким образом, площадь криволинейной трапеции, ограниченной кривой y = x2, осью абсцисс и прямыми x = 0 и x = 2, равна 8/3.

Связь площади криволинейных трапеций с другими фигурами

Площадь криволинейной трапеции может быть связана с другими фигурами, такими как прямоугольник, параллелограмм и прямоугольный треугольник.

Площадь криволинейной трапеции может быть вычислена с помощью следующей формулы:

S = (a + b) * h / 2

где a и b — длины оснований трапеции, а h — высота трапеции.

Если представить криволинейную трапецию в виде разрезанного прямоугольника, то площадь такой трапеции будет равна площади прямоугольника, из которого вычитается площадь двух прямоугольных треугольников.

Также, если представить криволинейную трапецию в виде разрезанного параллелограмма, то площадь такой трапеции будет равна площади параллелограмма, из которой вычитается площадь прямоугольника, состоящего из двух прямоугольных треугольников.

Таким образом, площадь криволинейной трапеции может быть вычислена, используя свойства и связи с другими фигурами.

Практическое применение площади криволинейных трапеций

1. Архитектура и строительство:

Площадь криволинейной трапеции может быть использована для вычисления площади крыши здания, которая имеет нестандартную форму. Это позволяет архитекторам и инженерам определить необходимое количество материалов для строительства и рассчитать затраты на проект.

2. Геодезия и картография:

Площадь криволинейных трапеций используется при измерении площади земельных участков и составлении карт. Это позволяет определить площадь участка земли, его границы и взаимное расположение соседних участков.

3. Физика и инженерия:

Площадь криволинейной трапеции может быть применена при расчете площади поверхности тела, имеющего сложную форму. Это особенно важно при изучении теплообмена, массообмена или расчете площади поверхности радиатора.

4. Экономика и финансы:

Площадь криволинейной трапеции может быть использована для оценки объема производства товаров или услуг. Это позволяет более точно рассчитать стоимость производства и прогнозировать прибыльность бизнеса.

Выводящиеся из площади криволинейных трапеций формулы могут быть использованы для решения различных задач и оптимизации процессов в различных областях науки и промышленности.

Связь между площадью криволинейных трапеций и математикой

Интеграл является основным инструментом математического анализа и позволяет находить площадь под кривой. Для вычисления площади криволинейной трапеции необходимо взять определенный интеграл от функции, описывающей верхнюю границу трапеции, вычесть определенный интеграл от функции, описывающей нижнюю границу трапеции, и умножить полученную разность на ширину трапеции.

Понимание математических концепций и умение применять их в вычислениях позволяет нам определить площадь криволинейной трапеции. Это является важным умением не только в математике, но и в других научных и технических областях, где требуется анализ и измерение площадей фигур.

Ширина трапецииВерхняя границаНижняя границаРазность границПлощадь трапеции

h

f(x)

g(x)

f(x) — g(x)

(f(x) — g(x)) * h

В таблице представлены основные формулы для вычисления площади криволинейной трапеции. Ширина трапеции обозначается символом h, верхняя граница функцией f(x), нижняя граница функцией g(x), разность границ — (f(x) — g(x)), а площадь трапеции — (f(x) — g(x)) * h. Здесь x — переменная, от которой зависят границы трапеции.

Таким образом, математика предоставляет нам инструменты и формулы для вычисления площади криволинейных трапеций. Это позволяет нам более точно и систематично определять площадь фигур и применять эту информацию в различных областях, где требуется работа с геометрическими фигурами.

Вопрос-ответ:

Как вычислить площадь криволинейной трапеции?

Для вычисления площади криволинейной трапеции необходимо разбить ее на бесконечно маленькие прямоугольники, вычислить площадь каждого прямоугольника и сложить их. Затем полученную сумму суммировать от начальной точки до конечной точки кривой.

Как найти площадь криволинейной трапеции, если известны ее верхнее и нижнее основания?

Если известны верхнее и нижнее основания криволинейной трапеции, то площадь можно найти, используя формулу площади трапеции: S = (a + b) * h / 2, где a и b — верхнее и нижнее основания, а h — высота трапеции.

Как найти площадь криволинейной трапеции, если известны ее боковые стороны?

Если известны боковые стороны криволинейной трапеции, то площадь можно найти, используя формулу площади криволинейной трапеции: S = (a + b) * h / 2, где a и b — боковые стороны, а h — высота трапеции.

Как найти площадь криволинейной трапеции, если известны ее диагонали?

Если известны диагонали криволинейной трапеции, то площадь можно найти, используя формулу площади трапеции: S = (a + b) * h / 2, где a и b — диагонали, а h — высота трапеции.

Математическая формула для определения площади криволинейных трапеций

Площадь криволинейных трапеций можно вычислить с помощью следующей математической формулы:

ФормулаОписание

S = ½(a + b)h

где S — площадь криволинейной трапеции, a и b — длины параллельных сторон трапеции, h — высота трапеции

Для вычисления площади криволинейных трапеций необходимо знать длины параллельных сторон трапеции и её высоту. Длины сторон и высоту можно измерить с помощью геометрических инструментов или получить из условия задачи.

Применение данной формулы позволяет находить площадь криволинейных трапеций в различных геометрических задачах, что является важным инструментом в математике.

Видео по теме: