Площадь квадрата 4 класс математика как найти

Научитесь находить площадь квадрата в 4 классе посредством простых математических операций. Узнайте, как измерить стороны квадрата и применить формулу для нахождения его площади. Полезная информация и примеры расчетов.

Квадрат — это геометрическая фигура, имеющая четыре равные стороны и четыре прямых угла. Площадь квадрата — это величина, которая показывает, сколько квадратных единиц площади занимает этот квадрат. Научиться находить площадь квадрата в математике очень важно, так как это базовое знание, которое понадобится в дальнейшем изучении геометрии и алгебры.

Формула для нахождения площади квадрата очень проста. Площадь квадрата равна квадрату длины его стороны. Если сторона квадрата равна a, то его площадь обозначается символом S и вычисляется по формуле: S = a². Например, если длина стороны квадрата равна 5 см, то его площадь будет равна 25 квадратных сантиметров.

Нахождение площади квадрата в математике может быть использовано в различных задачах. Например, если нам известна площадь квадрата и нужно найти длину его стороны, то можно воспользоваться обратной операцией — извлечением квадратного корня. Если известна площадь S, то длина стороны квадрата a равна квадратному корню из S.

Знание формулы для нахождения площади квадрата открывает возможность решать различные задачи, связанные с измерением и геометрией. Помимо простого вычисления площади, эти знания могут быть применены в реальной жизни, например, при строительстве или ремонте, расчете площади помещения, а также в других сферах, где нужно измерять и сравнивать площади различных объектов.

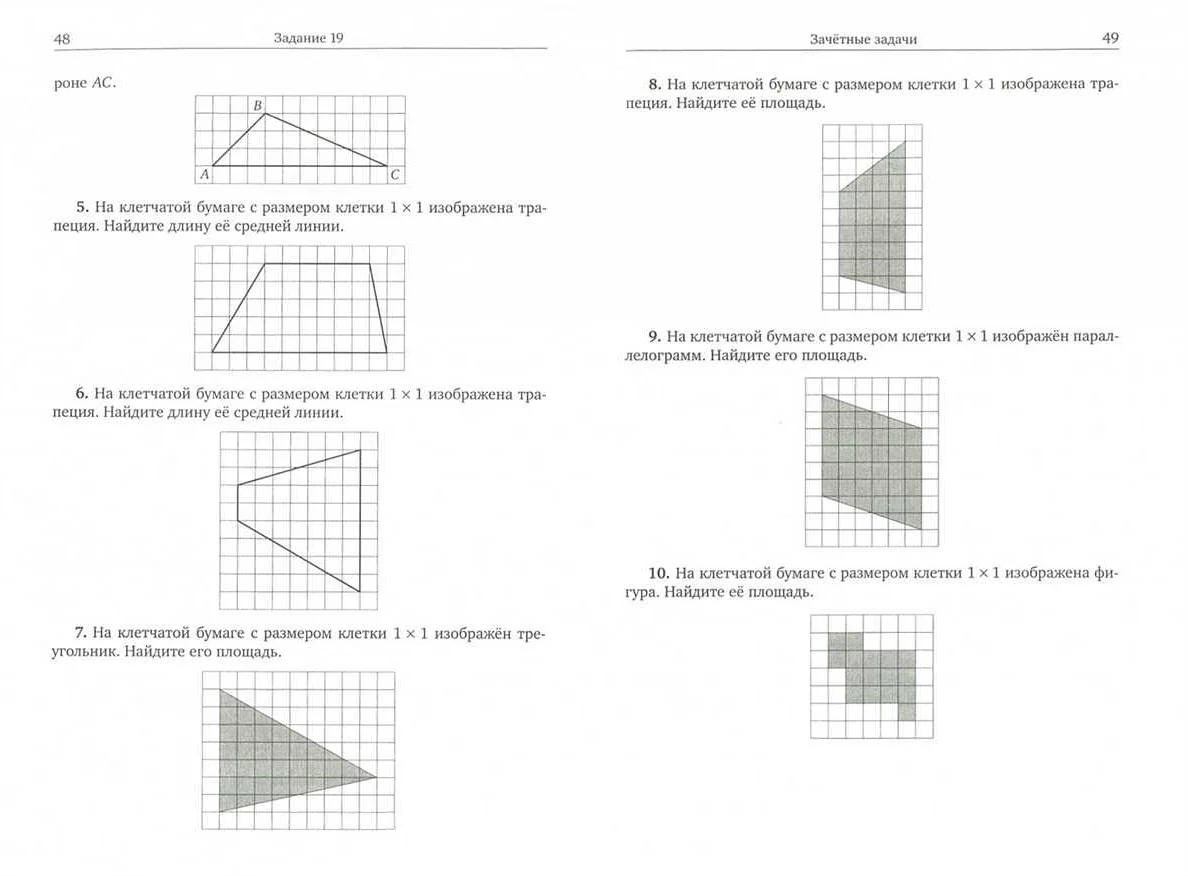
Что такое площадь квадрата?

Для того чтобы найти площадь квадрата, необходимо знать длину одной его стороны. Площадь квадрата вычисляется по формуле: Площадь = сторона × сторона или, в более простой форме, Площадь = сторона2.

Например, если сторона квадрата равна 5 сантиметрам, то его площадь будет равна 5 см × 5 см = 25 см2. Если сторона квадрата равна 3 метрам, то его площадь будет равна 3 м × 3 м = 9 м2.

Понимание площади квадрата важно для решения различных задач, связанных с геометрией и практическими применениями. Например, зная площадь квадрата, можно определить, сколько плиток нужно для покрытия его поверхности или сколько ткани нужно для пошива квадратной подушки.

Способы нахождения площади квадрата

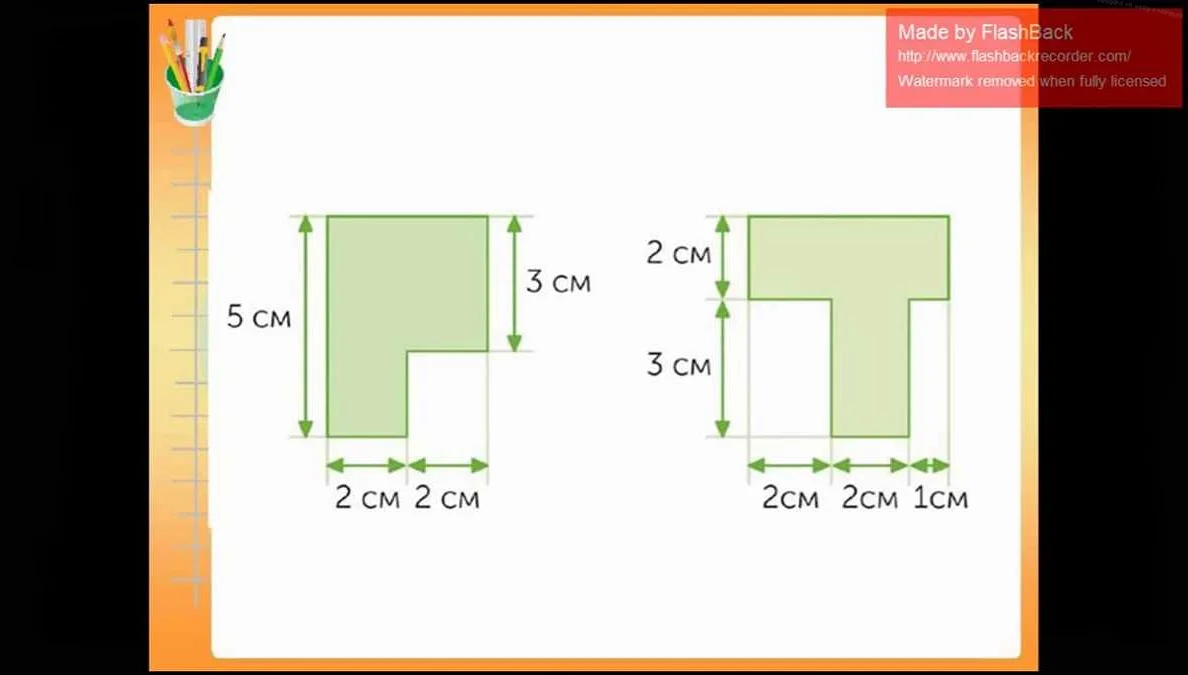
Для того чтобы найти площадь квадрата, можно воспользоваться несколькими способами.

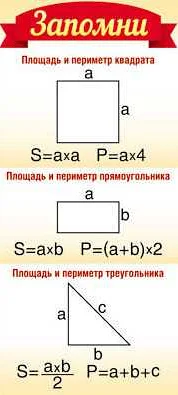
1. Формула площади квадрата: Площадь квадрата можно найти, умножив длину одной из его сторон на саму себя. То есть, если сторона квадрата равна a, то его площадь равна a2.

2. Измерение стороны квадрата: Если известна длина стороны квадрата, то площадь можно найти, умножив эту длину на себя.

3. Квадратная сетка: Если нарисовать квадратную сетку, то площадь квадрата можно найти, посчитав количество квадратных клеток, на которые он разбивается.

Зная эти способы, можно легко найти площадь квадрата и использовать эту информацию в решении математических задач.

Сторона квадрата

Чтобы найти площадь квадрата, нужно возвести длину его стороны в квадрат, то есть умножить ее на саму себя. Формула для нахождения площади квадрата выглядит следующим образом:

Площадь квадрата (S)

=

Сторона (a)

×

Сторона (a)

=

a2

Например, если сторона квадрата равна 5 см, то его площадь будет:

Площадь квадрата (S)

=

5 см

×

5 см

=

25 см2

Таким образом, площадь квадрата с длиной стороны 5 см равна 25 квадратным сантиметрам.

Формула для нахождения площади

Площадь квадрата можно найти, используя простую формулу. Для этого нужно знать длину стороны квадрата и умножить ее на саму себя.

Формула для нахождения площади квадрата выглядит следующим образом:

Формула:

Площадь = Длина стороны × Длина стороны

Например, если длина стороны квадрата равна 5 см, то площадь можно найти по формуле:

Формула:

Площадь = 5 см × 5 см = 25 см²

Таким образом, площадь квадрата с длиной стороны 5 см будет равна 25 квадратным сантиметрам.

Примеры решения

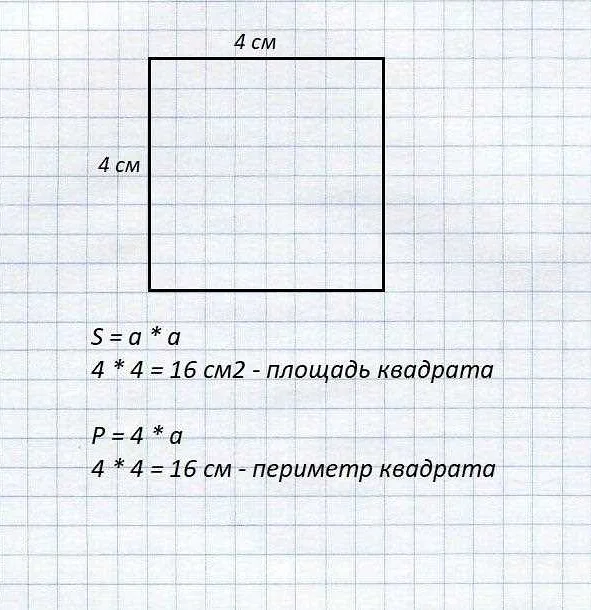
Для того чтобы найти площадь квадрата, нужно знать длину одной из его сторон. Давайте рассмотрим несколько примеров:

Пример 1:

Пусть длина стороны квадрата равна 5 см. Чтобы найти площадь, нужно возвести эту длину в квадрат:

Площадь = 5 см × 5 см = 25 см²

Пример 2:

Пусть длина стороны квадрата равна 8 м. Тогда площадь будет:

Площадь = 8 м × 8 м = 64 м²

Пример 3:

Пусть длина стороны квадрата равна 12 дм. Вычислим площадь:

Площадь = 12 дм × 12 дм = 144 дм²

Важно помнить, что площадь квадрата всегда выражается в квадратных единицах, таких как квадратные сантиметры (см²), квадратные метры (м²) или квадратные дециметры (дм²).

Видео по теме:

Вопрос-ответ:

Как найти площадь квадрата?

Чтобы найти площадь квадрата, нужно умножить длину одной стороны на другую сторону.

Какую формулу использовать для нахождения площади квадрата?

Формула для нахождения площади квадрата: S = a * a, где S — площадь, а — длина стороны.

Какие данные нужны, чтобы найти площадь квадрата?

Для нахождения площади квадрата нужно знать длину одной его стороны.

Чему равна площадь квадрата, если его сторона равна 5 см?

Если сторона квадрата равна 5 см, то его площадь будет равна 25 квадратных сантиметров.

Как найти площадь квадрата, если известен его периметр?

Если известен периметр квадрата, то можно найти его сторону, а затем по этой стороне найти площадь, используя формулу S = a * a.

Пример 1

Допустим, у нас есть квадрат со стороной 5 см. Чтобы найти площадь этого квадрата, нужно умножить длину одной из его сторон на саму себя: 5 см × 5 см.

5 см × 5 см = 25 квадратных сантиметров.

Таким образом, площадь квадрата со стороной 5 см равна 25 квадратным сантиметрам.

Пример 2

У нас есть квадрат со стороной 5 см. Чтобы найти площадь этого квадрата, нужно умножить длину его стороны на саму себя.

Длина стороны квадрата: 5 см.

Площадь квадрата = 5 см * 5 см = 25 см².