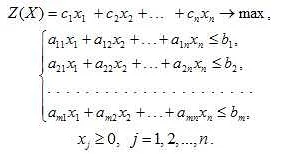Как создать эффективную математическую модель: основные принципы и советы

Как построить математическую модель? Узнайте основные шаги и приемы, которые помогут вам построить правильную и точную модель, на примере решения задачи массового обслуживания.

Математическая модель – это абстрактное и идеализированное представление реальной ситуации или системы в виде математических уравнений и формул. Использование математических моделей широко распространено в науке, бизнесе, производстве и других областях. Создание качественной математической модели – это ключевой этап в построении решений и принятии важных решений.

В этой статье мы рассмотрим 5 шагов, которые помогут вам создать математическую модель с максимальной эффективностью и точностью. Мы расскажем о том, как проводится исследование объекта, как выбрать правильные параметры, в каком виде должны быть выражены переменные и другие важные аспекты формирования математической модели.

Независимо от того, в какой области вы работаете, эти пять шагов помогут вам убедиться, что ваша модель будет точной, надежной, а подход к ее созданию – методически правильным. Это поможет сохранить время и ресурсы, а также улучшить результаты вашей работы.

Шаг 1. Определение цели моделирования

Перед тем, как начать разработку математической модели, необходимо определить конечную цель, которую вы хотите достигнуть. Цель моделирования может быть различной и зависит от конкретной задачи, которую вы хотите решить с помощью модели.

Некоторые из возможных целей моделирования:

• Прогнозирование динамики определенного процесса или явления;
• Оптимизация работы системы или процесса;
• Идентификация взаимосвязей между различными параметрами процесса;
• Установление причинно-следственных связей между различными явлениями;
• Анализ рисков при принятии решений;
• Проектирование новых систем или процессов.

Выбор конечной цели позволяет определить направление и границы разработки модели, выбрать методы и инструменты для ее построения и анализа, а также оценить эффективность и качество полученных результатов.

Шаг 2. Сбор и анализ данных

Сбор и анализ данных — это второй критически важный шаг при разработке математической модели. Этот шаг начинается с определения данных, необходимых для составления модели. Необходимо определить, какая информация нужна для идентификации и описания процесса, который вы хотите моделировать.

Собрать данные можно различными способами: использовать уже имеющиеся данные, сделать специальный опыт или задачу для получения необходимой информации, проводить интервью и опросы и многие другие.

Собранные данные необходимо тщательно проанализировать. Оцените качество и достоверность данных, проверьте данные на полноту и корректность, исключите ошибки и пропущенные значения. При анализе данных используйте статистические методы, графические представления, таблицы и диаграммы для получения полной картины.

По результатам анализа составьте список переменных, которые будут использоваться в модели, определите их значение и связи между ними. Также учитывайте вероятность появления новых данных в будущем.

Сбор и анализ данных — это важный этап, который может занять много времени и усилий. Однако, более тщательный и точный анализ данных позволит создать более точную и полную математическую модель, которая будет более эффективна в решении задач.

Шаг 3. Выбор математической модели

Выбор математической модели является одним из ключевых шагов в разработке математической модели. Здесь требуется определить, какая модель наилучшим образом описывает явление, которое мы хотим исследовать.

На этом этапе необходимо рассмотреть различные доступные модели и оценить их преимущества и недостатки. Необходимо учитывать, насколько точно модель соответствует реальным данным, как она проста в использовании и настройке, и как она масштабируется для работы с различными объемами данных.

Существует множество типов математических моделей, от простых линейных моделей до сложных нелинейных моделей машинного обучения. Кроме того, необходимо учитывать и другие факторы, такие как время, необходимое для обучения модели и время, необходимое для проведения прогнозов и анализа.

Иногда может потребоваться сочетание нескольких моделей для достижения наилучших результатов. В этом случае необходимо провести дополнительный анализ и оценку возможных комбинаций моделей.

Выбор математической модели является важным шагом, который может повлиять на качество итоговой математической модели. Поэтому, следует использовать все доступные инструменты для проведения анализа и выбора наилучшей модели.

Шаг 4. Разработка и тестирование модели

На этом этапе разработчики создают конкретную математическую модель, опираясь на результаты предыдущих этапов. Важно учитывать все особенности системы и задачи, для которой создается модель. При разработке модели используются специализированные программы и инструменты, которые позволяют описать математические зависимости и выполнять необходимые расчеты.

После разработки модели ее необходимо протестировать, чтобы убедиться в ее точности. Для этого используется статистический анализ данных и временные ряды, которые позволяют сравнить результаты моделирования с реальными данными. Если модель не дает достоверных результатов, ее необходимо доработать и исправить ошибки.

Определение точности модели является очень важным шагом, так как от этого зависит ее дальнейшее использование. Если модель дает достоверные результаты, ее можно использовать для прогнозирования и анализа поведения системы в различных условиях.

После успешного тестирования модели, ее можно использовать для решения задач и принятия решений в реальных условиях. Однако, модель необходимо постоянно совершенствовать и обновлять, чтобы она соответствовала актуальным требованиям и условиям.

Таким образом, разработка и тестирование математической модели является сложным и многопроцессным процессом, который требует серьезных знаний в области математики, программирования и статистики. Только правильное выполнение всех шагов гарантирует создание точной и достоверной модели, которая пригодна для использования в реальных условиях.

Шаг 5. Интерпретация и применение результатов моделирования

Интерпретация результатов

После построения математической модели и её запуска на компьютере, полученные результаты необходимо проанализировать и интерпретировать. Результаты могут быть представлены в виде графиков, таблиц, аналитических выводов.

Необходимо определить, насколько степень реальности результатов соответствует поставленной задаче и определить точность модели. Важно оценить потенциальные ошибки и аномалии, которые могут возникнуть в процессе моделирования. Данные могут быть использованы для определения будущих действий в рамках решения проблемы.

Применение результатов

После интерпретации результатов и определения точности модели, можно приступать к их применению. Результаты могут использоваться для:

1. Прогнозирования будущих событий
2. Определения оптимальных решений в рамках проблемы
3. Определения влияния различных факторов на основной процесс
4. Представления решения проблемы в виде рекомендаций, которые могут быть помощными в принятии решений

Правильная интерпретация и применение результатов моделирования могут помочь в решении сложных проблем и принятии оптимальных решений.

Преимущества использования математических моделей

Увеличение точности прогнозирования

С использованием математических моделей можно сократить промежутки времени для прогнозирования будущих событий и прирост точности прогнозов. Модели позволяют определить возможные проявления и сценарии будущих событий на основании постоянно анализируемой информации.

Сокращение времени и затрат на исследования

Разработка математической модели решает проблему необходимости проводить длительные и дорогостоящие исследования. Модель позволяет внести изменения и получить результаты на основании новых данных без необходимости вывода результатов в природе, в лаборатории или на производстве.

Анализ сложных систем и процессов

Использование математических моделей при работе с сложными системами и процессами позволяет описать их с помощью простых уравнений и формул, что делает решение проблемы более удобным и эффективным.

Повышение уровня качества продукции и услуг

С помощью использования моделей можно получать информацию о влиянии наличия дефектов и их причин на производственный процесс. Это позволяет организовать повышение качества продукции и услуг, снижение производственных затрат и потребления ресурсов.

Объективизация процесса принятия решений

Математические модели предоставляют объективную основу для принятия решений, обеспечивая аргументированный подход к принятию решений. Они также могут быть использованы в качестве основы для установления нормативов и регуляций, связанных с производственными процессами.

Улучшение координации действий и оптимизация процессов

Основа математических моделей – анализ данных – обеспечивает варианты координации и оптимизации действий на основе постоянно приближающейся к реальности информации. Это помогает свести к минимуму ошибки и негативные влияния на процессы.

Основные типы математических моделей

Математическая модель – это абстрактное представление о работе объекта или явления, которое используется для проведения исследований и прогнозирования его развития в будущем. Существует несколько основных типов математических моделей, которые в разной степени подходят для конкретных задач.

Аналитические модели – это модели, которые создаются на основе точного анализа объекта или явления и строятся с помощью математических уравнений. Они позволяют получить точные решения и прогнозы, но требуют высокого уровня математической подготовки и возможности проводить сложные вычисления.

Статистические модели – это модели, которые построены на основе сбора и обработки статистических данных. Они позволяют проводить анализ вероятностных явлений и прогнозировать вероятность появления определенных событий в будущем. Однако, они не всегда гарантируют точность результатов и могут быть ограничены масштабом исследований.

Имитационные модели – это модели, которые создаются на основе имитации процессов и выбора решений в условиях неопределенности. Они позволяют проводить эксперименты с объектом или явлением в условиях, которые сложно или невозможно воспроизвести в реальности. Они пользуются популярностью в исследованиях экономических или социальных явлений.

Графические модели – это модели, которые использованы на основе визуального анализа объекта или явления. Они позволяют лучше понять структуру, связи и зависимости между элементами объекта или явления. Они обладают высокой наглядностью и могут быть использованы для презентаций и объяснения сложных концепций.

Нейронные сети – это модели, которые имеют конфигурацию, похожую на сеть нейронов в человеческом мозге. Они позволяют проводить анализ больших объемов данных и прогнозировать дальнейшее развитие объекта или явления. Они считаются одними из наиболее современных и развивающихся видах математических моделей.

Инструменты для построения математических моделей

1. Математические языки

Математические языки представляют собой языки программирования, созданные для работы с математическими объектами. Они позволяют быстро и эффективно проводить математические операции и работать с большими объемами данных. Некоторые из наиболее популярных математических языков включают MATLAB, R, Python и Octave.

2. Симуляционное моделирование

Симуляционное моделирование — это метод построения математической модели, который использует компьютерное моделирование для анализа поведения системы. Этот метод может быть особенно полезен при работе с сложными системами, такими как транспортные сети, финансовые рынки и медицинские процессы.

3. Статистические методы

Статистические методы используются для анализа данных и прогнозирования будущих событий на основе существующих данных. Это может включать методы регрессии, анализ временных рядов и машинное обучение. Статистические методы особенно полезны при работе с большими объемами данных, такими как данные клиентов, которые могут использоваться для принятия бизнес-решений.

4. Оптимизация

Оптимизация — это процесс определения оптимального решения при ограниченных ресурсах. Оптимизационные инструменты могут использоваться для поиска оптимальных решений в таких областях, как финансы, инженерия и логистика. Эти инструменты помогают оптимизировать процессы и увеличить эффективность бизнеса.

5. Графические пользовательские интерфейсы

Графические пользовательские интерфейсы представляют собой инструменты, которые позволяют пользователям взаимодействовать с математическими моделями, используя графические элементы. Эти инструменты могут быть особенно полезны при работе с неспециалистами в области математического моделирования, такими как маркетологи и бизнес-аналитики.

Типичные ошибки при разработке математических моделей

Разработка математической модели — это не простая задача, и даже опытные специалисты могут совершать ошибки. Рассмотрим некоторые типичные ошибки, которые следует избегать:

• Неправильная постановка задачи. Необходимо внимательно определить цели и критерии моделирования. Неправильно сформулированная задача может привести к тому, что модель будет неприменима в практических условиях.
• Недостаточное количество данных. Для создания точной и надежной модели нужно иметь достаточное количество данных. Их нехватка может привести к ошибочному решению задачи.
• Проектирование модели на основе недостаточной информации. Если вы используете неполные или неточные данные, то модель также будет неточной. Необходимо собрать максимальное количество информации и тщательно проанализировать ее перед построением модели.
• Использование неправильных математических методов. Необходимо выбирать методы, лучше всего подходящие для решения конкретной задачи. Использование неправильных методов может привести к неверным результатам.
• Недостаточный анализ результатов моделирования. Необходимо тщательно проанализировать результаты моделирования и убедиться, что они соответствуют постановленным задачам и целям.
• Игнорирование неопределенности. Многие модели используются для прогнозирования будущих событий, но необходимо помнить, что будущее всегда неопределенно. Игнорирование неопределенности может привести к неверным результатам.

Вопрос-ответ:

Какие шаги нужно выполнить для успешной разработки математической модели?

В статье описаны 5 основных шагов, которые нужно выполнить: определить цель моделирования, выбрать подходящий математический инструментарий, собрать и обработать данные, построить модель, провести ее верификацию и валидацию.

Как выбрать подходящий математический инструментарий?

Выбор математического инструментария зависит от поставленной задачи и доступности необходимых средств обработки данных. Важно учитывать какие типы данных планируется обрабатывать, а также подходящие методы математического моделирования.

Какие методы математического моделирования существуют?

Существует множество методов математического моделирования, например, линейное программирование, дифференциальные уравнения, метод конечных элементов, байесовский анализ и другие. Выбор методов зависит от поставленной задачи и доступности необходимых средств обработки данных.

Что такое верификация и валидация модели?

Верификация модели — это процесс проверки правильности реализации математической модели. Валидация модели — это проверка соответствия модели реальности. Эти процессы позволяют убедиться в корректности и пригодности модели для использования в реальных задачах.

Какие типы данных нужно собирать для построения математической модели?

Для построения математической модели необходимо собрать данные, связанные с параметрами, влияющими на процесс, который необходимо описать. Например, если моделируется процесс производства, необходимо собрать данные о сырье, оборудовании, персонале и т.д.

Как провести валидацию модели?

Для проведения валидации необходимо сравнить результаты моделирования с данными, полученными в реальности. Если результаты совпадают, можно считать модель валидной и использовать ее для прогнозирования результатов в будущем.

Возможно ли построить модель, если не хватает данных?

Если данных недостаточно, то построение математической модели может быть затруднено или даже невозможно. В таких случаях можно использовать методы экстраполяции, однако результаты моделирования могут быть неточными.

Успешные примеры применения математических моделей в различных отраслях

Математические модели играют важную роль в различных отраслях экономики, финансов, бизнеса и науки. Здесь мы рассмотрим некоторые успешные примеры применения математических моделей в различных отраслях.

Финансы: Математические модели используются для анализа и прогнозирования тенденций на рынке ценных бумаг, определения перспективных инвестиционных проектов и управления рисками в инвестировании. Например, модель Шарпа используется для определения оптимального соотношения между риском и доходностью портфеля.

Производство: Математические модели помогают оптимизировать производственные процессы, увеличивать эффективность использования ресурсов, минимизировать затраты и улучшать качество продукции. Например, модели математического программирования используются для оптимизации поставок и распределения товаров на складах.

Транспорт и логистика: Математические модели используются для оптимизации планирования маршрутов, расписаний рейсов, управления грузопотоками и оптимизации транспортных расходов. Например, модели оптимизации маршрутов автомобильных перевозок позволяют снизить время и затраты на доставку товаров.

Медицина: Математические модели используются для прогнозирования развития заболеваний, оптимизации расписания приемов врача и разработки новых методов диагностики и лечения. Например, модель прогнозирования развития рака молочной железы позволяет определить наиболее эффективную методику лечения для каждой пациентки.

Экология: Математические модели используются для прогнозирования развития экологических кризисов, оптимизации использования природных ресурсов и уменьшения загрязнения окружающей среды. Например, модель водообмена между озером и подземными водами позволяет определить оптимальный режим эксплуатации водохранилища, с учетом минимизации негативного влияния на экосистему.

Видео по теме: