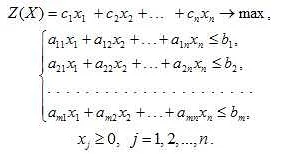Что такое математическая модель задачи: определение и примеры

Математическая модель задачи – это представление реальной задачи в виде математических выражений и формул, которые позволяют анализировать и решать задачу с помощью методов математики и компьютерного моделирования.

В современном мире, без математических моделей трудно представить решение многих задач. Их используют в самых разных отраслях, начиная от физики и медицины, заканчивая экономикой и производством. Математическая модель — это абстрактная модель из определенных математических конструкций, которая отражает реальный процесс.

Построение математической модели задачи — очень важный этап решения задачи, который требует тщательного анализа и понимания проблемы. Правильно составленная математическая модель позволяет найти точное решение задачи, определить зависимость между параметрами и прогнозировать дальнейшее развитие процесса.

Для построения математической модели задачи необходимо провести анализ факторов, влияющих на процесс, разложить его на основные компоненты, определить связи между ними и описать их математическими формулами. При этом важно учитывать все факторы, которые могут повлиять на решение задачи, исключить несущественные и предусмотреть возможность их изменения. Важным этапом является также проверка корректности модели и ее адекватность реальному процессу.

В заключении можно сказать, что математическая модель — это мощный инструмент, который помогает решать сложные задачи и оптимизировать процессы в различных сферах деятельности. Ее построение требует тщательного анализа и понимания проблемы, а правильно составленная модель дает возможность получить точное решение задачи и описать зависимость между параметрами.

Определение понятия «математическая модель задачи»

Математическая модель задачи – это абстрактное описание задачи при помощи математических объектов и операций.

С помощью математических моделей мы можем анализировать, прогнозировать и оптимизировать различные процессы, понимать и изучать различные явления и связи в разных областях, таких как физика, экономика, социология, биология и т.д.

При создании математической модели задачи, сначала определяются ее параметры и переменные, которые могут изменяться в ходе процесса. Затем формулируются гипотетические связи между этими переменными и создаются уравнения или алгоритмы, которые описывают их поведение.

Важно отметить, что математические модели являются упрощенными описаниями реальности и не могут полностью отразить ее сложность и многообразие. Тем не менее, они позволяют получить важные и полезные результаты и предсказания, которые могут быть использованы в решении конкретных задач.

Роли математической модели в решении задач

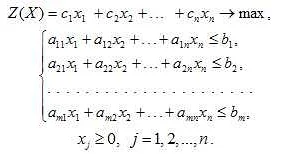
Математическая модель является важным инструментом при решении разнообразных задач. Она позволяет описать процессы, явления и системы в виде формальных математических конструкций, что позволяет более точно анализировать их свойства и поведение.

Одна из главных ролей математической модели в решении задач — это возможность исследования системы в различных условиях и сценариях. Благодаря этому, можно предугадать возможные последствия принятых решений и сделать правильный выбор.

Другая важная роль — это возможность оптимизации системы. Математическая модель позволяет определить наилучшие параметры работы системы, то есть те значения переменных, которые обеспечивают максимальную эффективность и минимальные затраты.

Еще одна роль математической модели — это возможность прогнозировать развитие системы в будущем. На основе анализа ее поведения в прошлом, на основе данных и статистики, можно сделать предсказание ее дальнейшего развития.

В целом, математическая модель — это мощный инструмент, который может использоваться для анализа и решения разных задач, начиная от научных исследований и заканчивая экономическими прогнозами. Конструировать математическую модель не так просто, но если она выполнена правильно, это действительно может быть крайне полезным на практике.

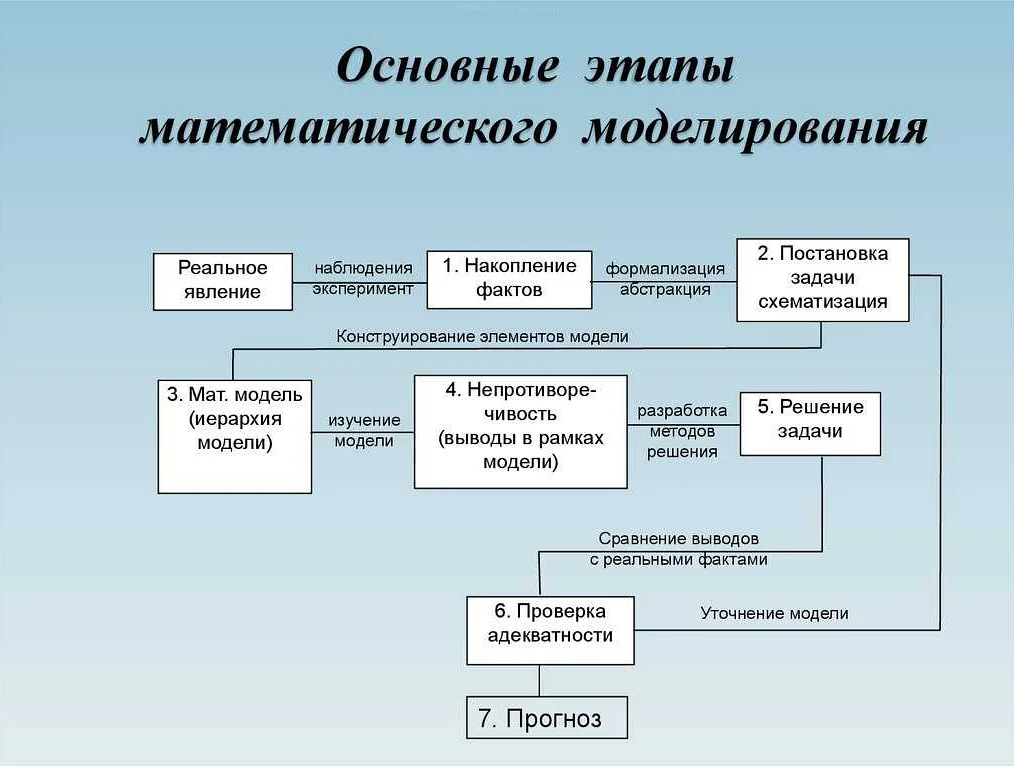
Как строится математическая модель задачи

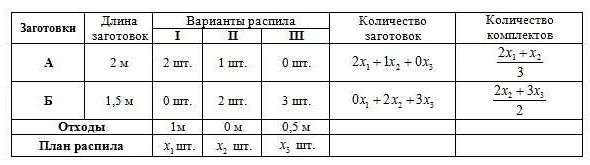
Математическая модель задачи — это абстрактная система, которая описывает реальный процесс в виде символов, формул и уравнений. Для ее построения можно использовать различные математические методы и подходы, в зависимости от типа задачи и целей, которые нужно достичь.

Первым шагом при построении математической модели является определение входных и выходных данных. Входные данные — это параметры, которые воздействуют на систему, а выходные — результат ее работы. Например, в задаче оптимизации производства входными данными могут быть количество ресурсов и количество выпускаемой продукции, а выходными — выручка, прибыль или производительность.

Далее необходимо выбрать математический метод, который будет использоваться при построении модели. Это может быть простейшая арифметика, алгебра, геометрия, теория вероятностей, дифференциальные уравнения и др. Кроме того, можно использовать методы оптимизации, анализа графов, теории игр и другие инструменты для более точного и полного описания системы.

После выбора математического метода происходит формализация модели, т.е. ее описание в виде уравнений, формул и символов. Важно описать каждый этап работы системы и связи между ее компонентами, чтобы получить полную картину процесса.

Наконец, необходимо провести анализ и верификацию модели, чтобы убедиться в ее правильности и соответствии реальному процессу. Также можно провести симуляцию работы системы на компьютере для получения более точных и подробных результатов.

В итоге, математическая модель задачи — это инструмент для более точного и эффективного решения проблем различных областей, от производственного менеджмента до финансов и информационных технологий. Важно правильно определить входные и выходные данные, выбрать подходящий метод и провести анализ модели, чтобы достичь нужных результатов.

Основные шаги в построении математической модели

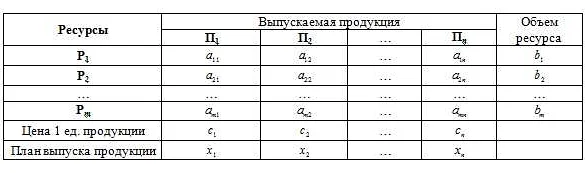
Построение математической модели – это сложный и многолетний процесс, но для начала стоит понимать основные шаги в этом процессе. Ниже мы рассмотрим наиболее важные этапы:

1. Формулирование задачи. Для начала всегда стоит понимать, какую задачу необходимо решить, что именно нужно узнать и какие данные у нас есть. Этот шаг очень важен, поскольку все последующие этапы будут зависеть от правильного понимания задачи.

2. Выбор переменных. После формулирования задачи наша следующая задача – определить переменные, которые будут участвовать в нашей модели. Например, если мы рассматриваем задачу о движении машин, то переменными могут быть скорость, время, расстояние и т.д.

3. Построение соотношений. На этом этапе мы определяем связь между переменными. Например: “расстояние = скорость * время” – это соотношение, которое связывает переменную расстояние с переменными скорости и времени.

4. Выбор метода решения. Как решать задачу – это очень важный вопрос, о котором необходимо задуматься на этапе построения модели. Существует множество методов решения различных задач, но выбор метода будет зависеть от задачи и параметров модели.

5. Проверка и анализ. После построения математической модели необходимо провести ее проверку и анализ. Нужно убедиться в том, что модель корректна и дает верный результат. Если результаты не соответствуют реальности, нужно провести дополнительные исследования и скорректировать модель.

6. Применение. Когда мы убедились в правильности модели, ее можно применять для решения реальных задач. Но важно помнить, что модель – это всего лишь приближение реальной ситуации, и необходимо учитывать все ее ограничения при применении в практике.

Описание математических символов и переменных

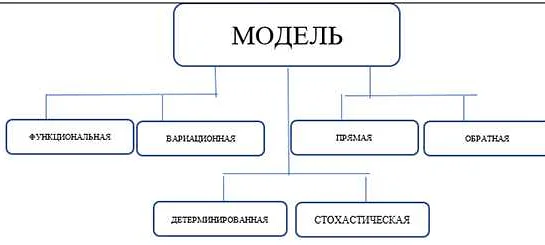
В математических моделях задач, часто используются символы и переменные, чтобы обозначить значения и условия. Вот некоторые общие обозначения:

• x — переменная, представляющая неизвестное значение
• y — переменная, представляющая другое неизвестное значение
• a, b, c — коэффициенты, используемые в уравнениях
• π — математическая константа, представляющая отношение длины окружности к ее диаметру
• √ — символ квадратного корня
• ∞ — символ бесконечности, обозначающий, что значение не имеет ограничения

Кроме того, в математических моделях часто используются символы, чтобы обозначать функции. Некоторые общие обозначения функций включают:

1. f(x) — символ функции, которая принимает значение x и возвращает соответствующее значение f
2. g(x) — другая функция с переменной x
3. sin(x), cos(x), tan(x) — тригонометрические функции
4. log(x) — логарифмическая функция с базой e (экспоненциальной константой)
5. ln(x) — натуральный логарифм функции

Важно знать, как использовать эти символы и переменные в математических моделях задач, чтобы точно определить условия и значения и решить задачу.

Составление уравнений и неравенств

Составление уравнений и неравенств является крайне важным этапом при создании математической модели задачи. Эти математические выражения помогают описать условия, которые необходимо удовлетворить для решения задачи.

Уравнения и неравенства могут быть составлены на основе данных, которые известны о задаче. Например, для задачи о поиске площади прямоугольника можно составить уравнение: S = a * b, где S — площадь прямоугольника, a и b — длины его сторон.

Неравенства могут использоваться, когда нужно ограничить значение некоторой переменной. Например, при решении задачи о максимальной загрузке грузовика, можно составить неравенство: m

При составлении уравнений и неравенств следует учитывать особенности задачи и правильно интерпретировать условия, для того чтобы созданная модель описывала именно решаемую задачу.

Для информативности и удобства также можно использовать таблицы, списки и выделение текста жирным или курсивом. Например:

• Уравнение: S = a * b, где S — площадь прямоугольника, a и b — длины его сторон.
• Неравенство: m

Важно понимать, что составление уравнений и неравенств — это лишь часть процесса создания математической модели. Для получения решения задачи необходимы дополнительные шаги, например, решение системы уравнений или определение минимального или максимального значения функции.

Определение ограничений и условий задачи

Перед построением математической модели задачи необходимо определить все ограничения и условия, которые могут повлиять на решение. Ограничения — это факторы, которые ограничивают допустимые значения переменных в задаче. В свою очередь, условия задачи могут включать в себя как математические формулы, так и нематематические требования.

Прежде всего, необходимо определить все параметры, которые могут использоваться в решении задачи. Затем следует анализировать различные аспекты задачи, например, физические, экономические, временные и т.д. Это может помочь выявить потенциальные ограничения и условия.

Некоторые из распространенных ограничений могут включать в себя допустимые значения переменных, доступные ресурсы, время выполнения задачи или физические ограничения. В свою очередь, условия могут включать в себя требования к точности решения задачи, ограничения на число итераций или другие специфические правила.

Необходимо убедиться, что все ограничения и условия корректно учитываются при построении математической модели задачи. Это позволит избежать ошибок и получить правильное решение.

Построение графической интерпретации математической модели

Графическое представление математической модели — это один из способов визуализировать ее и помочь в понимании того, что происходит в задаче. График может отображать зависимость переменных друг от друга и помочь в обнаружении закономерностей.

Для построения графика нужно определить, какие переменные будут на осях и как они будут зависеть друг от друга. Для этого можно использовать уравнения математической модели и придать им графический смысл.

Если имеется только несколько значений переменных, то можно построить точечную диаграмму, где каждая точка представляет собой один из компонентов переменной. Точечная диаграмма позволяет увидеть связь между переменными и обнаружить возможные закономерности.

Если переменные представляют собой функции, то можно построить график каждой функции и найти точки пересечения. Такой подход позволяет решить задачи оптимизации и найти точки экстремума.

Важно помнить, что графическое представление математической модели — это только один из способов ее визуализации и он может быть не единственным. График не заменит аналитические выкладки и вычисления, поэтому рекомендуется использовать его в сочетании с другими методами моделирования.

Важность проверки и корректировки модели

Строить математическую модель задачи – это сложный процесс, который требует много времени и усилий. Кажется, что когда модель готова, можно сразу переходить к ее решению. Однако, необходима проверка и корректировка модели, чтобы добиться точности и правильности решения.

Проверка модели – это контроль за тем, что выбранные переменные и их взаимосвязи правильно отражают реальность. Необходимо убедиться, что все условия задачи учтены и правильно перенесены в модель. Если есть ошибки или пропущенные условия, решение задачи может оказаться неверным.

Корректировка модели – это процесс внесения изменений в уже готовую модель, если выявлены ошибки или неточности. Иногда может потребоваться изменение исходных данных, чтобы добиться более точного решения задачи.

Важно уделить достаточно времени и внимания проверке и корректировке модели. Это сократит время, потраченное на решение задачи, и поможет добиться более точного результата. Если модель будет неправильной или неточной, это может привести к серьезным последствиям в самых разных областях – от физики и экономики до биологии и медицины.

Примеры решения задач с помощью математических моделей

Моделирование является важным инструментом в решении ряда задач, например:

• Определение общего спроса на продукт. Одна из типичных задач, которую можно решить с помощью математических моделей, состоит в определении общего спроса на продукт. Ответ на этот вопрос может быть полезен для определения цены и объемов производства.
• Оптимизация производственных процессов. Математические модели могут помочь оптимизировать производственные процессы, уменьшить затраты и повысить эффективность производства. Например, вычисление оптимальных объемов производства и распределение ресурсов могут помочь увеличить прибыль компании.
• Прогнозирование будущих результатов. С помощью математических моделей можно предсказать будущие результаты. Это может быть полезно для прогнозирования спроса на продукт, определения бюджета и т.д. Для этого используются различные методы прогнозирования, включая методы временных рядов, регрессионный анализ и моделирование случайных процессов.

Использование математических моделей позволяет принимать решения на основе данных, а не на интуитивном уровне. Это может помочь улучшить результаты и повысить эффективность деятельности.

Вопрос-ответ:

Что такое математическая модель задачи?

Математическая модель задачи — это математическое описание реальной проблемы или явления с помощью уравнений и формул. Это своего рода абстрагирование от сложной реальности, позволяющее работать с проблемой более эффективно.

Зачем нужно строить математические модели задач?

Строить математические модели нужно для того, чтобы с помощью математических методов решить реальную проблему. Модель позволяет изучить проблему в различных условиях и предсказать последствия различных вмешательств в данную ситуацию. Кроме того, моделирование позволяет сэкономить время и средства, которые могли бы быть затрачены на реальные эксперименты.

Какие основные этапы построения математических моделей?

Основные этапы построения математической модели: формулирование вопроса, абстрагирование от реальности, выбор подходящего математического инструмента, построение математической модели, верификация и валидация модели, интерпретация результатов.

Как выбрать подходящий математический инструмент для построения модели?

Выбор математического инструмента зависит от типа задачи. Если решается задача оптимизации, то следует использовать оптимизационный алгоритм. Если задача связана с распределением ресурсов, то подойдет теория игр и др. Важно понимать, какие критерии успеха при решении задачи. На основе этого можно выбрать наиболее подходящий математический инструмент.

Как проверить правильность построенной математической модели?

Проверка математической модели, как правило, осуществляется в несколько этапов. На первом этапе модель может быть проверена на основе аналитических рассуждений и сравнения с известным решением, если таковое имеется. На втором этапе модель может быть проверена на основе статистических методов и экспериментальных данных. На этапе верификации проверяется соответствие модели математическим законам, а на валидации — соответствие модели реальности.

В каких областях наиболее часто применяются математические модели?

Математические модели широко используются в разных областях, включая науку, технологии, экономику, социологию и др. Например, математические модели используются для прогнозирования погоды, эффективности каких-либо методов, моделирования экономических процессов, описания распространения заболеваний и др.

Какие виды математических моделей существуют?

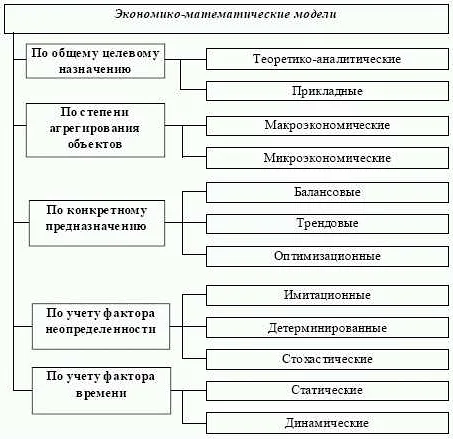
Существует множество видов математических моделей, таких как: статистические модели, дифференциальные уравнения, системы линейных алгебраических уравнений, алгоритмы оптимизации, теория игр, марковские процессы и др. Каждый вид модели имеет свои преимущества и недостатки и может быть более или менее подходящим для данной задачи.

Перспективы использования математических моделей в будущем

Математические модели имеют абсолютно неограниченные перспективы использования в науке, технике и бизнесе. В будущем они будут широко применяться для решения сложных задач и оптимизации процессов.

Например, в медицине математические модели будут использоваться для прогнозирования развития болезней и расчёта оптимальной терапии. В транспортном бизнесе они позволят оптимизировать маршруты и графики движения транспорта. В экономике и финансах — для прогнозирования и анализа рынков.

Одной из главных перспектив математических моделей является их применение в искусственном интеллекте. Моделирование и анализ данных позволят создавать более эффективные и интеллектуальные системы, способные предсказывать поведение объектов и сообщать о прогнозируемых результатах.

С другой стороны, в будущем могут появиться новые виды проблем, которые еще не вероятно решить с использованием существующих математических моделей. Это будет стимулом для разработки новых математических методик и теорий, что в свою очередь приведет к новым открытиям и достижениям в сфере науки и экономики.

Таким образом, перспективы применения математических моделей являются очень обнадеживающими и стимулируют дальнейшее развитие математики и её применения в решении сложных задач и проблем.

Видео по теме: