Сумма в высшей математике как считать
Содержимое
- 1 Сумма в высшей математике как считать
- 1.1 Высшая математика: необходимость правильного подсчета суммы
- 1.2 Основные правила счета в высшей математике
- 1.3 Сложение и вычитание: основные операции
- 1.4 Умножение и деление: правила и примеры
- 1.5 Суммирование бесконечных рядов: приемы и методы
- 1.6 Интегрирование: основные приемы
- 1.7 Примеры высшей математики
- 1.8 Подсчет суммы геометрической прогрессии
- 1.9 Расчет интеграла от функции
- 1.10 Суммирование ряда Фибоначчи
- 1.11 Видео по теме:
Узнайте, как правильно считать и находить суммы в высшей математике. От простых алгебраических выражений до сложных интегралов, мы расскажем вам о различных методах и стратегиях для эффективного вычисления сумм.
Сумма — это одна из основных операций в математике, которая встречается в различных областях науки. В высшей математике суммы играют ключевую роль в алгебре, анализе, комбинаторике и других дисциплинах. Правильное вычисление суммы является важным навыком для решения разнообразных задач и доказательства математических теорем.
Основные правила для считывания и вычисления суммы включают в себя использование знака суммы ∑ и указание верхнего и нижнего пределов суммирования. Верхний предел обозначает последний индекс в сумме, а нижний предел — первый индекс. Сумма может содержать переменную, которая меняется от нижнего до верхнего предела, а также выражение, которое зависит от этой переменной.
Например, сумма чисел от 1 до 10 может быть записана как ∑i=110 i. Здесь переменная i меняется от 1 до 10, а выражение i просто равно текущему значению переменной. При вычислении этой суммы получается результат 55.
Правильное использование скобок, индексов и символа суммы позволяет четко определить, какие элементы нужно сложить и какие пропустить. Кроме того, суммы могут иметь различные свойства, такие как ассоциативность и дистрибутивность, которые позволяют применять различные техники и методы для их вычисления.
В данной статье мы рассмотрим основные правила для суммирования, приведем примеры различных видов сумм и дадим рекомендации по правильному подсчету сумм в высшей математике. Понимание этих правил и методов поможет вам уверенно работать с суммами и применять их в своих исследованиях и задачах.
Высшая математика: необходимость правильного подсчета суммы
Основные правила подсчета сумм в высшей математике включают в себя:
- Линейность: сумма двух или более слагаемых равна сумме каждого слагаемого по отдельности. То есть, сумма a + b + c равна сумме a, b и c.
- Перестановочная: порядок слагаемых не влияет на сумму. То есть, сумма a + b равна сумме b + a.
- Ассоциативность: при сложении трех или более слагаемых, результат не зависит от того, какие из них сложены сначала. То есть, сумма (a + b) + c равна сумме a + (b + c).
Применение этих правил помогает систематизировать и упрощать подсчет сумм в сложных формулах. Например, при решении задач по теории вероятностей или при вычислении интегралов.
Важно также уметь правильно применять данные правила к специальным типам сумм, таким как геометрические прогрессии или биномиальные коэффициенты. Умение правильно считать суммы в высшей математике является ключевым навыком для прогрессирования в данной науке и успешного решения различных задач.
Основные правила счета в высшей математике

В высшей математике существует ряд основных правил счета, которые нужно знать и уметь применять. Они помогут вам правильно считать суммы и оперировать числами в сложных математических выражениях.
Вот основные правила счета в высшей математике:
- Правило сложения: сумма двух чисел равна их алгебраической сумме. Например, 2 + 3 = 5.
- Правило вычитания: разность двух чисел равна их алгебраической разности. Например, 5 — 3 = 2.
- Правило умножения: произведение двух чисел равно их алгебраическому произведению. Например, 2 * 3 = 6.
- Правило деления: частное двух чисел равно их алгебраическому частному. Например, 6 / 3 = 2.
- Правило возведения в степень: число, возведенное в степень, равно произведению этого числа на себя столько раз, сколько указано в степени. Например, 2^3 = 2 * 2 * 2 = 8.
- Правило извлечения корня: корень из числа равен числу, которое возводится в квадрат и дает это число. Например, √9 = 3.
Это основные правила счета, с которыми вы должны быть знакомы в высшей математике. Они являются фундаментом для дальнейших математических операций и позволяют решать сложные задачи и уравнения. Освоив эти правила, вы сможете более уверенно и точно выполнять вычисления в своих математических исследованиях и задачах.
Сложение и вычитание: основные операции
Сложение выполняется путем объединения двух или более чисел в одно число, называемое суммой. При сложении чисел, каждое число называется слагаемым, а результат — суммой.
Вычитание, напротив, выполняется для нахождения разности между двумя числами. Одно число называется уменьшаемым, а другое — вычитаемым. Результат вычитания называется разностью.
Для выполнения сложения и вычитания, можно использовать таблицу:
ОперацияПримерРезультат
| Сложение | 5 + 7 | 12 |
| Вычитание | 10 — 3 | 7 |
Применение правил сложения и вычитания позволяет точно вычислить сумму и разность чисел в высшей математике.
Умножение и деление: правила и примеры
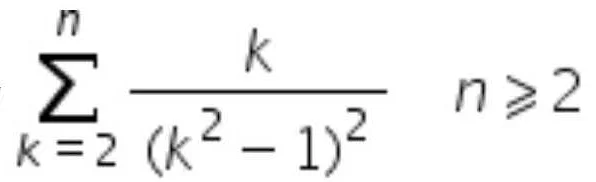
Правила умножения:
- Умножение двух чисел производится путем перемножения их значений.
- Умножение числа на ноль всегда равно нулю.
- Умножение числа на единицу оставляет число без изменений.
- Умножение числа на отрицательное число меняет знак результата на противоположный.
- Умножение числа на десятичную дробь выполняется путем перемножения числа на числитель дроби, а затем деления результата на знаменатель.
Примеры умножения:
2 * 3 = 6
5 * 0 = 0
7 * 1 = 7
-4 * 2 = -8
3 * (1/2) = 1.5
Правила деления:
- Деление одного числа на другое производится путем умножения делимого на обратное число делителя.
- Деление числа на ноль является невозможным.
- Деление числа на единицу оставляет число без изменений.
- Деление числа на отрицательное число меняет знак результата на противоположный.
- Деление числа на десятичную дробь выполняется путем умножения числа на знаменатель дроби, а затем деления результата на числитель.
Примеры деления:
10 / 2 = 5
8 / 4 = 2
12 / 1 = 12
-15 / 3 = -5
4 / (1/2) = 8
Суммирование бесконечных рядов: приемы и методы
Один из основных методов суммирования бесконечных рядов — метод частичных сумм. Этот метод заключается в вычислении суммы первых n членов ряда и последующем устремлении n к бесконечности. Если последовательность частичных сумм сходится к некоторому числу, то это число считается суммой бесконечного ряда.
Еще одним методом суммирования бесконечных рядов является метод замены переменной. Этот метод заключается в замене переменной в исходном ряде таким образом, чтобы получить новый ряд, сумму которого можно вычислить. Затем, после вычисления суммы нового ряда, производится обратная замена переменной, чтобы получить сумму исходного ряда.
Другим методом суммирования бесконечных рядов является метод интегрирования. Он основан на связи между бесконечными рядами и определенными интегралами. С помощью этого метода можно перейти от суммы ряда к интегралу и наоборот, что упрощает вычисление суммы бесконечного ряда.
При суммировании бесконечных рядов необходимо учитывать различные признаки сходимости и расходимости рядов, такие как признак сравнения, признак Даламбера, признак Коши и др. Эти признаки позволяют определить, сходится ли ряд или расходится, и, в случае сходимости, вычислить его сумму.
Суммирование бесконечных рядов является важным инструментом в высшей математике и находит применение в различных областях, включая анализ, математическую физику, теорию вероятностей и др. Правильное применение приемов и методов суммирования бесконечных рядов позволяет решать сложные математические задачи и получать точные результаты.
Интегрирование: основные приемы
Основными приемами интегрирования являются:
- подстановка;
- интегрирование по частям;
- разложение на простейшие дроби;
- использование тригонометрических тождеств;
- замена переменной;
- интегрирование рациональной функции.
Каждый из этих приемов имеет свои особенности и применяется в зависимости от сложности функции и условий задачи.
Прием подстановки позволяет осуществить замену переменной, которая упрощает интегрирование. Интегрирование по частям позволяет свести интеграл от произведения двух функций к интегралу от одной функции и её производной. Разложение на простейшие дроби применяется для интегрирования рациональных функций. Использование тригонометрических тождеств позволяет свести сложные тригонометрические функции к более простым. Замена переменной позволяет изменить форму интеграла для более удобного интегрирования. И, наконец, интегрирование рациональной функции – это процесс нахождения интеграла от дробной функции.
Использование этих приемов требует практики и опыта. Чем больше задач решено, тем легче становится интегрирование. Важно также знать основные свойства интеграла и уметь применять их в задачах.
Примеры высшей математики
Высшая математика включает в себя множество различных математических концепций и методов, которые применяются для решения сложных проблем и задач. Ниже приведены несколько примеров высшей математики:
ПримерОписание
| Интегрирование функций | Интегрирование является процессом нахождения площади под кривой, заданной функцией. Этот метод часто используется для нахождения площади фигур, объемов тел и других физических величин. |
| Дифференцирование функций | Дифференцирование является процессом нахождения производной функции, то есть ее скорости изменения. Этот метод используется для определения экстремумов функций и изучения их поведения. |
| Теория вероятностей | Теория вероятностей изучает случайные события и определяет вероятности их возникновения. Эта область математики часто используется в финансовой аналитике, статистике и других областях, связанных с анализом данных. |
| Линейная алгебра | Линейная алгебра изучает линейные уравнения и операции с векторами и матрицами. Она широко применяется в физике, компьютерной графике, экономике и других областях, связанных с моделированием и анализом данных. |
| Теория множеств | Теория множеств изучает свойства и отношения между элементами множеств. Она является основой для многих других областей математики, включая теорию групп, топологию и математическую логику. |
Это только небольшая часть того, что включает в себя высшая математика. Она имеет широкий спектр применений и играет важную роль в различных областях науки и техники.
Подсчет суммы геометрической прогрессии
Формула для подсчета суммы геометрической прогрессии выглядит следующим образом:
S = a * (rn — 1) / (r — 1)
Где:
- S – сумма геометрической прогрессии;
- a – первый элемент прогрессии;
- r – знаменатель прогрессии;
- n – количество элементов прогрессии.
Используя данную формулу, можно легко и быстро вычислить сумму геометрической прогрессии без необходимости перебирать все элементы. Это существенно упрощает подсчет и позволяет сэкономить время и усилия.
Пример:
Рассмотрим геометрическую прогрессию с первым элементом a = 2, знаменателем r = 3 и количеством элементов n = 4. Чтобы найти сумму этой прогрессии, подставим значения в формулу:
S = 2 * (34 — 1) / (3 — 1)
S = 2 * (81 — 1) / 2
S = 2 * 80 / 2
S = 80
Таким образом, сумма геометрической прогрессии с первым элементом 2, знаменателем 3 и количеством элементов 4 равна 80.
Расчет интеграла от функции

Расчет интеграла от функции производится с использованием специального символа ∫ (знака интеграла). Сам интеграл записывается в виде ∫f(x)dx, где f(x) – подынтегральная функция, а dx означает малый приращение аргумента x.
Для расчета интеграла от функции следует применить соответствующие методы интегрирования. Существует множество методов, включая методы аналитического интегрирования, численные методы и методы приближенного интегрирования.
Аналитическое интегрирование позволяет находить аналитическое выражение для интеграла от заданной функции. В этом случае происходит поиск первообразной (антипроизводной) функции f(x), то есть функции F(x), производная которой равна исходной функции, f'(x) = f(x). Затем интеграл от функции f(x) вычисляется как F(b) — F(a), где [a, b] – интервал интегрирования.
Численные методы интегрирования используются для нахождения численного значения интеграла, когда аналитическое выражение для него найти сложно или невозможно. Наиболее распространенными численными методами являются метод прямоугольников, метод тrapezoid, метод Симпсона и другие.
Методы приближенного интегрирования, включая численные методы, позволяют оценить значение интеграла с заданной точностью. Они основаны на разбиении интервала интегрирования на части и вычислении интеграла для каждой части с последующим сложением результатов.
Таким образом, расчет интеграла от функции является важной задачей в математическом анализе и имеет множество практических применений, включая физику, экономику, статистику и другие области науки и техники.
Суммирование ряда Фибоначчи
- 0
- 1
- 1
- 2
- 3
- 5
- 8
- 13
- 21
- 34
- и так далее…
Для суммирования ряда Фибоначчи можно использовать различные методы. Один из них — метод математической формулы. Для этого существует формула Бине, которая позволяет вычислить n-ый элемент ряда Фибоначчи:
F(n) = ((1 + √5)/2)^n — ((1 — √5)/2)^n / √5
Однако данная формула может быть сложной для понимания и применения. Вместо этого можно воспользоваться рекурсией или циклом для вычисления суммы ряда Фибоначчи.
Например, следующий код на языке Python позволяет вычислить сумму первых n элементов ряда Фибоначчи:
«`python
def fibonacci_sum(n):
fib = [0, 1] # начальные значения ряда Фибоначчи
for i in range(2, n+1):
fib.append(fib[i-1] + fib[i-2]) # добавление нового элемента в ряд
return sum(fib[:n]) # суммирование первых n элементов
n = 10 # количество элементов для суммирования
print(fibonacci_sum(n)) # вывод суммы
В данном примере мы используем цикл для генерации ряда Фибоначчи и функцию `sum()` для получения суммы первых n элементов. Этот код выведет сумму первых 10 элементов ряда Фибоначчи.
Таким образом, суммирование ряда Фибоначчи может быть выполнено с использованием различных методов, включая математические формулы, рекурсию и циклы. Выбор конкретного метода зависит от требуемой точности и эффективности вычислений.
Видео по теме:
Как правильно складывать числа в высшей математике?
В высшей математике сложение чисел выполняется путем поэлементного сложения разрядов. Например, если у вас есть два числа, 123 и 456, то для их сложения нужно сложить соответствующие разряды: 3+6=9, 2+5=7 и 1+4=5. Полученные значения записываются в виде суммы: 579.
Можете привести пример сложения в высшей математике?
Конечно! Рассмотрим сложение двух многочленов: (2x^2 + 3x + 5) + (x^2 — 2x + 1). Для сложения многочленов нужно сложить соответствующие степени переменной. В данном случае, мы получим: (2x^2 + x^2) + (3x — 2x) + (5 + 1) = 3x^2 + x + 6.

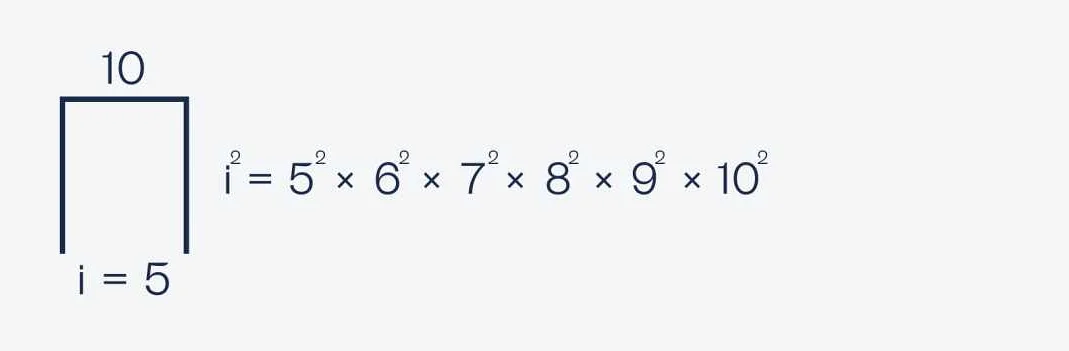



Эта статья очень полезна для всех, кому интересна высшая математика. Я всегда задавался вопросом, как правильно считать сложные суммы и эта статья дала мне ответы. Она осветила основные правила и привела примеры, которые помогли мне лучше понять и запомнить материал. Теперь я знаю, что сумму можно считать пошагово, разбивая ее на простые слагаемые и применяя соответствующие формулы. Это позволяет избежать ошибок и получить точный результат. Примеры, представленные в статье, помогли мне усвоить эти правила на практике. Теперь я гораздо увереннее в своих математических навыках и спокойно справляюсь с сложными суммами. Большое спасибо автору за такую полезную и понятную статью!
Статья очень полезна для всех, кто учится высшей математике. Я всегда задавался вопросом о том, как правильно считать сумму, особенно когда речь идет о бесконечных рядах. Этот материал помог мне разобраться в основных правилах и принципах. Конечно, я уже знал о закономерностях суммы арифметической прогрессии, но теперь я осознал, что могу применять эти знания и в других случаях. Очень полезными оказались примеры, которые помогли мне лучше усвоить материал. Статья очень доступно написана, и даже сложные темы объяснены понятно. Большое спасибо автору за такой полезный материал!
Статья действительно очень полезная и понятная для тех, кто углубленно изучает математику. Она помогла мне лучше разобраться в том, как правильно считать суммы в высшей математике. Основные правила, о которых здесь рассказывается, помогли мне улучшить свои навыки и уверенность в решении сложных задач. Особенно понравились примеры, которые четко и наглядно демонстрируют применение правил. Большое спасибо автору за такую подробную и понятную статью! Теперь я чувствую себя гораздо увереннее в своих счетных навыках в высшей математике.
Отличная статья! Я давно хотел разобраться с этим вопросом. Считать сумму в высшей математике всегда казалось мне сложным. Но благодаря вашим основным правилам и примерам, все стало намного понятнее. Теперь я знаю, что нужно уметь распознавать вид суммы и правильно применять соответствующие формулы. Я осознал, что важно быть внимательным и аккуратным, чтобы не допустить ошибки. Теперь я готов практиковаться и применять эти правила на практике. Спасибо вам за такую подробную и понятную статью!