Математика как перевести обычную дробь в десятичную

Узнайте, как перевести обычную дробь в десятичную форму с помощью математики. Шаг за шагом объясняется процесс преобразования и предоставляются примеры для лучшего понимания.

В математике обычная дробь представляет собой дробное число с числителем и знаменателем. Обычные дроби можно превратить в десятичные дроби, чтобы получить численное значение. Это полезно, когда нужно выполнить дальнейшие математические операции или сравнить дробные числа.

Для превращения обычной дроби в десятичную дробь существует несколько способов, но в данной статье мы рассмотрим математический подход. Он основан на преобразовании знаменателя дроби в степень числа 10. Таким образом, мы сможем получить десятичное представление данной дроби.

Например, рассмотрим обычную дробь 3/4. Чтобы превратить ее в десятичную дробь, мы заменяем знаменатель 4 на 10 в степени 1, получая 40. Затем делим числитель 3 на полученный знаменатель 40 и получаем десятичное представление дроби — 0.75.

Таким образом, математический подход позволяет нам превратить обычную дробь в десятичную дробь, используя простые математические операции. Этот метод особенно полезен при работе с дробными числами в математических расчетах или анализе данных.

Важно: при превращении обычной дроби в десятичную дробь необходимо быть внимательным, чтобы избежать ошибок в вычислениях. Также следует помнить, что некоторые обычные дроби имеют бесконечные или периодические десятичные представления.

Методы преобразования обычной дроби в десятичную дробь

1. Деление с остатком:

Один из самых простых способов преобразования обычной дроби в десятичную дробь — это деление с остатком. Для этого требуется разделить числитель дроби на знаменатель и записать получившееся частное в виде десятичной дроби. Если остаток от деления не равен нулю, следует продолжить деление, добавив нули к остатку и повторив процесс.

2. Десятичная дробь в виде суммы дробей:

Второй метод заключается в представлении десятичной дроби в виде суммы дробей, где каждая дробь имеет знаменатель, являющийся степенью числа 10. Для этого требуется разделить числитель дроби на знаменатель и записать полученное частное в виде десятичной дроби. Затем следует продолжить деление, добавляя нули к остаткам и записывая полученные дроби в виде суммы.

3. Запись обыкновенной дроби в виде периодической десятичной:

Если после выполнения деления с остатком или представления десятичной дроби в виде суммы дробей получается периодическое число, то его можно записать в виде периодической десятичной дроби. Для этого следует обозначить повторяющуюся часть числа и записать ее после запятой, заключив в круглые скобки.

Выбор метода преобразования обычной дроби в десятичную дробь зависит от конкретной задачи и предпочтений решающего.

Видео по теме:

Математический подход к превращению обычной дроби в десятичную

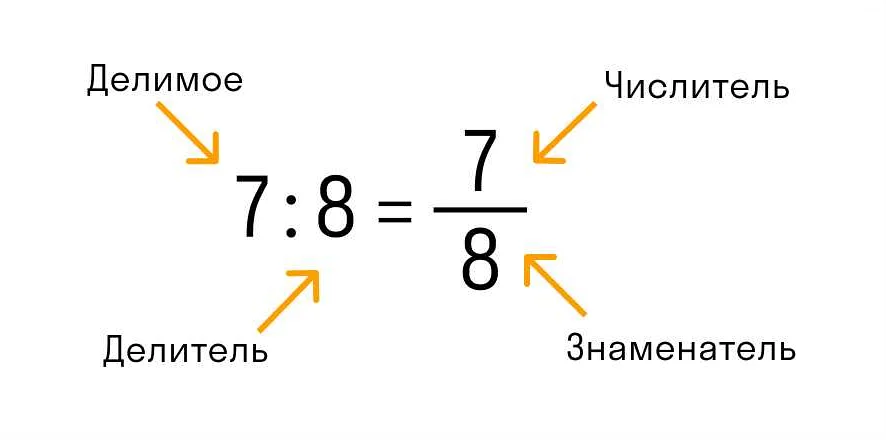
Математический подход основан на делении числителя дроби на знаменатель, что позволяет получить десятичную дробь. Чтобы выполнить это деление, необходимо разделить числитель на знаменатель и записать результат в виде десятичной дроби.

При выполнении деления обычной дроби на знаменатель, могут возникнуть две ситуации:

1. Деление является точным. В этом случае результатом деления будет конечная десятичная дробь, например, 0.25.
2. Деление является бесконечным. В этом случае результатом деления будет бесконечная десятичная дробь, которая может быть записана в виде периодической десятичной дроби, например, 0.3333…

Математический подход к превращению обычной дроби в десятичную позволяет получить точный или приближенный результат в зависимости от исходных данных. Он широко используется в различных областях науки, техники и финансов, где точность вычислений имеет особое значение.

Принцип работы расширенного деления

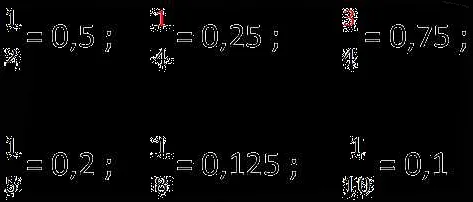
Принцип работы расширенного деления следующий:

1. Записываем делимое и делитель, а также приводим их к десятичным дробям, если они не являются таковыми.
2. Ставим делимое в числитель дроби и делитель в знаменатель.
3. Разделим числитель на знаменатель и запишем результат, дополнив его нулями после запятой.
4. Если полученная десятичная дробь не имеет периода и имеет ограниченное количество знаков после запятой, то деление заканчивается.
5. Если десятичная дробь получилась периодической, то продолжаем делить, добавляя нули после запятой.
6. Записываем остаток от деления после каждой итерации и сравниваем его с остатками, которые уже были.
7. Когда остаток повторяется, значит, период начинается. Период записывается в виде скобок после дроби, в которой цифры начинают повторяться.

Таким образом, принцип работы расширенного деления позволяет получить десятичную запись дроби и определить ее периодическую или не периодическую природу.

Как записать обычную дробь для превращения в десятичную

Обычная дробь состоит из числителя и знаменателя, которые записываются в виде дроби. Числитель указывается над знаменателем, разделяя их горизонтальной чертой. Например, дробь 3/4 состоит из числителя 3 и знаменателя 4, и записывается как 3/4.

Для превращения обычной дроби в десятичную форму, необходимо выполнить деление числителя на знаменатель. Например, чтобы превратить дробь 3/4 в десятичную форму, нужно разделить числитель 3 на знаменатель 4: 3 ÷ 4 = 0.75.

При записи обычной дроби для превращения в десятичную форму, важно следовать определенным правилам. Десятичная дробь должна быть записана с помощью точки, а не запятой. Например, дробь 1/2 должна быть записана как 0.5, а не 0,5.

Обычная дробьДесятичная форма

1/2	0.5
3/4	0.75
2/5	0.4

Таким образом, для превращения обычной дроби в десятичную форму, необходимо записать дробь в правильном формате и выполнить деление числителя на знаменатель. Полученный результат будет десятичным представлением обычной дроби.

Пример превращения обычной дроби в десятичную с помощью расширенного деления

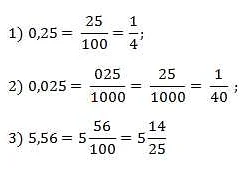
Превратим дробь 3/4 в десятичную дробь.

Шаг 1: Расставляем нули после запятой в делимом и ставим запятую в ответе.

0. , 75

Шаг 2: Делим 3 на 4. 3 не делится на 4, поэтому дописываем ноль после запятой и идем к следующей цифре.

0.0 , 75

Шаг 3: Делим 30 на 4. 30 делится на 4, получаем 7. Оставшееся число 2 записываем вместе с запятой в ответе.

0.07 , 5

Шаг 4: Делим 20 на 4. 20 делится на 4, получаем 5. Оставшееся число 0 записываем в ответе.

0.075 , 0

Шаг 5: Делим 0 на 4. 0 не делится на 4, поэтому дописываем ноль после запятой и заканчиваем деление.

0.0750

Таким образом, дробь 3/4 превращается в десятичную дробь 0.0750.

Как упростить превращение обычной дроби в десятичную с помощью округления

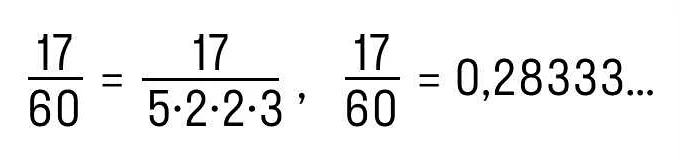
Превращение обычной дроби в десятичную может быть сложной задачей, особенно если дробь имеет большое количество десятичных разрядов. Однако существует способ упростить этот процесс с помощью округления.

Округление — это процесс приближения числа к ближайшему значению с заданным числом десятичных разрядов. В случае превращения обычной дроби в десятичную, округление может использоваться для упрощения полученного результата.

Для начала, необходимо выполнить деление числителя дроби на знаменатель. Затем полученное частное можно округлить с помощью определенного правила округления:

• При округлении до целого числа, десятичная часть отбрасывается.
• При округлении до определенного числа десятичных разрядов, последний разряд определяет тип округления: если он меньше 5, число округляется вниз, если он больше или равен 5, число округляется вверх.

Пример:

Рассмотрим дробь 3/4. Выполняем деление 3 ÷ 4 = 0.75. С помощью округления до двух десятичных разрядов, результат будет 0.75, так как последний разряд 5 меньше 5. Полученная десятичная дробь 0.75 является упрощенным результатом превращения обычной дроби в десятичную с помощью округления.

Использование округления существенно упрощает процесс превращения обычной дроби в десятичную. Однако важно помнить, что округление может привести к потере точности и увеличению погрешности. Поэтому, в зависимости от конкретной задачи, необходимо принять во внимание эти факторы и применять округление с умом.

Использование десятичных дробей в реальной жизни

Одной из наиболее распространенных областей, где мы сталкиваемся с десятичными дробями, является финансовая сфера. Ведение бухгалтерии, расчеты налогов, составление бюджета и управление финансами требуют понимания и работы с десятичными дробями. Когда мы рассчитываем проценты, суммы, налоги или другие финансовые показатели, мы часто используем десятичные дроби.

Десятичные дроби также широко используются в науке и технике. Например, при измерении физических величин, таких как длина, масса, объем или время, мы часто сталкиваемся с десятичными дробями. Они помогают нам точно измерять и описывать различные параметры и свойства объектов и явлений.

В торговле и коммерции десятичные дроби необходимы для точного расчета цен, скидок, налогов и долей. Они помогают нам определить стоимость товаров, рассчитать суммы платежей и оценить различные экономические показатели.

Наконец, десятичные дроби играют важную роль в повседневной жизни каждого из нас. Мы используем их, чтобы оценить вероятность событий, рассчитывать проценты скидок, делать покупки и многое другое. Понимание и умение работать с десятичными дробями является необходимым навыком, который помогает нам принимать рациональные решения и лучше разбираться в различных ситуациях.

Таким образом, десятичные дроби являются неотъемлемой частью нашей жизни. Они используются во многих сферах и областях, помогая нам решать различные задачи и делать более точные расчеты. Понимание и умение работать с десятичными дробями позволяют нам лучше понимать и оценивать мир вокруг нас.

Вопрос-ответ:

Как превратить обычную дробь в десятичную?

Чтобы превратить обычную дробь в десятичную, нужно разделить числитель на знаменатель. Например, если у нас есть дробь 3/4, мы должны разделить 3 на 4, что даст нам результат 0.75.

Каким образом можно преобразовать дробь в десятичную дробь?

Существует несколько способов преобразовать дробь в десятичную дробь. Один из них — деление числителя на знаменатель. Другой способ — выразить дробь в виде суммы десятичной дроби и целого числа. Например, дробь 5/2 можно представить как 2.5, что равно 2 + 0.5.

Можно ли превратить любую обычную дробь в десятичную?

В большинстве случаев можно превратить обычную дробь в десятичную. Однако некоторые дроби могут иметь бесконечное число десятичных знаков или периодическую последовательность цифр. В таких случаях результат будет представлен округленным числом или десятичной дробью с периодической последовательностью.

Как преобразовать дробь с периодической последовательностью в десятичную?

Для преобразования дроби с периодической последовательностью в десятичную нужно записать уравнение, где x — сама дробь, и решить его. Например, если у нас есть дробь 1/3 с периодом 3, мы можем записать уравнение x = 0.333… и умножить его на 10, чтобы избавиться от периода. После этого вычесть из уравнения исходную дробь, чтобы получить новое уравнение 10x — x = 3. После решения уравнения получим x = 1/3 = 0.333…).