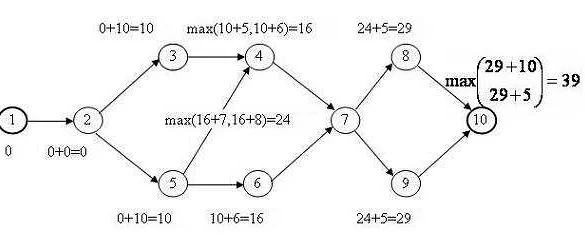
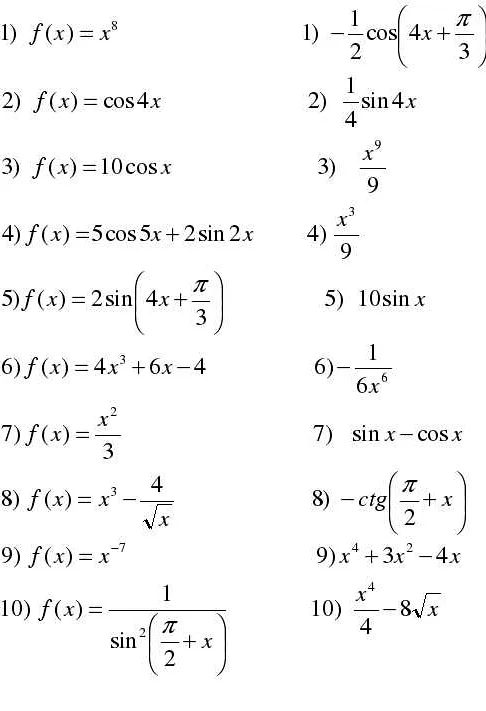Как решать интегралы: подробное руководство по высшей математике

Узнайте как решать интегралы высшей математики, методы и секреты выполнения сложных задач на примерах с подробными объяснениями. Облегчите свою жизнь во время учебы математике с нашей помощью!

Интегралы — это один из ключевых элементов высшей математики, который используется для нахождения площадей, объёмов, скоростей и других важных параметров. Но, как и любой другой раздел математики, интегралы могут быть сложными и запутанными. В этой статье мы рассмотрим основы интегралов и покажем, как их можно решать.

Для начала, нам нужно понимать, что такое интеграл. В кратце, интеграл является обратной операцией производной — он позволяет найти функцию, которая была проинтегрирована. Простым языком, интеграл — это способ нахождения площади под графиком функции.

Чтобы решать интегралы, нужно знать некоторые основные методы интегрирования. В статье мы рассмотрим несколько из них, включая метод интегрирования по частям, метод замены переменной и метод интегрирования рациональной функции.

Что такое интегралы?

Интегралы — это важный математический инструмент, который позволяет решать множество задач в физике, инженерии, экономике и других областях. Они служат для нахождения площадей, объёмов, массы, центра масс, момента инерции и других характеристик объектов и явлений.

Интеграл — это математический объект, определяемый как предел суммы значений функции на каждом элементарном отрезке разбиения при условии, что ширина отрезков стремится к нулю. Это позволяет вычислять значение функций, которые изменяются от момента к моменту, а также площади под кривой графика.

Одними из самых известных интегралов являются определённые интегралы, которые используются для вычисления площади фигуры, ограниченной кривой и осями координат. Также существуют интегралы Ньютона-Лейбница, которые позволяют находить функцию по её производной.

Интегралы являются важным инструментом в математическом анализе и используются для решения большого количества задач, связанных с вычислением площадей, объёмов, массы, центра масс, момента инерции и других характеристик объектов и явлений.

Основная задача математического анализа — это нахождение интегралов, которые позволяют определить значения функций в различных точках. Интегралы играют важную роль в решении задач различных отраслей науки и техники.

Видео по теме:

Как решать интегралы методом интегрирования?

Метод интегрирования основан на обратном действии дифференцирования функций. Интеграл может быть решен, если известна производная функции. Если же функция не может быть дифференцирована аналитически, то к её интегрированию приходят эвристические методы.

Первый и основной метод интегрирования – это метод прямого интегрирования. Он заключается в том, что нужно разбить интегрируемую функцию на маленькие части и затем сложить полученные значения. Для этого используются различные формулы, например, формула прямоугольников, трапеций, Симпсона.

Ещё одним методом интегрирования является метод замены переменной. Он заключается в замене переменной интегрирования на новую переменную, чтобы получившийся интеграл стал более простым. Для этого нужно провести несколько алгебраических преобразований.

Также существует метод интегрирования по частям. Он основывается на формуле дифференцирования произведения функций. Она позволяет свести интеграл от произведения двух функции к интегралу от одной из них и от произведения её производной на вторую функцию.

Ещё одним методом интегрирования является метод интегрирования неопределённых коэффициентов. Он заключается в том, чтобы найти функцию, задав которую потребуется только задать некоторые неизвестные коэффициенты. Коэффициенты определяются из начальных или граничных условий, которые задаются с помощью самой задачи.

Выбор метода интегрирования зависит от сложности интегрируемой функции и от особенностей задачи. В любом случае, интегрирование – очень важный процесс в математике, который позволяет решать многие физические и технические задачи.

Сложные интегралы: как их решать?

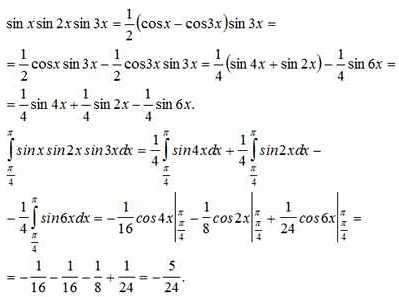
При решении сложных интегралов необходимо использовать различные методы, которые позволяют привести выражение к более простому виду. Одним из таких методов является замена переменной. Если в интеграле присутствуют функции, содержащие степенные и тригонометрические функции, то полезно воспользоваться формулами приведения.

Другим эффективным методом является интегрирование по частям. Оно позволяет разделить сложный интеграл на два более простых. В этом случае одна из двух функций f(x) или g'(x) выбирается в качестве дифференциала, а вторая функция интегрируется.

Также можно использовать метод Римана, который заключается в разбиении области интегрирования на множество частей, описываемых функцией, а затем оценивании интеграла на каждой из этих частей. После этого значения интегралов на каждой из частей складываются.

• Интегрирование по частям
• Замена переменной
• Метод Римана

Однако стоит помнить, что интегрирование — это не только математическая операция, но и наука, которая требует определенного опыта и навыков. Поэтому при работе с интегралами нужно быть терпеливым, внимательным и не бояться экспериментировать.

Вопрос-ответ:

Как быстро найти первообразную функции?

Для быстрого нахождения первообразной функции следует использовать формулы интегрирования и методы интегрирования, а также приемы замен переменных, интегрирования по частям и тригонометрические подстановки.

Что такое неопределенный интеграл?

Неопределенный интеграл — это обратная операция к дифференцированию, и он позволяет найти первообразную функции. Неопределенный интеграл обозначается символом ∫f(x)dx, где f(x) — подынтегральная функция, а dx — дифференциал переменной, по которой производится интегрирование.

Какие методы интегрирования бывают?

Существует множество методов интегрирования, таких как интегрирование по частям, замена переменных, требующая замены на этих функциях или элементарных функциях большей степени сложности, тригонометрические подстановки, метод Эйлера, метод Лапласа, метод Монте-Карло и др.

Что такое замена переменных в интеграле?

Замена переменных — это метод преобразования интеграла путем замены переменной на новую величину, которая входит в подынтегральную функцию. В результате интеграл с трудной подынтегральной функцией превращается в интеграл с более простой функцией. Для замены переменных нужно знать формулы замены и иметь понимание, как выбирать соответствующие переменные и границы интегрирования.

Как осуществить интегрирование по частям?

Интегрирование по частям — это метод интегрирования, который позволяет интегрировать произведение двух функций. Для применения этого метода нужно знать формулу интегрирования по частям — ∫u dv = uv — ∫v du, где u и v — выбранные функции. При применении этого метода нужно выбрать такие функции, чтобы их произведение было проще интегрирования, чем отдельно взятые функции.

Какие ограничения бывают на выбор функции для требующей замены переменных?

При замене переменных в интеграле нужно учитывать ограничения на выбор функции, чтобы не получилась некорректная замена. Функция должна быть однозначной и дифференцируемой на интервале интегрирования, и она должна принимать значения от 0 до бесконечности. Также нужно учитывать, что заменяемая переменная должна быть независимой от остальных переменных в интеграле и принимать значения на всем интервале интегрирования.

Какие тригонометрические подстановки бывают?

Для решения сложных интегралов можно использовать тригонометрические подстановки, которые заменяют подынтегральную функцию на тригонометрическую функцию и устанавливают соответствующие границы интегрирования. Такие подстановки могут быть простыми, например, k tan x, k sec x или k csc x, или сложными, например, k tan x / (a + b sin x) или k cot x / (a + b cos x).

Примеры решения интегралов: шаг за шагом

Решение интегралов — одна из основных задач математического анализа. В этом процессе необходимо использовать знания, полученные в ходе изучения этих наук. Рассмотрим примеры решения интегралов, шаг за шагом.

Пример 1: Найдем неопределенный интеграл от функции f(x) = 2x + 3:

1. Записываем формулу для неопределенного интеграла: ∫f(x)dx
2. Заменяем функцию на данную в условии: ∫(2x + 3)dx
3. Выносим из интеграла константу: 2∫xdx + 3∫dx
4. Вычисляем интегралы: x^2 + 3x + C
5. Получаем ответ: ∫(2x + 3)dx = x^2 + 3x + C

Пример 2: Найдем определенный интеграл от функции g(x) = 7x^2 на отрезке [0, 3]:

1. Записываем формулу для определенного интеграла: ∫[a, b]g(x)dx
2. Заменяем функцию на данную в условии: ∫[0, 3]7x^2dx
3. Выносим из интеграла константу: 7∫[0, 3]x^2dx
4. Вычисляем интеграл: (7/3)x^3
5. Подставляем пределы интегрирования и получаем ответ: ∫[0, 3]7x^2dx = (7/3)27 — (7/3)0 = 63

Таким образом, для решения интегралов необходимо применять соответствующие формулы и полученные знания в ходе изучения математического анализа. Следуя шагам, приведенным в примерах выше, можно решить интегралы различной сложности.

Интегрирование по частям: что это такое и как применять?

Интегрирование по частям — это метод, который позволяет вычислить определенный или неопределенный интеграл произведения двух функций. В общем случае, если мы имеем произведение двух функций f(x)g(x), то мы можем применить формулу интегрирования по частям:

∫f(x)g(x)dx = f(x)∫g(x)dx — ∫f'(x)∫g(x)dx dx

где f'(x) — производная функции f(x).

Для того чтобы применить этот метод, нужно выбрать одну функцию в качестве u и ее производную в качестве du, а другую функцию в качестве dv и вычислить ее интеграл. После этого подставить полученные значения в формулу и вычислить интеграл.

Интегрирование по частям можно применять в различных случаях, например, при вычислении интегралов от тригонометрических функций, логарифмических функций, экспоненциальных функций и т.д.

Замена переменной в интеграле: техника и примеры применения

Одной из ключевых техник решения интегралов является замена переменной. Эта техника позволяет свести сложный интеграл к более простому виду и упростить его вычисление.

Для замены переменной в интеграле необходимо произвести замену одной переменной на другую в пределах интегрирования, а затем выразить новый интеграл через старый с помощью формулы замены переменной.

Примером замены переменной может служить замена $x=\sin u$ при решении интеграла $\int{\cos x} \,dx$. После замены переменной получим интеграл $\int{\cos x} \,dx = \int{\cos(\sin u)} \cos u\,du.$ Затем применяя формулу замены переменной, получаем новый интеграл $\int{\cos(\sin u)} \cos u\,du = \int{(\cos x)\sqrt{1-x^2}\,dx}.$

Другим примером может служить замена $x=e^t$ при вычислении интеграла $\int{\frac{1}{x\ln x}} \,dx.$ После замены переменной получим интеграл $\int{\frac{1}{x\ln x}} \,dx = \int{\frac{1}{t}\,dt}.$ Затем, используя формулу замены переменной, получаем новый интеграл $\int{\frac{1}{t}\,dt} = \ln|\ln x| + C.$

Таким образом, замена переменной в интеграле — это мощный инструмент при решении сложных интегралов. Она позволяет привести интеграл к более простому виду и значительно упростить вычисления.

Разложение на простые слагаемые в интегралах: метод и примеры

Разложение на простые слагаемые — это метод решения интегралов, в котором функция под интегралом представляется в виде суммы простых дробей.

Для того чтобы разложить функцию на простые слагаемые, ее необходимо сначала привести к общему знаменателю и разложить каждое слагаемое на простые дроби. Дроби затем собираются вместе и находятся коэффициенты при каждой из них.

Например, для интеграла ∫(2x+3)/(x^2+3x+2)dx можно сначала раскладывать знаменатель на простые множители: x^2+3x+2=(x+1)(x+2). Затем функцию можно представить в виде 2/(x+1)+1/(x+2), после чего интеграл становится проще решить.

Разложение на простые слагаемые часто используется в вычислениях обратных преобразований Лапласа и методах решения дифференциальных уравнений. Он является важным инструментом для математических вычислений и находит применение в различных областях науки и техники.

Некоторые типичные интегралы: как решать без расчетов?

Некоторые интегралы могут быть решены без необходимости проведения вычислений. Для этого необходимо знать некоторые особенности и свойства функций, которые входят в интеграл.

Например, интеграл ∫(1/x)dx может быть решен без расчетов, так как интеграл данной функции равен ln|x| + C, где C — произвольная постоянная. Также интеграл ∫(e^x)dx может быть решен без расчетов, так как интеграл данной функции равен e^x + C, где C — произвольная постоянная.

Кроме того, существует несколько типов интегралов, которые могут быть решены без необходимости проведения вычислений. Например, интегралы, содержащие четную функцию на интервале симметрии, могут быть решены без расчетов. Также интегралы, содержащие функции, обладающие периодическими свойствами, могут быть решены без расчетов.

Итак, если вы сталкиваетесь с интегралом, который вы не можете решить способом подсчета, попробуйте использовать эти хитрости и свойства функций, чтобы решить его без необходимости проведения вычислений.

Трюки и хитрости при решении интегралов

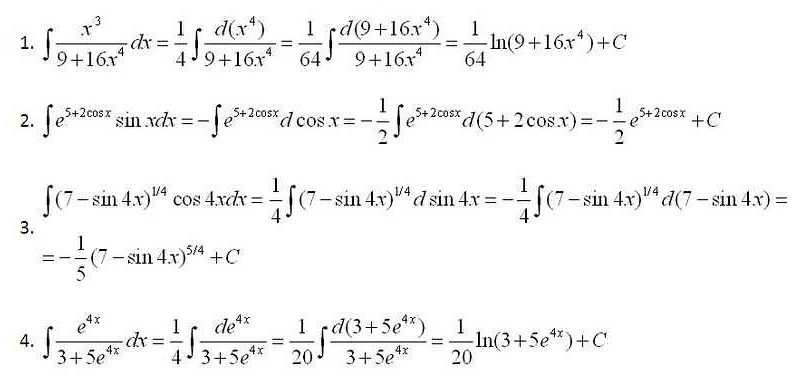
1. Преобразование интеграла:

Интеграл можно преобразовать, перейдя от одного вида к другому. Например, можно заменить переменную или разложить функцию в ряд Тейлора. Это позволит упростить задачу и решить интеграл с помощью элементарных функций.

2. Использование таблиц интегралов:

Таблицы интегралов – это специальные справочники, содержащие формулы для интегралов от различных функций. Их можно использовать, чтобы найти интеграл быстро и без необходимости выводить формулу изначально.

3. Разбиение интеграла на несколько частей:

Если интеграл сложный, то его можно разбить на несколько частей и решить каждую из них отдельно. Это позволит упростить вычисления и найти решение точнее.

4. Интегрирование по частям:

Интегрирование по частям – это метод, который позволяет свести сложный интеграл к более простому виду. Для этого необходимо разложить произведение двух функций на можно и применить формулу интегрирования по частям.

5. Нахождение общего решения:

Если нужно найти общее решение дифференциального уравнения, то можно использовать методы интегрирования, чтобы найти все возможные решения. Затем, объединив эти решения, можно получить общее решение задачи.

6. Проверка ответа:

Важно проверить полученный ответ, подставив его в исходный интеграл или дифференциальное уравнение. Это позволит убедиться в правильности решения и выявить ошибки в случае их наличия.

Практические задания по решению интегралов

Для того чтобы научиться решать интегралы, нужно не только уметь применять формулы для вычисления интегралов, но и уметь выбирать подходящую методику интегрирования. Поэтому мы предлагаем несколько практических заданий, которые помогут попрактиковаться в решении интегралов различной сложности.

Задание 1.

Вычислить интеграл:

∫ (3×2 + 4x — 1) dx

Для решения данного интеграла нужно использовать базовые правила интегрирования. Необходимо разложить интеграл на сумму интегралов каждого из слагаемых, затем применить формулы для вычисления интеграла от степенной функции и константы.

Задание 2.

Вычислить интеграл:

∫ (x2 + x — 3) ex dx

Для решения данного интеграла нужно использовать метод интегрирования по частям. Необходимо выбрать первую и вторую функции, произвести дифференцирование первой функции и интегрирование второй, затем произвести замену переменных и решить полученное уравнении относительно неизвестной интеграла.

Задание 3.

Вычислить интеграл:

∫ x sin(x) dx

Для решения данного интеграла нужно использовать метод интегрирования по частям. Необходимо выбрать первую и вторую функции, произвести интегрирование первой функции и дифференцирование второй, затем произвести замену переменных и решить полученное уравнении относительно неизвестной интеграла.

Задание 4.

Вычислить интеграл:

∫ 1/(x2 — 4) dx

Для решения данного интеграла нужно использовать метод замены переменных. Необходимо произвести замену переменных, чтобы получить интеграл от простой функции, затем применить формулы для вычисления интеграла от степенной функции и логарифма.

Выполняя эти задания, вы научитесь применять различные методы интегрирования и выбирать подходящую методику для решения интегралов различной сложности.

Как наладить понимание решения интегралов и закончить успехом

Решение интегралов — это важный инструмент в высшей математике. Однако, не все студенты справляются с ним на первый раз. Чтобы наладить понимание решения интегралов и закончить успехом, необходимо придерживаться несложных правил:

• Понимание концепции интеграла. Прежде чем приступать к решению интегралов, необходимо хорошо понимать, что такое интеграл и за что он отвечает. Признаками хорошего понимания интеграла являются умение объяснить его своими словами и рассмотреть примеры.
• Овладение необходимой математической терминологией. Решение интегралов связано с некоторыми специальными терминами, которые студентам иногда трудно запомнить. Важно уделить время изучению и запоминанию терминов. Это поможет упростить понимание материала и уберечь от ошибок.
• Практика решения интегралов. Как и с любой математической темой, решение интегралов требует практики. Стоит решать как легкие, так и сложные задачи, чтобы закрепить свои знания и научиться применять их в практике.
• Обратная связь и консультации. Если у студента возникают затруднения, важно не пропускать вопросы и обращаться за помощью к преподавателю или другим студентам. Решение интегралов — это коллективное дело, и в совместной работе можно найти множество полезных ресурсов и идей.

Следование этим правилам поможет студентам наладить свое понимание решения интегралов и достичь успеха в высшей математике. Не бойтесь задавать вопросы, изучайте терминологию, упражняйтесь в решении задач, и вы обязательно закончите эту тему успешно.