Что такое интеграл простыми словами в математике
Содержимое
- 1 Что такое интеграл простыми словами в математике
- 1.1 Интеграл: Определение и суть
- 1.2 Видео по теме:
- 1.3 Понятие и основные свойства
- 1.4 Примеры и наглядное представление
- 1.5 Методы вычисления интегралов
- 1.6 Определенный интеграл и его вычисление
- 1.7 Неопределенный интеграл и его связь с производной
- 1.8 Применение интегралов в математике и физике
- 1.9 Вычисление площадей и объемов
- 1.10 Определение центра масс
- 1.11 Решение дифференциальных уравнений
- 1.12 Вопрос-ответ:
- 1.12.0.1 Зачем нужен интеграл в математике?
- 1.12.0.2 Как можно объяснить понятие интеграла простыми словами?
- 1.12.0.3 Какие методы существуют для вычисления интегралов?
- 1.12.0.4 В каких областях науки и техники применяются интегралы?
- 1.12.0.5 Как можно объяснить понятие интеграла простыми словами?
- 1.12.0.6 В каких случаях используется интеграл в математике?
Интеграл – это математическое понятие, которое используется для нахождения площади под кривой или для вычисления накопленной суммы изменений величины. В данной статье мы расскажем, что такое интеграл и как его применяют в математике.
Интеграл – одно из основных понятий математического анализа, которое позволяет находить площади под кривыми, вычислять средние значения функций и решать множество задач. Интеграл является обратной операцией к дифференцированию, исследует функции на их изменение величины в зависимости от времени, расстояния, объема и других параметров.
Понятие интеграла можно объяснить как сумму бесконечно малых приращений функции, умноженных на соответствующие элементы ее аргумента. На практике интеграл позволяет решать задачи, связанные с вычислением площадей, объемов, массы, моментов инерции и других характеристик фигур и тел.
Применение интеграла в математике широко распространено. С его помощью можно находить площади различных фигур, вычислять сумму бесконечно малых значений функций, а также решать дифференциальные уравнения, описывающие законы физики, химии и других наук. Интеграл имеет множество приложений в различных областях науки и техники.
Интеграл: Определение и суть

Основной идеей интеграла является нахождение площади фигуры, ограниченной кривой и осью абсцисс. Для этого мы делим область на бесконечное количество очень маленьких прямоугольников, вычисляем площадь каждого из них и затем суммируем все получившиеся значения.
Интеграл обычно обозначается символом ∫ («интеграл») и может иметь разные пределы интегрирования, которые указывают границы области, в пределах которой мы ищем площадь.
Интеграл имеет множество применений в различных областях науки и техники. Он позволяет решать задачи, связанные с вычислением площадей, объемов, длин кривых, скорости изменения величин и многих других.
Интеграл — это важный инструмент, который позволяет анализировать, предсказывать и оптимизировать различные процессы и явления в природе и науке. Понимание его сути и принципов работы позволяет нам лучше понимать и описывать окружающий мир.
Видео по теме:
Понятие и основные свойства
Основные свойства интеграла:
- Аддитивность: интеграл от суммы двух функций равен сумме интегралов каждой из функций.
- Линейность: интеграл от линейной комбинации функций равен линейной комбинации интегралов от каждой из функций.
- Интеграл от постоянной функции равен произведению значения функции на длину интервала интегрирования.
- Интеграл от неотрицательной функции всегда неотрицателен.
- Интеграл от функции, ограниченной сверху и снизу, всегда существует.
Эти свойства интеграла позволяют упростить вычисления и решать сложные задачи, используя основные методы интегрирования.
Примеры и наглядное представление
Для лучшего понимания концепции интеграла, рассмотрим несколько примеров и наглядных представлений.
Пример 1:
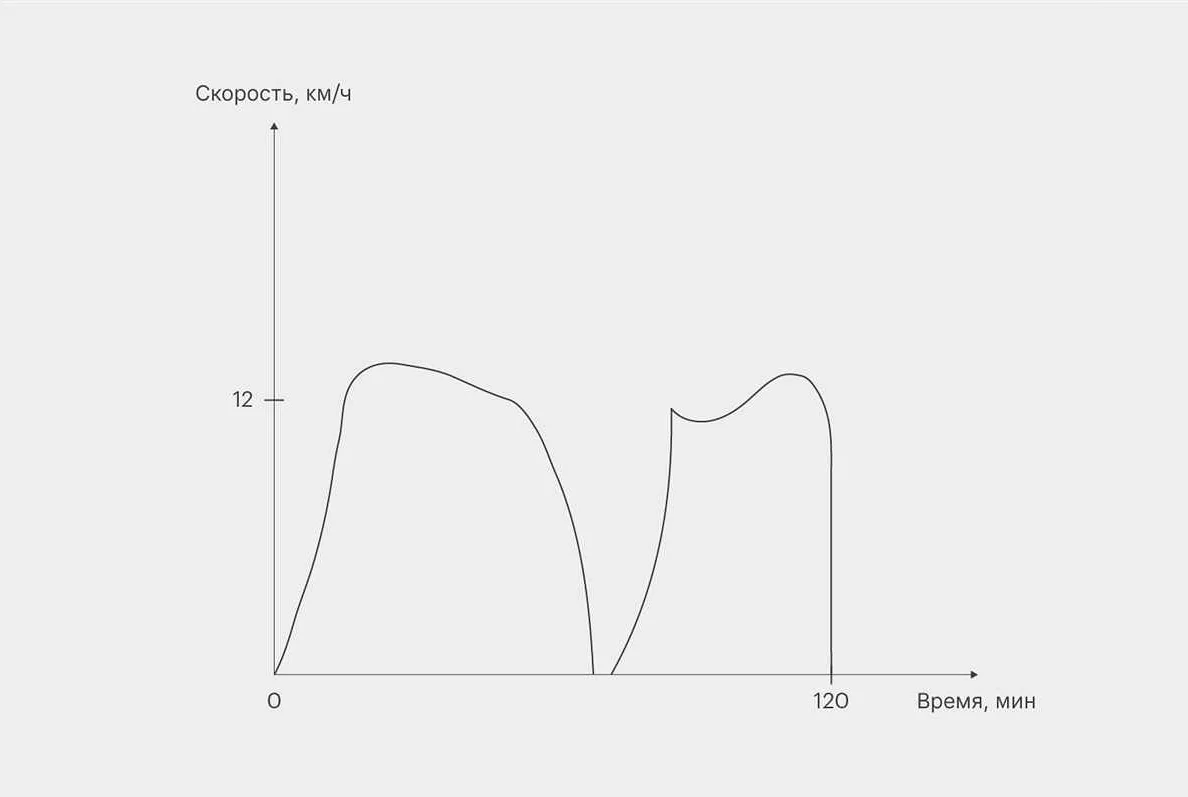
Предположим, у нас есть график функции, который представляет зависимость скорости тела от времени. Чтобы найти путь, пройденный телом за определенный промежуток времени, мы можем воспользоваться интегралом. Интеграл от функции скорости по времени даст нам значение пути.
Пример 2:
Представим, что у нас есть график функции, который показывает зависимость плотности населения от расстояния. Чтобы узнать, сколько людей проживает в определенной области, мы можем взять интеграл от этой функции на соответствующем интервале расстояний.
Наглядное представление:
Интеграл можно представить как площадь под кривой на графике функции. Разбивая эту площадь на бесконечно малые элементы и суммируя их, мы получаем значение интеграла. Это аналогия к тому, как можно представить сумму бесконечного числа маленьких прямоугольников, которые вместе образуют площадь под кривой.
Примеры и наглядное представление помогают нам увидеть, как интеграл может использоваться для нахождения различных значений и изучения свойств функций.
Методы вычисления интегралов
Одним из основных методов вычисления интегралов является метод прямоугольников. Он основан на разбиении области интегрирования на прямоугольники и вычислении суммы площадей этих прямоугольников. Чем мельче разбиение, тем точнее будет приближенное значение интеграла.
Еще одним методом вычисления интегралов является метод трапеций. Он основан на разбиении области интегрирования на трапеции и вычислении суммы площадей этих трапеций. Этот метод также дает приближенное значение интеграла, и его точность зависит от мелкости разбиения.
Также существуют методы численного интегрирования, такие как метод Симпсона. Он основан на аппроксимации подынтегральной функции квадратичной функцией и вычислении интеграла от этой аппроксимирующей функции. Метод Симпсона достаточно точен и может быть использован для вычисления интегралов различных функций.
Кроме того, существуют специальные техники вычисления интегралов, такие как интегрирование по частям или замена переменной. Они позволяют упростить интегрирование и найти точное значение интеграла для некоторых функций.
Все эти методы вычисления интегралов имеют свои преимущества и недостатки и выбор метода зависит от конкретной задачи и требуемой точности вычисления. Использование аналитических методов или численных методов вычисления интегралов позволяет решать различные математические задачи, в том числе моделировать физические процессы, изучать статистические закономерности или оптимизировать процессы в экономике.
Определенный интеграл и его вычисление
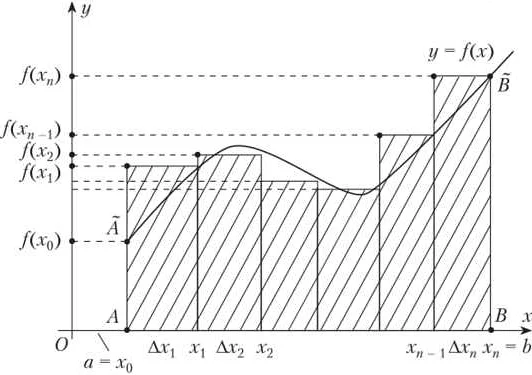
Определенный интеграл обозначается символом ∫ и имеет вид ∫ab f(x) dx, где f(x) — интегрируемая функция, a и b — границы интегрирования, x — переменная интегрирования.
Вычисление определенного интеграла сводится к нахождению площади под кривой, ограниченной графиком функции f(x), осью x и прямыми x=a и x=b. Для этого используется методы численного интегрирования, такие как метод прямоугольников, метод тrapezoidal, метод Симпсона и другие.
В основе данных методов лежит разбиение интервала интегрирования на равные или неравные отрезки и аппроксимация площади под кривой с помощью площадей прямоугольников, трапеций или парабол.
Точность вычисления определенного интеграла зависит от выбранного метода и числа разбиений. Чем больше разбиений, тем более точный результат можно получить.
Определенный интеграл имеет много практических применений, например, в экономике для вычисления общего дохода или затрат, в физике для определения площади под графиком скорости или ускорения, в статистике для нахождения вероятности события и многих других областях.
Неопределенный интеграл и его связь с производной
Пусть дана функция f(x). Неопределенный интеграл от f(x) обозначается как ∫f(x)dx и представляет собой множество всех функций F(x), для которых F'(x) = f(x), где F'(x) — производная функции F(x).
Таким образом, неопределенный интеграл позволяет найти класс функций, производные которых равны заданной функции f(x). При этом, так как производная неопределенного интеграла равна заданной функции f(x), то неопределенный интеграл является обратной операцией к производной.
Неопределенный интеграл имеет множество приложений в математике и физике. Он позволяет находить площади под кривыми, находить средние значения функций, решать дифференциальные уравнения и многое другое. Неопределенный интеграл является основой для определенного интеграла и находит широкое применение в различных областях науки и техники.
Применение интегралов в математике и физике
В математике интегралы применяются для нахождения площадей под кривыми и площадей между кривыми, для вычисления объемов тел и для решения различных задач, связанных с изменением величин. Например, интегралы используются для вычисления площади фигуры, ограниченной кривой и осями координат, или для нахождения объема тела, образованного вращением плоской фигуры вокруг оси. Также они применяются для определения центра масс объектов, что позволяет решать задачи, связанные с равновесием и движением тел.
В физике интегралы используются для решения задач, связанных с изменением физических величин со временем. Они позволяют вычислить массу, площадь, объем, траекторию и другие характеристики объектов и явлений. Например, интегралы применяются для нахождения работы, совершаемой при перемещении объекта под действием силы, или для определения количества вещества, протекающего через поверхность. Они также используются для описания траектории движения тела, изменения его скорости и ускорения.
Применение интегралов позволяет вычислять различные физические величины и решать задачи, связанные с измерением и изменением объектов и явлений в математике и физике. Оно имеет широкий спектр применений и играет важную роль в развитии этих наук.
Вычисление площадей и объемов
Интегралы также широко используются для вычисления площадей и объемов фигур и тел. Рассмотрим несколько примеров:
- Для вычисления площади фигуры, ограниченной графиком функции и осью абсцисс, можно использовать определенный интеграл. В этом случае функция, описывающая границы фигуры, будет являться подынтегральной функцией. Границы интегрирования будут соответствовать интервалу, на котором определена функция. Вычисляя интеграл, мы получим площадь фигуры под графиком функции.
- Аналогично можно вычислить площадь фигуры, ограниченной двумя функциями. В этом случае необходимо вычислить разность площадей фигур, ограниченных каждой функцией отдельно, и затем найти модуль этой разности.
- Для вычисления объема тела, полученного вращением кривой вокруг оси, можно использовать определенный интеграл. Функция, описывающая кривую, будет являться подынтегральной функцией. Границы интегрирования будут соответствовать интервалу, на котором определена функция. Вычисляя интеграл, мы получим объем тела.
- Аналогично можно вычислить объем тела, полученного вращением кривой вокруг другой оси. В этом случае необходимо вычислить разность объемов тел, полученных вращением кривой вокруг каждой оси отдельно, и затем найти модуль этой разности.
Интегралы позволяют точно вычислять площади и объемы фигур и тел, а также находить решения различных математических задач, связанных с этими величинами.
Определение центра масс

Математически, центр масс определяется следующим образом:
| Для системы из n точек | C_x = (m_1 * x_1 + m_2 * x_2 + … + m_n * x_n) / (m_1 + m_2 + … + m_n) |
| Для непрерывного объекта | C_x = (1 / M) * ∫(x * dm) |
где C_x — координата центра масс по оси x, x_i — координата i-ой точки по оси x, m_i — масса i-ой точки, M — общая масса объекта, dm — масса элемента объекта вдоль оси x.
Центр масс имеет ряд важных свойств:
- Центр масс всегда находится внутри или на границе объекта.
- Центр масс не зависит от выбора системы координат.
- Центр масс может не совпадать с физическим центром объекта, особенно если масса распределена неравномерно.
Интеграл используется для нахождения центра масс в различных областях математики и физики, включая механику, статику, динамику, термодинамику и т. д. Определение центра масс является важной концепцией, позволяющей анализировать и понимать движение и поведение объектов в пространстве.
Решение дифференциальных уравнений
Существует несколько методов решения дифференциальных уравнений:
- Метод разделения переменных. В этом методе уравнение приводится к виду, в котором все производные функции собраны в одной части уравнения, а все функции — в другой части. Затем производится интегрирование обеих частей, что позволяет найти функцию, удовлетворяющую уравнению.
- Метод вариации постоянной. В этом методе решение дифференциального уравнения ищется в виде функции, содержащей произвольную постоянную. Затем эта функция подставляется в исходное уравнение, и путем выбора различных значений постоянной находятся все возможные решения.
- Метод интегрирующего множителя. Этот метод позволяет решить линейные дифференциальные уравнения с постоянными коэффициентами. Он основан на нахождении специального множителя, который превращает данное уравнение в уравнение, интегрируемое в явном виде.
Решение дифференциальных уравнений широко применяется в физике, инженерии, экономике и других науках. Оно позволяет описывать и предсказывать различные процессы и явления, связанные с изменением функций во времени или пространстве.
Вопрос-ответ:
Зачем нужен интеграл в математике?
Интеграл — это математический инструмент, который позволяет находить площади под кривыми и вычислять некоторые другие важные характеристики функций. Интегралы широко применяются в различных областях науки, техники и экономики.
Как можно объяснить понятие интеграла простыми словами?
Интеграл — это способ нахождения площади под кривой. Мы разбиваем эту площадь на бесконечное количество очень маленьких частей и суммируем их. Интеграл также позволяет нам вычислять некоторые другие характеристики функций, такие как среднее значение или общее изменение.
Какие методы существуют для вычисления интегралов?
Существует несколько методов для вычисления интегралов. Один из наиболее распространенных методов — это метод Ньютона-Лейбница, который основан на нахождении первообразной функции и использовании ее значения в определенных пределах. Кроме того, существуют численные методы, такие как метод прямоугольников, метод трапеций и метод Симпсона, которые позволяют приближенно вычислять интегралы.
В каких областях науки и техники применяются интегралы?
Интегралы применяются во многих областях науки и техники. Например, в физике они используются для вычисления площадей под графиками зависимости физических величин, таких как скорость или ускорение. В экономике они применяются для определения общего изменения величин, таких как спрос или предложение. Также интегралы используются в теории вероятностей, геодезии, компьютерной графике и многих других областях.
Как можно объяснить понятие интеграла простыми словами?
Интеграл — это математическое понятие, которое позволяет найти площадь под кривой на графике функции. Он позволяет решать задачи, связанные с вычислением площади, объемов, скорости изменения и других величин.
В каких случаях используется интеграл в математике?
Интеграл применяется в различных областях математики и физики. Например, он используется для вычисления площади под кривой, нахождения объемов тел, определения среднего значения функции, решения дифференциальных уравнений и многих других задач.


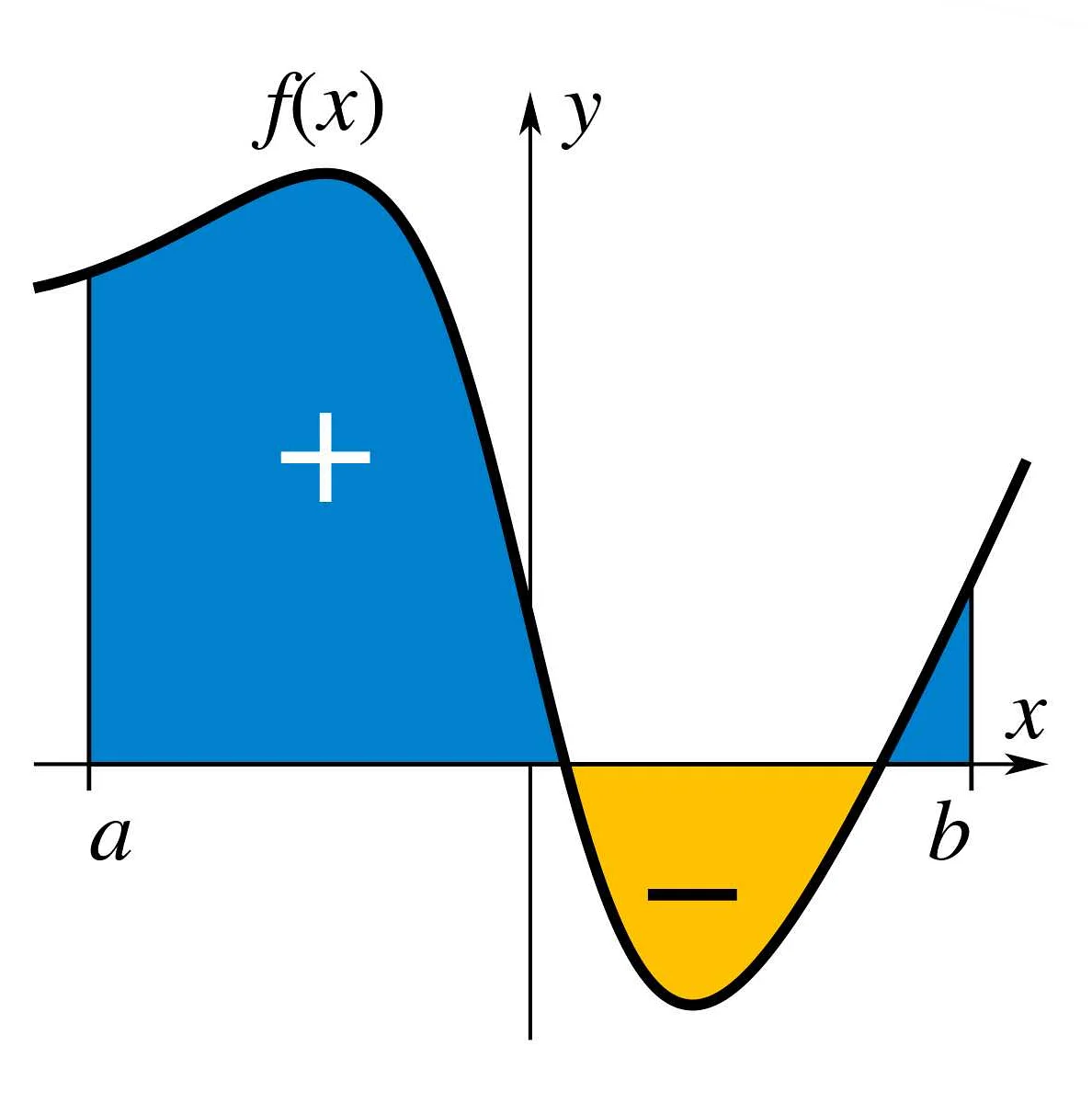
Интеграл — это математический объект, который позволяет нам находить площадь под кривой. Если представить, что у нас есть график функции на координатной плоскости, то интеграл позволяет найти площадь под этой кривой. Он также может использоваться для нахождения общего изменения функции в определенном интервале. Например, если у нас есть функция, описывающая скорость движения тела, то интеграл может помочь нам найти пройденное расстояние за определенное время. Интегралы широко используются в физике, экономике, статистике и других областях науки. Они помогают нам понять и описать различные явления и процессы в природе и обществе. Интегралы могут быть сложными и требовать математического аппарата, но их основная идея в том, чтобы найти площадь под кривой и использовать эту информацию для решения различных задач.
Спасибо автору за интересную и понятную статью! Я всегда слышала о понятии интеграла, но никогда не понимала, что оно на самом деле означает. Теперь стало все гораздо яснее. Интеграл — это не просто сумма, а способ определить площадь под кривой. Мне понравилось объяснение на примере задачи с движущейся машиной. Теперь я лучше понимаю, как использовать интеграл в реальной жизни. Это очень полезный инструмент, который помогает решать различные задачи, связанные с изменением величин. Статья была написана простым и доступным языком, что позволило мне легко усвоить материал. Я уже не боюсь термина «интеграл» и готова применять его в практике. Спасибо за разъяснения!