Что такое интеграл в математике 11 класс
Содержимое
- 1 Что такое интеграл в математике 11 класс
- 1.1 Интеграл в математике 11 класс: определение и примеры
- 1.2 Определение интеграла
- 1.3 Примеры интегралов
- 1.4 Свойства интеграла
- 1.5 Определенный интеграл
- 1.6 Неопределенный интеграл
- 1.7 Площадь и объемы фигур через интеграл
- 1.8 Теорема Ньютона-Лейбница
- 1.9 Вопрос-ответ:
- 1.10 Практическое применение интеграла
- 1.11 Видео по теме:
Интеграл в математике 11 класс — это понятие, которое описывает площадь под кривой графика функции. Важным инструментом для нахождения интегралов является определенный и неопределенный интеграл. Изучение интегралов позволяет решать задачи о нахождении площадей, длин дуг, объемов тел и многих других важных в математике величин.
Интеграл – одно из основных понятий математического анализа, изучаемое в 11 классе. Он является обратной операцией к дифференцированию и позволяет находить площадь под кривой, а также решать различные задачи, связанные с накоплением и изменением величин во времени или пространстве.
Определение интеграла основано на понятии предела и бесконечно малых величин. Интеграл разбивается на два вида: определенный и неопределенный. Определенный интеграл позволяет находить площадь под кривой на заданном интервале, а неопределенный интеграл используется для нахождения функции, производной которой является исходная функция.
Примеры использования интеграла в математике разнообразны. Он может использоваться для нахождения площади под различными геометрическими фигурами, включая окружности, эллипсы и прямоугольники. Также интеграл применяется для решения физических задач, например, для нахождения работы, совершенной силой, или для определения объема тела, образованного вращением кривой вокруг оси.
Интеграл обладает рядом свойств, которые позволяют упростить его вычисление. Некоторые из них включают линейность, свойство симметрии и формулу замены переменной. Эти свойства позволяют применять различные методы для нахождения интегралов и делают его важным инструментом для решения математических и физических задач.
Интеграл в математике 11 класс: определение и примеры
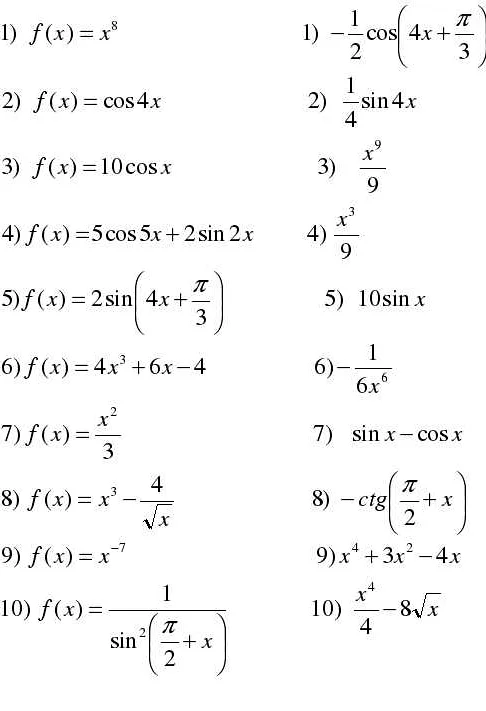
Определенный интеграл вычисляется на конечном интервале и имеет конкретные границы интегрирования. Неопределенный интеграл не имеет конкретных границ и является функцией, производной которой является исходная функция.
Интеграл обозначается символом ∫ (интегральное знак) и записывается в виде ∫ f(x) dx, где f(x) – подынтегральная функция, а dx – дифференциал переменной x.
Примеры задач, решаемых с помощью интеграла:
- Вычисление площади под кривой: для данной функции f(x) и заданного интервала [a, b] необходимо найти площадь фигуры, ограниченной графиком функции и осью OX в пределах этого интервала. Для этого используется определенный интеграл.
- Нахождение общего прироста величины: если задана функция f(t), описывающая изменение величины в течение времени t, то ее общий прирост можно найти, интегрируя функцию на заданном интервале времени.
- Решение дифференциальных уравнений: интегралы часто применяются для решения дифференциальных уравнений, которые описывают зависимость функции от ее производной.
Интеграл имеет множество свойств, которые облегчают его вычисление и применение в различных задачах. Например, интеграл линеен, то есть сумма интегралов двух функций равна интегралу их суммы. Также интеграл может быть использован для нахождения среднего значения функции на заданном интервале.
Определение интеграла
Интеграл является противоположным понятием к производной. В то время как производная показывает скорость изменения функции в каждой ее точке, интеграл позволяет найти накопленное изменение функции на заданном интервале.
Определенный интеграл обозначается символом ∫, где a и b – начальная и конечная точки интервала, а f(x) – интегрируемая функция.
Интеграл можно представить в виде:
∫[a, b] f(x) dx
Эта запись означает, что мы интегрируем функцию f(x) по переменной x на интервале [a, b]. Результатом вычисления интеграла будет число, которое представляет собой площадь под графиком функции f(x) на данном интервале.
Примеры интегралов

Ниже приведены несколько примеров вычисления определенных и неопределенных интегралов.
- Определенный интеграл:
- Вычисление определенного интеграла функции f(x) = x^2 на отрезке [0, 2]:
∫02 x^2 dx = [x^3/3] 02 = (2^3/3) — (0^3/3) = 8/3
- Вычисление определенного интеграла функции f(x) = x^2 на отрезке [0, 2]:
- Неопределенный интеграл:
- Вычисление неопределенного интеграла функции f(x) = 3x^2:
∫ 3x^2 dx = x^3 + C
где C — произвольная постоянная.
- Вычисление неопределенного интеграла функции f(x) = 3x^2:
Это лишь некоторые примеры применения интегралов в математике. Интегралы являются важным инструментом для решения различных математических задач и имеют широкий спектр применения в физике, экономике и других науках.
Свойства интеграла
Интеграл имеет ряд важных свойств, которые позволяют упрощать вычисления и делать определенные преобразования.
СвойствоФормулаЗначение
| Линейность | ∫(a*f(x) + b*g(x)) dx = a*∫f(x) dx + b*∫g(x) dx | Интеграл от линейной комбинации функций равен линейной комбинации интегралов от этих функций |
| Аддитивность | ∫(f(x) + g(x)) dx = ∫f(x) dx + ∫g(x) dx | Интеграл от суммы функций равен сумме интегралов от этих функций |
| Монотонность | Если f(x) ≤ g(x) на [a, b], то ∫f(x) dx ≤ ∫g(x) dx | Если одна функция не превосходит другую на определенном интервале, то интеграл от первой функции не превосходит интеграла от второй функции |
| Интегрирование по частям | ∫u(x) v'(x) dx = u(x) v(x) — ∫v(x) u'(x) dx | Позволяет связать интеграл с производной функции и упростить вычисления |
| Замена переменной | ∫f(g(x)) g'(x) dx = ∫f(u) du | Позволяет заменить переменную в интеграле и упростить его вычисление |
Знание и правильное применение этих свойств позволяет значительно облегчить вычисления в интегральном исчислении и повысить точность результатов.
Определенный интеграл
Определенный интеграл функции f(x) на отрезке [a, b] обозначается как ∫abf(x)dx и представляет собой предел интегральных сумм при их стремлении к нулю.
Определенный интеграл имеет следующие свойства:
- Линейность: ∫ab(c*f(x) + d*g(x))dx = c*∫abf(x)dx + d*∫abg(x)dx, где c и d — произвольные постоянные.
- Аддитивность: ∫abf(x)dx + ∫bcf(x)dx = ∫acf(x)dx, где a, b и c — произвольные числа, при этом a ≤ b ≤ c.
- Интегрирование по частям: ∫abu(x)v'(x)dx = u(x)v(x)|ab — ∫abv(x)u'(x)dx.
- Замена переменной: ∫abf(g(x))g'(x)dx = ∫g(a)g(b)f(u)du, где u = g(x).
Определенный интеграл позволяет решать задачи на вычисление площади фигур, нахождение среднего значения функции на отрезке, вычисление длины дуги функции, нахождение объема тела при вращении кривой вокруг оси и многие другие.
Неопределенный интеграл
Неопределенный интеграл обозначается символом ∫ и записывается как ∫f(x)dx, где f(x) – подынтегральная функция, а dx – дифференциал переменной x. Неопределенный интеграл удовлетворяет следующему свойству: если F(x) является первообразной функцией для f(x), то для любого x верно равенство ∫f(x)dx = F(x) + C, где C – произвольная постоянная.
Неопределенный интеграл позволяет найти множество функций, производная которых равна заданной функции. Для нахождения неопределенного интеграла необходимо применить соответствующие методы интегрирования, такие как интегрирование по частям, замена переменной или использование таблицы интегралов.
Примеры неопределенных интегралов:
ФункцияНеопределенный интеграл
| f(x) = x^n | ∫x^n dx = (x^(n+1))/(n+1) + C |
| f(x) = sin(x) | ∫sin(x) dx = -cos(x) + C |
| f(x) = e^x | ∫e^x dx = e^x + C |
Неопределенный интеграл является важным понятием в математике, так как он позволяет решать широкий спектр задач, связанных с нахождением площадей под кривыми, определением функций по их производным и многим другим.
Площадь и объемы фигур через интеграл

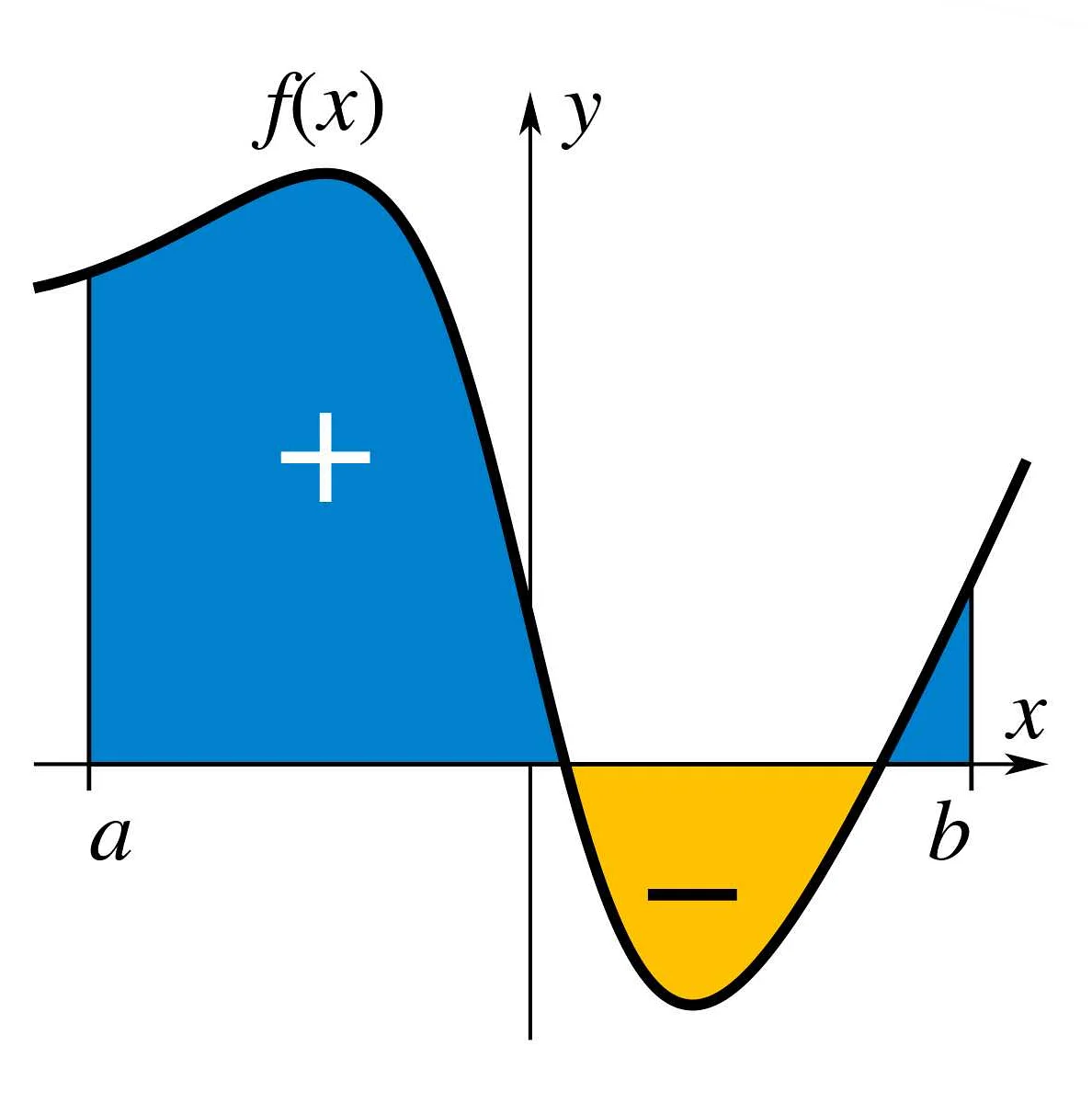
Для нахождения площади фигуры, ограниченной кривой и осью абсцисс, необходимо построить график этой кривой на заданном интервале и вычислить определенный интеграл от функции, задающей эту кривую. Таким образом, площадь фигуры будет равна значению определенного интеграла.
Аналогично, интеграл может быть использован для вычисления объемов фигур в трехмерном пространстве. Для этого необходимо построить график поверхности фигуры и вычислить определенный интеграл от функции, задающей эту поверхность. Таким образом, объем фигуры будет равен значению определенного интеграла.
Применение интеграла для нахождения площади и объема фигур позволяет решать задачи, связанные с вычислением площадей плоских и объемов пространственных фигур различной формы и сложности. Это важный инструмент в математике и науках, где требуется вычисление площадей и объемов для решения различных задач.
Теорема Ньютона-Лейбница

Пусть F(x) — непрерывная на отрезке [a, b] функция, и пусть f(x) — её производная на этом отрезке. Тогда для любой точки x из отрезка [a, b] справедливо следующее равенство:
∫(a→b) f(x) dx = F(b) — F(a)
То есть, значение определённого интеграла функции f(x) на отрезке [a, b] равно разности значений первообразной функции F(x) в точках a и b.
Теорема Ньютона-Лейбница позволяет вычислять определённые интегралы, зная функцию и её первообразную. Она также позволяет связать понятия площади и площади под графиком функции.
Теорема Ньютона-Лейбница является одной из основных теорем интегрального исчисления и является фундаментальным инструментом в решении задач нахождения площадей фигур и нахождения суммы бесконечных рядов.
Вопрос-ответ:
Как определить интеграл?
Интеграл определяется как предел суммы бесконечно малых приращений функции, умноженных на соответствующие бесконечно малые приращения независимой переменной.
Какие примеры использования интеграла в математике?
Интеграл используется для вычисления площадей фигур, нахождения объемов тел, решения дифференциальных уравнений, анализа функций и многих других математических задач.
Какие свойства имеет интеграл?
Интеграл обладает свойствами линейности, аддитивности, монотонности, инвариантности относительно параллельного переноса, инвариантности относительно замены переменной и неотрицательности.
Каково значение интеграла от постоянной функции?
Значение интеграла от постоянной функции равно площади прямоугольника, ограниченного графиком функции и осями координат.
Как вычислить интеграл от суммы двух функций?
Интеграл от суммы двух функций равен сумме интегралов от каждой функции по отдельности. Это свойство называется свойством аддитивности.
Практическое применение интеграла

Одним из применений интеграла является вычисление площади под кривой. Например, площадь под графиком функции может быть найдена с помощью определенного интеграла. Это особенно полезно при исследовании графиков функций и решении задач, связанных с геометрией.
Интеграл также используется в физике для вычисления работы, силы и энергии. Например, при вычислении работы силы можно использовать определенный интеграл, заменяя силу на функцию смещения. Это позволяет определить работу, совершенную силой по перемещению тела.
Еще одним практическим применением интеграла является вычисление объемов тел. Например, объем фигуры, ограниченной двумя или более кривыми, можно вычислить с помощью определенного интеграла. Это полезно при решении задач, связанных с геометрией и архитектурой.
Интеграл также применяется в экономике и финансах. Например, с помощью определенного интеграла можно вычислить средний доход или среднюю прибыль за определенный промежуток времени. Это позволяет анализировать динамику доходов и прибыли в различных сферах деятельности.
Таким образом, интеграл имеет широкое применение в различных областях науки и техники. Он позволяет решать задачи, связанные с геометрией, физикой, экономикой и другими дисциплинами, где требуется вычисление площадей, объемов, работ и других величин.
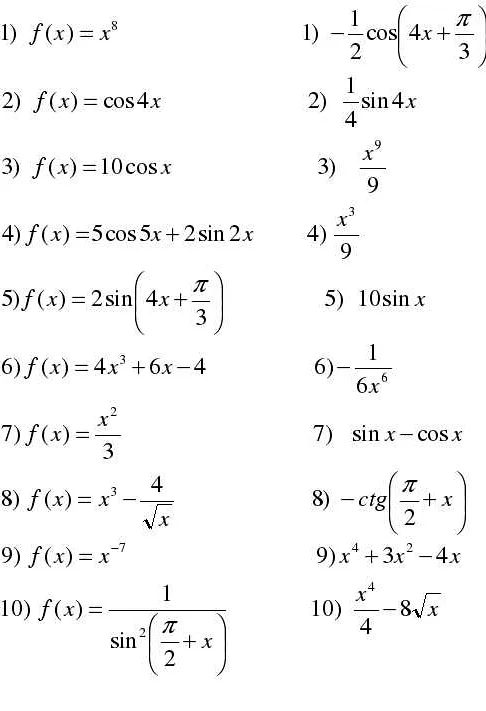



Статья очень понравилась! Она отлично объясняет, что такое интеграл в математике 11 класса. Я всегда считала, что интегралы — это сложно и непонятно, но благодаря данной статье многое прояснилось. Она содержит ясное определение интеграла и приводит несколько примеров, которые помогают лучше понять его суть. Особенно мне понравилось, что статья описывает свойства интеграла, такие как линейность и аддитивность. Это помогает лучше понять, как работает интеграл и какие операции с ним можно производить. В целом, статья очень информативна и полезна для тех, кто изучает математику на уровне 11 класса. Спасибо автору за прекрасное объяснение!
Статья дает хороший обзор на тему интеграла в математике для 11 класса. Рассмотрение определения интеграла и его свойств было очень информативным и понятным. Примеры, приведенные в статье, помогли мне лучше понять применение интеграла в различных задачах. Особенно мне понравилось объяснение о связи между интегралом и площадью под кривой. Благодаря этой статье я получила более глубокое понимание интеграла и его важности в математике. Рекомендую всем студентам 11 класса ознакомиться с этой статьей для успешной подготовки к экзамену.