Математика 6 класс как решать уравнения с дробями

Узнайте, как решать уравнения с дробями в математике для 6 класса. Научитесь приводить дроби к общему знаменателю, упрощать выражения и находить значения неизвестных в уравнениях. Получите подробные пошаговые инструкции и примеры решения уравнений с дробями.

Решение уравнений с дробями является важным этапом в изучении математики для учеников 6 класса. Понимание этого материала поможет им освоить базовые навыки алгебры и применять их в решении практических задач.

Уравнения с дробями представляют собой математические выражения, в которых присутствуют числа и операции с дробями. Решение таких уравнений требует знания основных правил арифметики, а также способности проводить манипуляции с дробями.

Основной шаг при решении уравнений с дробями — избавление от дробей. Для этого необходимо привести уравнение к общему знаменателю и выполнить арифметические операции над числителями. Затем полученное уравнение можно решить с помощью известных методов, таких как перенос в одну сторону или применение соответствующих формул и правил.

Приведенные алгоритмы помогут ученикам 6 класса научиться решать уравнения с дробями и применять полученные знания в практических ситуациях. Это не только разовьет их аналитическое мышление, но и подготовит к дальнейшему изучению математики на более сложных уровнях.

Определение уравнений с дробями

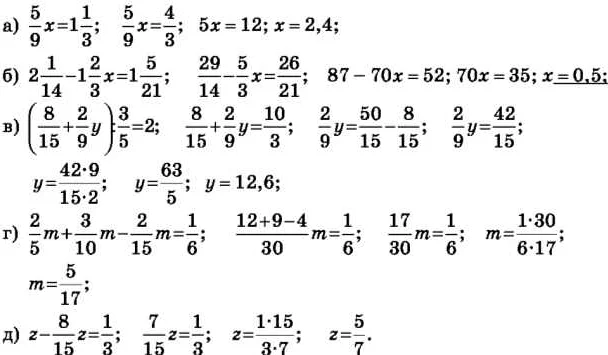
Решение уравнения с дробями состоит в нахождении значения переменной или переменных, которые удовлетворяют данному уравнению. Для этого необходимо привести уравнение к более простому виду, избавившись от дробей и сократив выражения.

Примеры уравнений с дробями:

1) x/a = b, где a и b — числа, x — переменная.

2) (a/b) + (c/d) = e, где a, b, c, d и e — числа.

3) (a/b) — (c/d) = e, где a, b, c, d и e — числа.

4) (a/b) * (c/d) = e, где a, b, c, d и e — числа.

5) (a/b) / (c/d) = e, где a, b, c, d и e — числа.

Для решения уравнений с дробями необходимо применять различные методы и правила алгебры, такие как сокращение дробей, общий знаменатель, умножение на обратное число и другие.

Видео по теме:

Как преобразовать уравнения с дробями

Уравнения с дробями могут быть сложными для решения, но с помощью определенных преобразований и правил их можно упростить и найти их решение. В этом разделе мы рассмотрим основные шаги, которые помогут вам преобразовать уравнения с дробями.

Шаг 1: Определите общий знаменатель

Для начала определите общий знаменатель для всех дробей в уравнении. Для этого найдите наименьшее общее кратное (НОК) знаменателей всех дробей. Если знаменатели уже одинаковы, то вы можете пропустить этот шаг.

Шаг 2: Приведите дроби к общему знаменателю

Умножьте каждую дробь на такое число, чтобы ее знаменатель стал равен общему знаменателю. В результате всех преобразований все дроби будут иметь одинаковый знаменатель.

Шаг 3: Упростите уравнение

Приведите уравнение к более простому виду, упрощая числители и знаменатели дробей. Сократите, если это возможно, общие множители числителя и знаменателя в каждой дроби.

Шаг 4: Решите получившееся уравнение

После преобразований и упрощений вы получите уравнение без дробей. Решите его, используя стандартные методы решения уравнений, такие как выражение переменной или применение алгебраических операций.

Следуя этим шагам, вы сможете преобразовать уравнения с дробями и найти их решение. Практика и опыт помогут вам освоить эту тему и успешно решать подобные уравнения.

Сложение и вычитание уравнений с дробями

Для решения уравнений с дробями, вам необходимо уметь складывать и вычитать дроби. Сложение и вычитание дробей осуществляется следующим образом:

ДействиеПримерРезультат

Сложение	1/2 + 1/3	5/6
Вычитание	2/3 — 1/4	5/12

Для сложения и вычитания дробей с одинаковыми знаменателями, вы просто складываете или вычитаете числители, оставляя знаменатель без изменений. Например, чтобы сложить 1/2 и 1/3, вы складываете числители: 1/2 + 1/3 = 5/6.

Если дроби имеют разные знаменатели, вы должны привести их к общему знаменателю, а затем сложить или вычесть числители. Например, чтобы вычесть 1/4 из 2/3, вам необходимо привести их к общему знаменателю, который равен 12: 2/3 — 1/4 = 8/12 — 3/12 = 5/12.

Помните, что после сложения или вычитания дробей, результат может потребовать сокращения. Для сокращения дробей, необходимо найти общий делитель числителя и знаменателя, и разделить их на этот делитель. Например, если результат сложения дробей равен 5/6, вы можете сократить его до 5/3 путем деления числителя и знаменателя на 2.

Теперь вы знакомы с основными правилами сложения и вычитания уравнений с дробями. Практикуйтесь в их применении, чтобы улучшить свои навыки в решении уравнений с дробями.

Вопрос-ответ:

Как решить уравнение с дробью, если в нём есть сложение или вычитание дробей?

Для решения уравнений с дробями, содержащих сложение или вычитание, обычно используют метод перевода уравнения в вид, где дроби имеют общий знаменатель. Затем сложение и вычитание выполняются с учетом общего знаменателя. После этого уравнение приводится к виду без дробей, и решается обычными методами.

Как решить уравнение с дробью, если в нём есть умножение или деление дробей?

Для решения уравнений с дробями, содержащих умножение или деление, обычно используют метод перевода уравнения в вид, где дроби умножаются или делятся без изменения знаменателя. Затем действия с дробями выполняются, и уравнение приводится к виду без дробей. После этого решается обычное уравнение без дробей.

Как решить уравнение с дробью, если в нём есть дробь в степени?

Для решения уравнений с дробями, содержащих дробь в степени, можно использовать метод перевода дроби в степени в обыкновенную десятичную дробь. Затем степень приводится к виду обыкновенной десятичной дроби, и уравнение решается обычными методами для уравнений с обыкновенными десятичными дробями.

Как решить уравнение с дробью, если в нём есть неизвестная в знаменателе?

Для решения уравнений с дробями, содержащих неизвестную в знаменателе, обычно используют метод перевода уравнения в вид, где знаменатель можно выразить через неизвестную. Затем уравнение приводится к виду без дробей, и решается обычными методами.

Как решить уравнение с дробью, если в нём есть несколько дробных выражений?

Для решения уравнений с несколькими дробными выражениями можно использовать метод перевода уравнения в вид, где дробные выражения суммируются или вычитаются. Затем суммирование или вычитание выполняются с учетом общего знаменателя. После этого уравнение приводится к виду без дробей, и решается обычными методами.

Умножение и деление уравнений с дробями

При умножении дробей в уравнении необходимо умножить каждую дробь на одно и то же число, чтобы получить равносильное уравнение. Помните, что дробь может быть записана в виде числителя и знаменателя.

Например, рассмотрим уравнение:

2/3 * x = 4/5

Чтобы избавиться от дробей, нужно умножить обе дроби на общий знаменатель, который в данном случае равен 15:

15 * (2/3) * x = 15 * (4/5)

Получаем:

10x = 12

Далее, чтобы найти значение переменной x, нужно разделить обе части уравнения на коэффициент перед переменной, в данном случае на 10:

x = 12/10

x = 6/5

Таким образом, решение уравнения равно x = 6/5.

При делении дробей в уравнении, необходимо умножить первую дробь на обратную второй дроби. Помните, что обратная дробь получается путем перестановки числителя и знаменателя.

Например, рассмотрим уравнение:

(3/4) / x = 5/6

Чтобы избавиться от деления, нужно умножить первую дробь на обратную второй дроби:

(3/4) * (6/5) = 5/6 * x

Получаем:

18/20 = 5/6 * x

Далее, чтобы найти значение переменной x, нужно умножить обе части уравнения на обратную дробь перед переменной, в данном случае на 6/5:

18/20 * (6/5) = 5/6 * x * (6/5)

Получаем:

18/20 * 6/5 = x

54/100 = x

Таким образом, решение уравнения равно x = 54/100.

Умножение и деление уравнений с дробями требует внимательности и точности в выполнении математических операций. Не забывайте проверять полученное решение, подставляя найденное значение переменной обратно в исходное уравнение.

Решение уравнений с дробями методом замены

Для решения уравнений с дробями можно использовать метод замены. Этот метод заключается в замене дроби на новую переменную, чтобы упростить уравнение и избавиться от дроби.

Шаги для решения уравнения с дробями методом замены:

Шаг 1: Представьте уравнение в виде общего вида с дробью.

Пример: 3/4x + 1/2 = 5/6

Шаг 2: Замените дробь на новую переменную.

Пусть новая переменная равна u: u = 3/4x

Шаг 3: Представьте уравнение с использованием новой переменной.

После замены дроби на новую переменную, уравнение примет вид: u + 1/2 = 5/6

Шаг 4: Решите уравнение относительно новой переменной.

Решим уравнение u + 1/2 = 5/6 относительно u. Для этого вычтем 1/2 из обеих частей уравнения: u = 5/6 — 1/2

Шаг 5: Найдите значение переменной u.

Вычислим правую часть уравнения: 5/6 — 1/2 = 5/6 — 3/6 = 2/6 = 1/3

Таким образом, u = 1/3

Шаг 6: Найдите значение исходной переменной.

Исходная переменная равна 3/4x. Подставим значение u вместо дроби: 1/3 = 3/4x

Умножим обе части уравнения на 4/3, чтобы избавиться от дроби: 4/3 * 1/3 = 4/9

Таким образом, 3/4x = 4/9

Шаг 7: Решите уравнение относительно исходной переменной.

Решим уравнение 3/4x = 4/9 относительно x. Для этого умножим обе части уравнения на 4/3: (3/4x) * (4/3) = (4/9) * (4/3)

Упростим выражение: x = 16/27

Шаг 8: Проверьте полученное значение.

Подставим x = 16/27 в исходное уравнение: 3/4 * (16/27) + 1/2 = 5/6

Выполним вычисления: (3/4) * (16/27) + 1/2 = 48/108 + 54/108 = 102/108 = 17/18

Таким образом, решением исходного уравнения 3/4x + 1/2 = 5/6 является x = 16/27.

Решение уравнений с дробями методом сокращения

Уравнения с дробями могут быть сложными для решения, но метод сокращения может помочь сделать процесс более простым и понятным. Этот метод основан на идее сокращения общих множителей числителя и знаменателя дроби.

Для начала, перепишем уравнение с дробями в виде обычного уравнения, умножив каждую дробь на общий знаменатель. Затем приведем дроби к общему знаменателю, выделим общие множители числителей и знаменателей и сократим их. После сокращения полученные уравнения будут проще для решения.

Давайте рассмотрим пример:

Решим уравнение: 3/4x + 2/5 = 7/10

1. 1. Умножим каждую дробь на общий знаменатель 20:

20 * (3/4)x + 20 * (2/5) = 20 * (7/10)

1. 1. Приведем дроби к общему знаменателю и сократим общие множители числителей и знаменателей:

15x + 8 = 14

1. 1. Выразим x:

15x = 14 — 8

15x = 6

x = 6/15

x = 2/5

Таким образом, решением уравнения является x = 2/5.

Использование метода сокращения упрощает процесс решения уравнений с дробями и позволяет получить более простой ответ. Однако, важно помнить, что при решении уравнений с дробями необходимо быть внимательными и аккуратными при работе с числителями и знаменателями.

Примеры решения уравнений с дробями

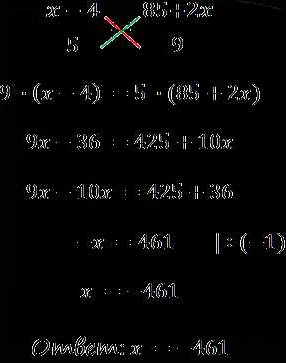
Дроби могут быть присутствовать в уравнениях, как коэффициенты, так и неизвестные значения. Решение таких уравнений требует определенных навыков работы с дробями. Рассмотрим некоторые примеры решения уравнений с дробями.

Пример 1: Решить уравнение: 2/x = 3/4

Для решения данного уравнения, необходимо привести обе дроби к общему знаменателю. В данном случае, общим знаменателем будет 4x. Умножим числитель и знаменатель первой дроби на 2, чтобы получить общий знаменатель:

2/x * 2/2 = 3/4

4/2x = 3/4

Теперь, умножим числитель и знаменатель второй дроби на x:

4/2x = 3/4 * x/x

4/2x = 3x/4x

Теперь, у нас есть две дроби с общим знаменателем. Составим уравнение:

4 = 3x/2

Умножим обе части уравнения на 2, чтобы избавиться от знаменателя:

4 * 2 = 3x/2 * 2

8 = 3x

Теперь, разделим обе части уравнения на 3, чтобы найти значение x:

8/3 = 3x/3

8/3 = x

Таким образом, решением уравнения является x = 8/3.

Пример 2: Решить уравнение: (2/3)x — 1/4 = 1/2

Для решения данного уравнения, необходимо избавиться от дробей в левой части, приведя их к общему знаменателю. В данном случае, общим знаменателем будет 12. Умножим первую дробь на 4/4 и вторую дробь на 6/6:

(2/3)x * 4/4 — 1/4 = 1/2 * 6/6

8/12x — 1/4 = 6/12

Теперь, у нас есть уравнение с дробью в левой части и десятичной дробью в правой части. Чтобы избавиться от дроби в левой части уравнения, умножим обе части уравнения на 12:

12 * (8/12x) — 12 * (1/4) = 12 * (6/12)

8x — 3 = 6

Теперь, сложим -3 с 6:

8x — 3 + 3 = 6 + 3

8x = 9

И, наконец, разделим обе части уравнения на 8, чтобы найти значение x:

8x/8 = 9/8

x = 9/8

Таким образом, решением уравнения является x = 9/8.

Практические задания по решению уравнений с дробями

1. Решите уравнение: 3/4x + 1/2 = 5/8

2. Найдите значение x, если 2/3x — 1/4 = 5/6

3. Решите уравнение: 4/5t — 1/3 = 3/10

4. Найдите значение x, если 1/2x — 1/3 = 2/5

5. Решите уравнение: 3/7z — 2/5 = 1/14

Для каждого задания напишите свое решение. Проверьте свои ответы и убедитесь, что они правильные. Если у вас возникли сложности, обратитесь к учебнику или преподавателю для получения дополнительной помощи.

ЗаданиеУравнение

1	3/4x + 1/2 = 5/8
2	2/3x — 1/4 = 5/6
3	4/5t — 1/3 = 3/10
4	1/2x — 1/3 = 2/5
5	3/7z — 2/5 = 1/14