Определите во сколько раз нужно увеличить длину математического маятника чтобы частота его колебаний

Узнайте, как изменяется частота колебаний математического маятника в зависимости от изменения его длины. Определите, во сколько раз нужно увеличить длину маятника, чтобы его частота колебаний увеличилась или уменьшилась. Подробное объяснение и примеры.

Математический маятник — это универсальное средство для изучения основных законов механики. Его колебания зависят от массы груза и длины подвеса. Частота колебаний математического маятника определяется длиной подвеса и силой тяжести. Иногда возникает необходимость изменить частоту колебаний маятника, и для этого можно воспользоваться простым способом — увеличить длину подвеса.

Увеличение длины математического маятника ведет к увеличению его периода колебаний. Период колебаний — это время, за которое математический маятник совершает один полный цикл колебаний. Чем длиннее подвес, тем больше времени требуется маятнику для совершения одного полного колебания. Таким образом, увеличение длины подвеса приводит к уменьшению частоты колебаний маятника.

Частота колебаний математического маятника выражается в герцах (Гц) и определяется как обратная величина периода колебаний. То есть, если увеличить длину подвеса в два раза, частота колебаний маятника уменьшится в два раза. Это свойство можно использовать для изменения частоты колебаний математического маятника в зависимости от требуемых условий исследования или эксперимента.

Важно помнить, что при увеличении длины подвеса математического маятника также меняется его амплитуда колебаний — расстояние, на которое маятник отклоняется от положения равновесия. Чем больше длина подвеса, тем меньше амплитуда колебаний. Поэтому при изменении длины подвеса необходимо также учитывать и эти особенности.

Итак, для изменения частоты колебаний математического маятника можно увеличить его длину подвеса. Этот простой метод позволяет достичь требуемых условий исследования или эксперимента, а также дает возможность получить более точные результаты в рамках изучения основных законов механики.

Математический маятник: как увеличить его длину для изменения частоты колебаний?

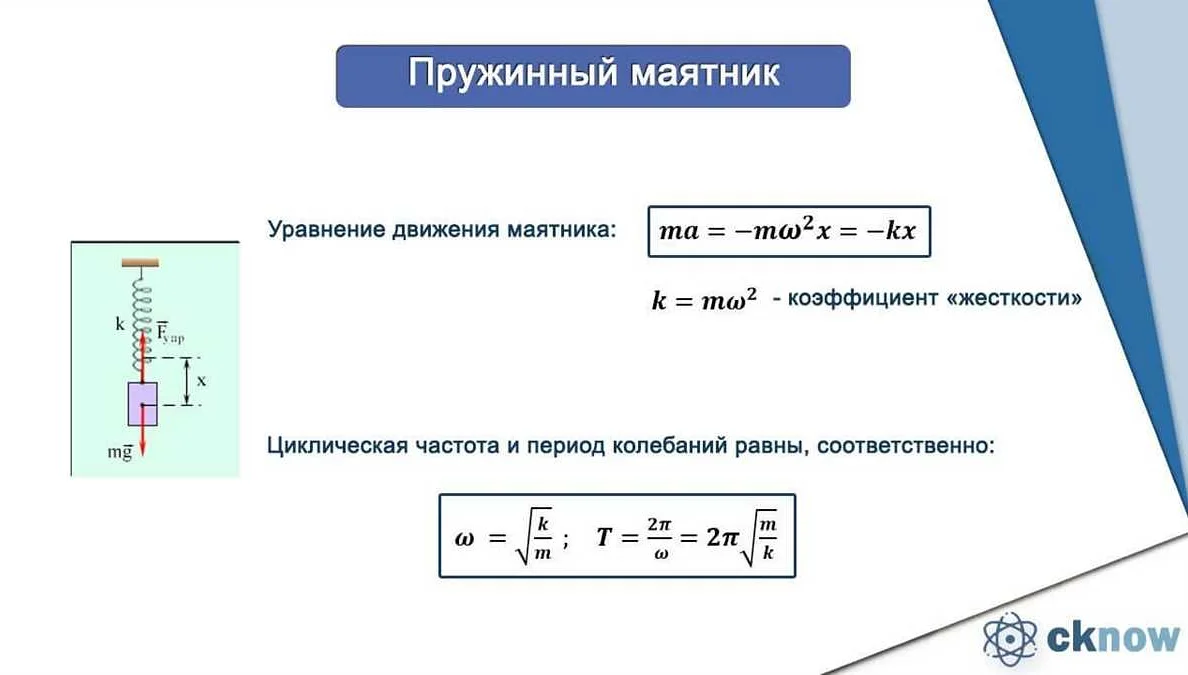
Частота колебаний математического маятника определяется формулой:

f = 1 / (2 * π * √(L / g))

где f — частота колебаний, L — длина маятника, g — ускорение свободного падения.

Таким образом, чтобы увеличить частоту колебаний математического маятника, необходимо уменьшить его длину. В то же время, если требуется увеличить длину маятника, чтобы уменьшить его частоту колебаний, можно воспользоваться следующими методами:

1. Установить маятник на достаточно длинной подвеске. Чем длиннее подвеска, тем длиннее будет маятник и, соответственно, меньше его частота колебаний.

2. Добавить грузы к маятнику. Дополнительные грузы на конце маятника увеличивают его эффективную длину, что приводит к уменьшению частоты колебаний.

3. Использовать удлинительную цепочку или шнур. Прикрепление маятника к удлинительной цепочке или шнуру позволяет увеличить его длину и, следовательно, снизить частоту колебаний.

Важно отметить, что в процессе изменения длины математического маятника необходимо учитывать его массу и ускорение свободного падения, так как они также влияют на частоту колебаний.

Итак, увеличение длины математического маятника позволяет изменить его частоту колебаний. Это может быть полезно в различных областях, таких как физика, инженерия, астрономия, где изучаются колебания и их свойства.

Видео по теме:

Влияние длины на частоту колебаний

Согласно формуле, частота колебаний математического маятника прямо пропорциональна квадратному корню из длины маятника и обратно пропорциональна квадратному корню из ускорения свободного падения. Таким образом, увеличение длины маятника приведет к увеличению его частоты колебаний.

Из этого следует, что при увеличении длины математического маятника он будет совершать меньшее количество колебаний за единицу времени, но каждое колебание будет занимать больше времени. Важно отметить, что длина маятника должна быть значительно меньше длины его нити, чтобы формула оставалась применимой.

Пример:

Пусть у нас есть математический маятник с длиной нити 1 метр. Если мы увеличим длину маятника до 2 метров, его частота колебаний увеличится в два раза по сравнению с изначальной частотой.

Таким образом, для изменения частоты колебаний математического маятника можно увеличить его длину.

Обратите внимание, что изменение других параметров, таких как масса маятника или силы трения, также может влиять на частоту колебаний, но в данном контексте рассматривается только влияние длины.

Понятие периода колебаний маятника

Период колебаний математического маятника зависит от его длины и ускорения свободного падения. Формула, описывающая период колебаний, выглядит следующим образом:

Формула:

T = 2π√(L/g)

Где:

• T — период колебаний;
• L — длина маятника;
• g — ускорение свободного падения.

Из формулы видно, что период колебаний маятника прямо пропорционален квадратному корню из его длины и обратно пропорционален квадратному корню из ускорения свободного падения. Таким образом, увеличение длины маятника приводит к увеличению его периода колебаний.

Зная формулу для периода колебаний маятника, можно определить, как изменить его частоту колебаний. Частота колебаний обратно пропорциональна периоду и обозначается символом f. Формула для частоты колебаний выглядит следующим образом:

Формула:

f = 1/T

Где:

• f — частота колебаний;
• T — период колебаний.

Таким образом, увеличение длины математического маятника приведет к увеличению его периода и, соответственно, уменьшению его частоты колебаний.

Как увеличить длину математического маятника?

Для увеличения длины математического маятника можно использовать несколько методов:

1. Использование более длинного подвеса:

Один из самых простых способов увеличить длину математического маятника — заменить его подвес на более длинный. При этом следует учесть, что длина подвеса измеряется от точки подвеса до центра масс маятника. Чем длиннее подвес, тем больше будет длина математического маятника.

2. Увеличение длины нити:

Если математический маятник имеет нить, то ее длину можно увеличить, чтобы увеличить длину маятника. Для этого можно использовать более длинную нить или добавить к существующей нити дополнительные сегменты. Увеличение длины нити приведет к увеличению длины всего математического маятника и, соответственно, увеличит его период колебаний.

3. Использование дополнительных грузов:

Еще одним способом увеличения длины математического маятника является добавление дополнительных грузов к его центру масс. При этом следует учесть, что масса грузов не должна слишком сильно изменять центр масс маятника, чтобы сохранить его гармонические свойства. Добавление грузов увеличит момент инерции маятника, что приведет к увеличению его периода колебаний.

Увеличение длины математического маятника позволяет изменить его частоту колебаний и создать условия для исследования различных физических и математических явлений.

Изменение частоты колебаний при увеличении длины

Для понимания взаимосвязи между длиной математического маятника и его частотой колебаний необходимо обратиться к формуле периода колебаний:

T = 2π√(L/g)

Где:

• T — период колебаний
• π — число π (приближенное значение 3,14)
• L — длина математического маятника
• g — ускорение свободного падения (приближенное значение 9,8 м/с²)

Из этой формулы видно, что период колебаний обратно пропорционален квадратному корню из длины маятника. То есть, если увеличить длину маятника, его период колебаний увеличится, что означает уменьшение его частоты колебаний.

Например, если исходная длина математического маятника равна 1 метру, то его период колебаний будет равен:

T = 2π√(1/9,8) ≈ 2π√(0,102) ≈ 2π × 0,319 ≈ 2,004 секунды

Если увеличить длину маятника до 2 метров, то его период колебаний изменится следующим образом:

T = 2π√(2/9,8) ≈ 2π√(0,204) ≈ 2π × 0,452 ≈ 2,841 секунды

Таким образом, увеличение длины математического маятника приводит к увеличению его периода колебаний, что в свою очередь изменяет его частоту колебаний. Это явление можно наблюдать в реальной жизни, например, в колебательных механических часах, где изменение длины маятника позволяет регулировать их точность и стабильность работы.

Взаимосвязь между длиной и периодом колебаний

Период колебаний математического маятника можно выразить следующей формулой:

T = 2π√(L/g)

Где:

• T — период колебаний;
• L — длина маятника;
• g — ускорение свободного падения.

Из этой формулы видно, что период колебаний математического маятника зависит от корня квадратного из длины маятника. Это означает, что увеличение длины маятника приведет к увеличению его периода колебаний.

Таким образом, если требуется увеличить период колебаний математического маятника, необходимо увеличить его длину. Это можно сделать, например, путем удлинения подвеса маятника или добавления дополнительных грузов на его конце.

Отношение длины маятника и его периода колебаний

Формула для вычисления периода колебаний математического маятника имеет вид:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Из этой формулы видно, что период колебаний математического маятника обратно пропорционален квадратному корню из его длины. То есть, если увеличить длину маятника, то его период колебаний увеличится, а если уменьшить длину, то период колебаний уменьшится.

Это означает, что для увеличения частоты колебаний математического маятника необходимо увеличить его длину. Таким образом, увеличение длины маятника приведет к уменьшению его периода колебаний и увеличению частоты колебаний.

Практическое применение увеличения длины маятника

Увеличение длины математического маятника может иметь практическое применение в различных областях науки и техники. Рассмотрим несколько примеров:

1. Физические исследования

   Увеличение длины маятника позволяет исследовать его поведение при различных условиях и вариациях параметров. Например, при увеличении длины маятника можно изучить зависимость его периода колебаний от массы груза или изменения силы тяжести. Такие исследования могут иметь применение в физике, механике и астрономии.

2. Образование и демонстрации

   Увеличение длины маятника позволяет создать более заметный и впечатляющий эффект при его колебаниях. Это может быть использовано в образовательных целях для демонстрации основных законов и принципов физики, а также для привлечения внимания научных экспериментов.

3. Технические приложения

   В некоторых технических системах, где требуется точное измерение времени или синхронизация процессов, могут использоваться математические маятники большой длины. Например, в часах с маятником длиной несколько метров можно достичь большей точности и стабильности показаний. Также длинные маятники могут использоваться в синхронизации механизмов, например, в метрономах.

Таким образом, увеличение длины математического маятника имеет широкие практические применения в различных областях науки и техники. Это позволяет исследовать его свойства, использовать в образовательных целях и применять в технических системах для улучшения точности и стабильности измерений.

Вопрос-ответ:

Как увеличить длину математического маятника?

Длину математического маятника можно увеличить путем увеличения длины подвеса или длины самого маятника.

Зачем нужно увеличивать длину математического маятника?

Увеличение длины математического маятника позволяет изменить его частоту колебаний и сделать их более медленными.

Какие методы можно использовать для увеличения длины математического маятника?

Для увеличения длины математического маятника можно использовать различные методы, включая удлинение подвеса или установку дополнительных элементов для увеличения длины маятника.

Как изменится частота колебаний математического маятника при увеличении его длины?

При увеличении длины математического маятника его частота колебаний уменьшится.

Какой эффект достигается при увеличении длины математического маятника?

Увеличение длины математического маятника позволяет увеличить его период колебаний и сделать их более медленными.

Как увеличить длину математического маятника?

Для увеличения длины математического маятника необходимо увеличить длину его подвеса. Это можно сделать, например, добавив к подвесу дополнительные элементы, такие как проволочные кольца или цепочки. Также можно использовать специальные удлинители для подвеса маятника.