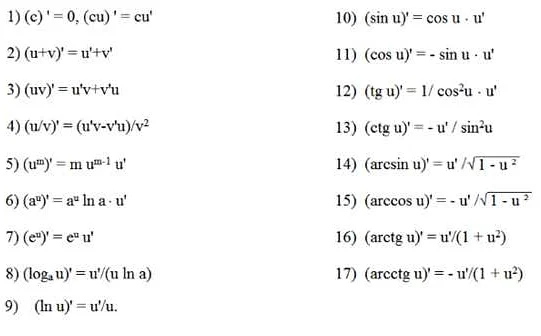Какое из перечисленных математических понятий является ключевым в решении задач?

Узнайте какое из перечисленных математических понятий — функция, гипотенуза, производная, интеграл — является ключевым в математике и как оно используется в решении различных задач.

Математика является одним из самых интересных и сложных предметов в школьной программе. В процессе обучения мы знакомимся с различными математическими понятиями, которые нужно понимать и уметь применять в жизни. Но какое из этих понятий является наиболее важным и зачем оно нужно? На этот вопрос мы попытаемся ответить в данной статье.

Перед нами стоит выбор из множества понятий: арифметика, геометрия, алгебра, тригонометрия и математический анализ. Каждое из них имеет свои достоинства и применение в реальной жизни. Но существует такое математическое понятие, которое важно для практически всех наук и применений в жизни. Это понятие — дробь.

Дробь – это математическое понятие, которое появляется в решении многих простых и сложных задач. Оно необходимо в физике, химии, экономике, географии и многих других науках. Дроби используются для определения пропорций, процентных соотношений, решения уравнений и многих других задач.

Какое понятие из математики важнее всего?

Вопрос о том, какое понятие в математике является наиболее важным, может вызвать дискуссию среди ученых и математиков.

Возможно, наиболее важным понятием в математике является алгебра. Она является основой для многих других областей математики, таких как геометрия, теория чисел, теория вероятностей и других. Без алгебры мы не могли бы решать уравнения, находить корни многочленов и строить графики функций. Алгебра является инструментом для решения математических проблем и играет важную роль в науке и технологии.

Однако, можно утверждать, что геометрия играет такую же важную роль, как и алгебра, поскольку она позволяет нам рассматривать форму и пространство, изучать свойства фигур и решать геометрические задачи. Геометрия также связана с физикой и инженерией и используется для построения моделей, например, для разработки проектов зданий и мостов.

Некоторые ученые утверждают, что теория чисел является наиболее важной областью математики, так как она изучает свойства и отношения между целыми числами и является основой для шифрования электронных сообщений и технологии криптографии.

Таким образом, можно сделать вывод, что определить, какое понятие в математике является наиболее важным, довольно сложно и зависит от того, какую задачу мы хотим решить. Каждая область математики имеет свои особенности и применения в науке и технологии.

Зачем нужно знать важные математические понятия?

Математика – это универсальный язык, используемый для описания мира и решения практических задач. Знание важных математических понятий позволяет взглянуть на мир с более точной и профессиональной точки зрения.

В повседневной жизни мы часто сталкиваемся с решением математических задач – начиная от расчета доставки, заканчивая решением сложных финансовых расчетов. Знание важных математических понятий помогает более точным образом решать задачи и избежать ошибок.

Кроме того, знание математики необходимо для понимания многих других наук, таких как физика, химия, экономика и информационные технологии.

Наконец, важные математические концепции также являются основой для более сложных математических теорем и моделей, которые находят применение в науке, технологиях и бизнесе.

Таким образом, знание важных математических понятий является необходимым для успешного функционирования в современном обществе и развития профессиональных навыков.

Самое важное математическое понятие

Математика изучает законы и отношения между числами, величинами и формулами. В этой науке есть множество понятий, которые могут быть важными в различных областях знаний. Однако, некоторые математические понятия можно считать основными и без которых не обойтись в решении большинства задач.

Самым важным математическим понятием можно считать арифметику – науку о числах и арифметических операциях над ними. Это базовое понятие позволяет проводить простейшие математические вычисления и решать многие повседневные задачи.

Другим важным понятием является геометрия – наука о фигурах и их свойствах. Геометрия используется в различных областях, например, при проектировании зданий и создания компьютерных игр. Это понятие также является основополагающим для изучения других областей математики, таких как алгебра и тригонометрия.

• Важными математическими понятиями также являются:
• Алгебра – наука об алгебраических структурах и операциях, таких как сложение, вычитание, умножение и деление;
• Тригонометрия – наука о тригонометрических функциях и углах;
• Математический анализ – наука о пределах, производных и интегралах.

В итоге, выбор самого важного математического понятия зависит от конкретной области знаний и задач, которые нужно решать. Однако, арифметика и геометрия – это базовые знания, которые обязательно должны быть владеемыми каждым человеком.

Почему именно это понятие важно?

Математическое понятие – это основа изучения математики. Однако, в каждой области математики существуют конкретные понятия, которые необходимы для понимания теории и решения задач. Среди этих понятий можно выделить такие, как: функция, дифференциал, интеграл, графы и другие. Важность каждого из этих понятий определяется областью математики, в которой оно используется.

Одним из наиболее важных математических понятий является функция. Функции используются практически во всех областях математики, начиная от арифметики и геометрии, заканчивая высшей алгеброй и математическим анализом. Функции используются для описания зависимостей между различными величинами и являются основой для их дальнейшего анализа и оптимизации.

Особым значением функции обладает в математическом анализе, где она рассматривается как основной объект изучения. Именно на основе функций строится теория дифференциальных и интегральных уравнений, которые находят применение в таких областях, как физика, экономика, химия и другие.

Также, функции используются в алгоритмах и программировании для описания действий и операций, выполняемых компьютером. Поэтому знание понятия функции является основным для всех, кто хочет заниматься программированием или работать со сложными алгоритмами.

В итоге, можно сказать, что понятие функции является основным и наиболее важным в математике. Оно является основой для построения целого ряда важных теорий и методов, которые находят применение в различных областях знаний и наук.

Как это понятие связано с другими изучаемыми в математике?

Математика – наука, которая исследует различные стороны и аспекты математических понятий. Отдельно взятые понятия представляют собой важные элементы теории, а в совокупности они образуют единую систему, в которой каждое понятие связано с другими.

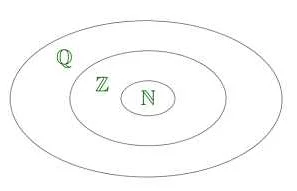
Например, понятие числа является одним из основных понятий математики – оно входит во многие математические теории: алгебру, геометрию, топологию, математический анализ и др.

Теория вероятности, которая изучает случайные явления, также тесно связана с понятием числа. В простейшем случае, когда вероятность равновероятных исходов, вероятность события вычисляется как отношение количества благоприятствующих исходов к общему числу исходов.

Операции над числами, такие как сложение, вычитание, умножение и деление, также тесно связаны с другими понятиями в математике, например, с алгеброй и теорией чисел.

Таким образом, понятия в математике образуют единую систему, где каждое понятие тесно связано с другими, и изучение каждого понятия позволяет лучше понимать и использовать другие понятия в математике.

В каких областях науки и технологий используется данное понятие?

Математика является основой многих наук и технологий, поэтому понятия, относящиеся к математике, используются в различных областях науки и технологий. Например, евклидова геометрия используется в физике, инженерии и архитектуре.

Арифметика и алгебра широко используются в экономике и финансах. Эти понятия позволяют производить точные расчеты и прогнозировать тенденции на рынке.

Теорияграфов и комбинаторика необходимы для решения задач в компьютерной науке и информационных технологиях, таких как поиск оптимальных маршрутов, генетические алгоритмы и криптография.

Теория вероятностей и математическая статистика используются в науке о данных для анализа и прогнозирования, в машинном обучении и в исследовании случайных процессов.

Также понятия математики используются в медицине, биологии и экологии, например, для моделирования и анализа данных в генном анализе и изучении популяций животных.

Каковы последствия непонимания данного понятия?

Непонимание математического понятия может привести к различным проблемам в учении и практическом применении математики. Например, если не понимать понятия пропорций, то будет трудно решать задачи на расчеты процентов и долей. Если не понимать понятие функции, то будет сложно решать уравнения и задачи на определение закономерностей в данных.

Непонимание важных математических понятий может также привести к ограничениям в выборе будущей профессии. Например, если не понимать понятия дифференциации и интегрирования, то нельзя будет стать математиком, физиком или инженером.

Кроме того, непонимание математических понятий может отразиться на общественной жизни. Например, если большинство людей не понимает понятие процента или доли, то это может привести к неправильному распределению ресурсов или к неэффективному использованию денежных средств.

В связи с этим, необходимо уделять достаточное внимание учению математики и пониманию всех ее основных понятий.

Как можно научиться лучше понимать данное понятие?

Для того чтобы лучше понимать перечисленные математические понятия, необходимо обращаться к источникам, которые могут помочь в этом. В интернете существует множество материалов, посвященных каждому из этих понятий, например, уроков, видео, статей. Стоит отметить, что выбор качественных источников является очень важным шагом на пути к более глубокому пониманию математических понятий.

Другой важный способ улучшения своего понимания — практика. Для этого необходимо решать задачи, которые связаны с данным понятием, и не только в школе или университете. На сайтах, посвященных математике, можно найти множество задач, которые помогут прокачать свои знания и умения.

Также важно общаться с другими студентами и специалистами в данной области. Совместное изучение и обсуждение материалов может привести к новым открытиям и познаниям. Многие вузы предоставляют студентам исследовательские возможности и мероприятия, посвященные математике и другим наукам.

1. Итак, важнейшие способы улучшения понимания математических понятий:
2. Просмотр видео уроков и чтение качественных статей по теме;
3. Решение задач, связанных с понятием;
4. Совместное изучение и обсуждение материалов с другими студентами и специалистами.

Интересные факты о понятии «дифференциал»

Дифференциал – математический термин, который происходит от латинского языка и означает «различная форма». Он используется для описания производной функции в точке и показывает, как значение функции изменится, если производная ее изменится незначительно.

История дифференциала насчитывает более 300 лет. Формальное объяснение понятия дано в труде Готфрида Лейбница «Новый метод полагать максимумы и минимумы, а также точки перегибания всякого рода кривых». Эта работа вышла в свет в 1684 году, а первый учебник по дифференциальному исчислению Лейбница был издан лишь в 1693 году.

Применения дифференциала применяются в различных областях, включая физику, экономику, биологию и инженерные науки. Например, дифференциал используется в физике при расчете траектории движения тела, а в экономике – для моделирования спроса на товары и услуги.

• Правило Лопиталя – это один из самых широко используемых методов дифференцирования функций в математике.
• Дифференциальное уравнение – это математическое уравнение, связывающее зависимую переменную и ее производную. Они находят широкое применение в различных областях науки и техники для моделирования различных процессов.

Дифференциалы высших порядков – это обобщение дифференциала первого порядка, связывающее значение функции, ее производные и производные высших порядков. Они играют важную роль в теории управления, при решении дифференциальных уравнений второго и высших порядков, а также в других областях науки.

В целом, понятие дифференциала позволяет работать с непрерывными функциями и найти значения производных для любой точки на интервале определения функции. Поэтому это понятие является одним из самых важных в математическом анализе и имеет широкое применение в различных областях знаний и наук.

Как изменится мир, если никто не знает это понятие?

Математические понятия пронизывают каждый аспект нашей жизни, даже если мы об этом не задумываемся. Они напрямую связаны с научными и техническими достижениями, экономикой, финансами, медициной, астрономией и многим другим. Если какое-то из математических понятий перестанет быть известным, это повлечет за собой серьезные последствия.

Представим, что никто не знает понятия дроби. В таком случае, люди не смогут делить что-либо на несколько равных частей, и концепция денежных курсов, обмена валют и процентов на банковские вклады перестанет существовать.

Если никто не знает, что такое теорема Пифагора, то люди не смогут вычислить длину гипотенузы прямоугольного треугольника или построить устойчивую конструкцию зданий. Множество инженерных и строительных проектов станут невозможными.

Таким образом, потеря любого математического понятия повлечет за собой нарушение сложной сети взаимосвязей и ограничит нас в наших возможностях. Поэтому понимание и изучение математики важно не только для профессионалов в этой области, но и для общества в целом.

Видео по теме:

Вопрос-ответ:

Какое понятие математики является наиболее важным?

Такого однозначного ответа на этот вопрос нет, так как каждая область математики имеет свою значимость и применение. Однако, можно отметить, что фундаментальные понятия, такие как алгебра, геометрия и теория чисел, являются основой для многих других областей математики и широко применяются в реальной жизни.

Что такое алгебра и как ее применяют?

Алгебра — это отрасль математики, изучающая абстрактные системы и операции над ними. Она широко используется в науке, инженерии, экономике, информатике и других областях. Например, в экономике алгебра используется для анализа финансовых данных, а в информатике — для создания алгоритмов и баз данных.

Зачем изучать геометрию?

Геометрия — это область математики, изучающая пространственные фигуры и их свойства. Ее результаты широко применяются в перспективных технологиях, таких как виртуальная реальность и 3D-печать. Кроме того, знание геометрии полезно в повседневной жизни для решения задач, связанных с измерением и построением объектов, например, при ремонте или дизайне интерьера.

Какая область математики является наиболее сложной?

Сложность области математики зависит от уровня подготовки и личных интересов каждого человека. Однако, многие ученые считают, что топология — это одна из наиболее сложных и абстрактных областей, изучающая геометрические свойства фигур, которые сохраняются при их деформации. Ее результаты используются в физике, математической статистике и других областях.

Что такое исчисление вероятностей и как его применяют?

Исчисление вероятностей — это область математики, изучающая процессы случайных событий и вероятности их возникновения. Она находит применение в статистике, физике, биологии, экономике, финансах и других областях. Например, в статистике она используется для анализа данных об определенной совокупности и оценки вероятности определенного исхода.

Зачем изучать математику в школе и как она полезна в жизни?

Изучение математики в школе помогает развивать логическое мышление, абстрактное мышление, умение анализировать и решать проблемы. Эти навыки широко применяются в жизни, например, при планировании бюджета, выборе инвестиций, решении бытовых задач и других ситуациях. Кроме того, знание математики открывает доступ к многим профессиям, таким как ученый, инженер, программист, экономист и другие.

Какая область математики наиболее перспективная в будущем?

Сейчас существует множество перспективных областей математики, таких как теория игр, математическая биология, математическое моделирование и другие. Однако, можно отметить, что разработка и улучшение алгоритмов и их применения к решению реальных задач будет оставаться важным в будущем. Кроме того, развитие искусственного интеллекта и машинного обучения требует глубоких знаний в области математики, таких как алгебра, теория вероятностей и дифференциальные уравнения.

Развитие данного понятия в истории математики

Концепция числа является одной из основных областей математики, которая принимает участие вовлекая огромное количество других математических понятий, таких как геометрия, алгебра, теория вероятностей, и т.д. Развитие концепции числа началось с самых ранних форм цивилизации в древнем Египте и Месопотамии.

Древние культуры использовали различные методы для обозначения чисел, например египетские считали путем суммирования других чисел. Однако, наиболее известной была десятичная система счисления, которая была создана в Индии примерно в 500 году до н.э. и которая стала определяющей системой счета в математике.

Древнегреческие математики, такие как Пифагор и Евклид дали важный вклад в развитие концепции числа в математике. Они изучали свойства и отношения между числами и развивали теории, которые затем использовались для решения различных математических проблем.

В средневековой Европе, математика была связана с философией и теологией, и числа использовались для описания абстрактных идей. В 16-м веке Ренессанса способствовал развитию математики и концепции числа. Французский математик Рене Декарт использовал геометрию для описания алгебры, а Иоаннес Кеплер использовал числа для изучения законов движения планет.

В 20-м веке, с развитием вычислительной техники и появлением новых математических теорий, концепция числа была углублена и расширена. Сегодня числа используются для описания и решения сложных математических проблем во многих областях, начиная от экономики и физики, заканчивая астрономией и инженерией.

Стремиться ли нужно к полному пониманию данного понятия?

Математические понятия являются ключевыми в любом изучении математики. Общее понимание этих понятий необходимо для того, чтобы лучше понимать мир и решать сложные проблемы. Однако, вопрос о том, должны ли мы стремиться к полному пониманию каждого из этих понятий, остается открытым.

С одной стороны, более глубокое понимание математических понятий может помочь нам в повседневной жизни и в нашей будущей карьере. Например, понимание алгебры может помочь нам обрабатывать данные и решать проблемы в нашей работе. Кроме того, глубокое понимание математики может помочь нам развивать наши когнитивные способности.

С другой стороны, не всегда стремление к полному пониманию каждого математического понятия является необходимым. Некоторые понятия могут быть слишком сложными или абстрактными, чтобы их полностью понимать. Например, понимание основ дифференциального исчисления не всегда обязательно для людей, занятых в области права или медицины.

Таким образом, ответ на вопрос, нужно ли стремиться к полному пониманию математических понятий, не является простым. Он зависит от нашей профессии, интересов и уровня образования. Однако, никогда не будет лишним углубить свои знания и понимание в математических понятиях, если это возможно и полезно для нашей карьеры и жизни в целом.