Математике производное чисел это какой знак
Содержимое
- 1 Математике производное чисел это какой знак
В математике производное чисел показывает, как меняется число при изменении другого числа. Знак производной указывает на направление изменения числа: положительное значение говорит о возрастании числа, отрицательное значение — о убывании числа.
Производная числа – это одно из важнейших понятий математического анализа. Она позволяет изучать изменение функции в зависимости от значения ее аргумента. Производная числа определяет, как быстро меняется значение функции в данной точке. Знание производной позволяет понять, в какую сторону и насколько быстро функция растет или убывает в данной точке.
Знак производной числа играет важную роль в анализе функций. Он позволяет определить, в каких интервалах функция возрастает или убывает. Если производная числа положительна, то функция возрастает. Если производная числа отрицательна, то функция убывает. Знание знака производной числа позволяет понять, как функция меняет направление своего изменения в каждой точке.
Например, если производная числа положительна в интервале от 0 до 1, то это означает, что функция возрастает в этом интервале. Если производная числа отрицательна в интервале от 1 до 2, то функция убывает в этом интервале.
Определение знака производной числа может быть полезным при решении задач оптимизации. Например, если нужно найти максимум или минимум функции на заданном интервале, то можно использовать информацию о знаке производной числа, чтобы найти эти точки.
Определение производной числа
Производная числа может быть представлена в виде отношения двух приращений: изменение значения функции (дельта y) и изменение аргумента (дельта x). Формально производная числа f(x) в точке x может быть записана следующим образом:
f'(x) = lim[(f(x + Δx) — f(x)) / Δx], где Δx стремится к нулю.
Знак производной числа позволяет определить направление изменения функции в данной точке. Если производная числа положительна, то функция возрастает, если отрицательна — функция убывает. Если производная числа равна нулю, то функция имеет экстремум (максимум или минимум).
Понятие скорости изменения
Производная числа показывает, как изменяется значение функции в определенной точке. Она позволяет определить, в какую сторону и насколько быстро меняется значение функции при изменении аргумента.
Знак производной числа указывает на направление изменения функции. Если производная положительна, то значение функции возрастает. Если производная отрицательна, то значение функции убывает. Если производная равна нулю, то значение функции не изменяется.
Знание знака производной числа позволяет определить поведение функции и ее экстремумы. Например, если производная числа положительна слева от точки и отрицательна справа от точки, то в этой точке функция имеет максимум.
Таким образом, понятие скорости изменения и определение знака производной числа играют важную роль в анализе функций и решении задач, связанных с изменением величин.
Графическое представление производной
Производная числа в математике имеет графическое представление, которое позволяет наглядно представить изменение функции в каждой точке ее графика.
Для графического представления производной может использоваться график функции и ее касательные. Касательная к графику функции в определенной точке является прямой, которая касается графика в этой точке и имеет ту же самую наклонную, что и график функции в этой точке.
Если функция возрастает в какой-то точке, то касательная будет расположена ниже графика функции. Если функция убывает в точке, то касательная будет находиться выше графика. Если функция имеет экстремум (максимум или минимум) в точке, то касательная будет горизонтальной и проходить через эту точку.
Знак производной определяется с помощью графического представления производной. Если касательная расположена ниже графика функции, то производная положительна. Если касательная находится выше графика функции, то производная отрицательна. Если касательная горизонтальна, то производная равна нулю.
Пример возрастающей функцииПример убывающей функцииПример функции с экстремумом
График функции:  Касательная:
| График функции:  Касательная:
| График функции:  Касательная:
|
Формула производной

Формула для нахождения производной функции f(x) выглядит следующим образом:
- Если функция f(x) представлена в виде суммы степеней переменной x, то производная f'(x) равна сумме производных каждого слагаемого.
- Если функция f(x) представлена в виде произведения нескольких слагаемых, то производная f'(x) равна сумме произведений производных каждого слагаемого.
- Если функция f(x) представлена в виде частного двух функций, то производная f'(x) равна разности произведений производных числителя и знаменателя, деленных на квадрат знаменателя.
Формула производной позволяет найти значение производной функции в любой точке и определить ее знак. Если производная положительна, то функция возрастает, если отрицательна – убывает, если равна нулю – функция имеет экстремум.
Как определить знак производной

Знак производной функции важен для определения поведения функции в заданной точке. Знак производной показывает, убывает функция или возрастает в данной точке. Для определения знака производной необходимо выполнить следующие шаги:
- Найти производную функции.
- Решить неравенство, полученное из производной.
- Определить интервалы, на которых производная функции положительна или отрицательна.
Если производная положительна на интервале, то функция возрастает на этом интервале. Если производная отрицательна на интервале, то функция убывает на этом интервале. Таким образом, знак производной помогает определить направление изменения функции в заданной точке.
Для удобства определения знака производной можно воспользоваться таблицей знаков. В таблице знаков указываются интервалы, на которых производная функции положительна или отрицательна, а также значения, на которых функция меняет свой знак. С помощью таблицы знаков можно точно определить поведение функции и выявить точки экстремума или точки перегиба.
Знание знака производной позволяет анализировать график функции и делать выводы о ее поведении на различных интервалах. Это важный инструмент в математике и научных исследованиях.
Таблица знаков производной

В таблице знаков производной представлены основные случаи изменения знака производной и соответствующие значения:
- Если производная положительна, то функция возрастает.
- Если производная отрицательна, то функция убывает.
- Если производная равна нулю, то функция имеет экстремум.
Также стоит отметить следующие моменты:
- Если производная меняет знак с положительного на отрицательный при переходе через точку, то функция имеет максимум в этой точке.
- Если производная меняет знак с отрицательного на положительный при переходе через точку, то функция имеет минимум в этой точке.
- Если производная не меняет знак при переходе через точку, то функция имеет горизонтальный асимптоту или точку перегиба.
Таблица знаков производной помогает определить, как функция меняется в заданной точке и где она достигает экстремумов. Это является важным инструментом при исследовании функций и нахождении их критических точек.
Вопрос-ответ:
Что такое производная числа?
Производная числа – это понятие из математического анализа, которое позволяет узнать, как изменяется функция в зависимости от изменения ее аргумента. Математически, производная числа определяется как предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю.
Как определить знак производной числа?
Знак производной числа определяется с помощью правила знакопостоянства производной. Если производная числа положительна на интервале, то функция возрастает на этом интервале. Если производная числа отрицательна на интервале, то функция убывает на этом интервале. Если же производная числа равна нулю на интервале, то функция имеет экстремум (максимум или минимум) на этом интервале.
Какова геометрическая интерпретация производной числа?
Геометрическая интерпретация производной числа заключается в том, что она определяет наклон касательной к графику функции в точке. Если производная положительна, то касательная наклонена вверх, если отрицательна – вниз, а если равна нулю – то касательная горизонтальна.
Как найти производную числа?
Для нахождения производной числа необходимо применить некоторые правила дифференцирования. Если функция задана явно, то применяются правила дифференцирования элементарных функций. Если функция задана параметрически, то используется правило дифференцирования сложной функции. Если же функция задана неявно, то применяется правило дифференцирования неявной функции.
Примеры определения знака производной
- Если производная функции положительна на интервале, то функция возрастает на этом интервале. Например, если производная функции f(x) равна 3x^2 — 2x, то она положительна на интервале (2/3, +∞), что означает, что функция возрастает на этом интервале.
- Если производная функции отрицательна на интервале, то функция убывает на этом интервале. Например, если производная функции g(x) равна -2x^3 + 5x^2 — 3x, то она отрицательна на интервале (-∞, 0), что означает, что функция убывает на этом интервале.
- Если производная функции равна нулю в точке, то функция имеет экстремум в этой точке. Например, если производная функции h(x) равна 2x^2 — 6x + 4, то она равна нулю в точках x = 1 и x = 2, что означает, что функция имеет локальный максимум в точке x = 1 и локальный минимум в точке x = 2.
Примеры определения знака производной помогают понять, как функция меняется в различных точках и интервалах. Это важный инструмент для анализа функций и решения различных задач в математике и других областях, где используется дифференциальное исчисление.




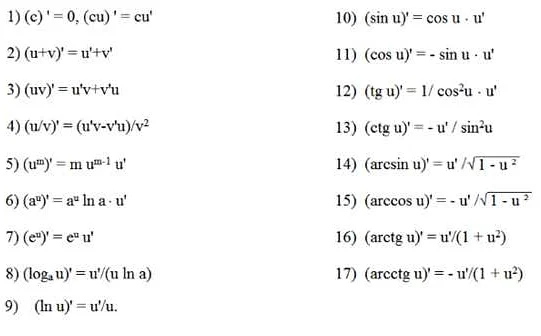

Очень интересная и полезная статья! Я всегда задавалась вопросом, что такое производная числа в математике и как можно определить ее знак. Благодаря этой статье я получила ясные и понятные объяснения. Производная числа — это скорость изменения функции в данной точке. Знак производной показывает, в каком направлении функция меняется: положительный знак означает рост функции, а отрицательный — убывание. Теперь я понимаю, как можно использовать производную для анализа функций и решения различных задач. Спасибо за полезную информацию!
Производная числа в математике – это важный концепт, позволяющий понять изменение значения функции по мере изменения ее аргумента. Знание знака производной позволяет определить поведение функции в определенной точке. Например, если производная положительна в некоторой точке, это означает, что функция возрастает в этой точке. Если производная отрицательна, то функция убывает. А если производная равна нулю, это может указывать на экстремум функции. Определение знака производной – это важный инструмент для решения многих задач в математике и ее приложениях. Например, зная знак производной функции, можно найти точки максимума и минимума функции, что имеет большое значение в оптимизации и экономике. Понимание производной и ее знака помогает также в построении графиков функций и анализе их поведения. Это позволяет предсказать, как будет изменяться значение функции в зависимости от изменения аргумента. В целом, понимание производной числа и ее знака – это неотъемлемая часть математической грамотности и является базовым инструментом для решения различных задач. Необходимо уделять должное внимание этой концепции, чтобы успешно развиваться в математике и применять ее в реальной жизни.