От какой величины зависит период колебаний математического маятника

Период колебаний математического маятника зависит от его длины и силы тяжести. Чем больше длина маятника и сила тяжести, тем больше будет период колебаний.

Математический маятник — это система, состоящая из точечной массы, подвешенной на невесомой нити или стержне. Он является одной из простейших физических моделей и используется для изучения колебательных процессов.

Период колебаний — это временной интервал, за который маятник совершает одну полную колебательную величину (например, отклонение и возвращение к положению равновесия). Период колебаний зависит от многих факторов, включая длину нити или стержня, массу маятника и силы тяжести, действующую на него.

Исследование зависимости периода колебаний математического маятника от его величины позволяет лучше понять физические законы, описывающие колебательные системы. Результаты таких исследований могут быть использованы для разработки более точных моделей и прогнозирования поведения других колебательных систем, например, маятников в механизмах или электронных часах.

Математический маятник обладает особой геометрической и физической структурой, что делает его одним из наиболее исследуемых объектов в физике. Изучение зависимости периода колебаний от его величины помогает установить закономерности и уточнить формулы, описывающие динамику колебательных систем.

В данной статье будет рассмотрена зависимость периода колебаний математического маятника от его величины и приведены основные формулы, используемые для расчетов. Также будут рассмотрены факторы, влияющие на период колебаний, и проведены эксперименты для проверки полученных результатов. Изучение этой зависимости позволит более глубоко понять физические законы и применить полученные знания в практических целях.

Зависимость периода колебаний

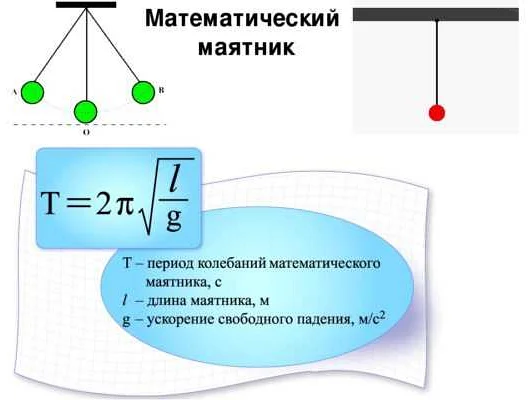
Согласно формуле для периода колебаний математического маятника:

T = 2π√(l/g)

где T — период колебаний, l — длина маятника, g — ускорение свободного падения.

Из этой формулы видно, что период колебаний обратно пропорционален квадратному корню из длины маятника и прямо пропорционален квадратному корню из ускорения свободного падения.

Таким образом, чем длиннее математический маятник, тем дольше его период колебаний. А с увеличением ускорения свободного падения период колебаний также увеличивается.

Эта зависимость позволяет установить связь между физическими свойствами маятника и его периодом колебаний, что имеет важное значение для понимания и изучения колебательных процессов в природе и технике.

Видео по теме:

Математического маятника

Период колебаний математического маятника зависит от его величины. Он определяется формулой:

T = 2π√(L/g)

где T — период колебаний, L — длина нити или стержня, g — ускорение свободного падения.

Из этой формулы видно, что период колебаний математического маятника прямо пропорционален квадратному корню из его длины. То есть, чем длиннее нить или стержень, тем больший период колебаний будет иметь маятник.

Эта зависимость может быть объяснена законом сохранения энергии. При движении маятника энергия переходит между его потенциальной и кинетической энергией. Потенциальная энергия маятника возрастает с увеличением его высоты, а кинетическая энергия возрастает с увеличением его скорости. Период колебаний маятника определяется таким образом, чтобы потенциальная и кинетическая энергии менялись с одинаковой частотой.

Изучение зависимости периода колебаний от величины математического маятника является важной задачей в физике. Эта зависимость может быть использована для измерения ускорения свободного падения и определения длины нити или стержня маятника. Также, зная период колебаний, можно получить информацию о других характеристиках системы, таких как масса маятника или сила трения.

Понятие и принцип работы

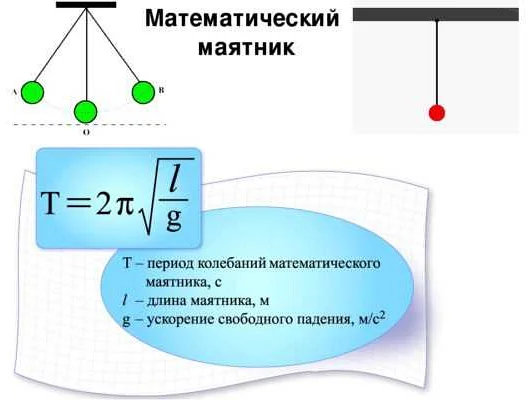
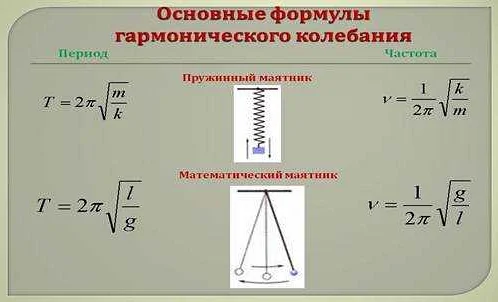
Принцип работы математического маятника основан на применении закона Гука, который утверждает, что период колебаний зависит только от длины подвеса и силы тяжести. Период колебаний – это время, за которое маятник совершает одно полное колебание от одной крайней точки до другой и обратно.

Для математического маятника период колебаний можно выразить формулой:

T = 2π√(L/g)

где T – период колебаний, L – длина подвеса маятника, g – ускорение свободного падения.

Из формулы видно, что период колебаний обратно пропорционален квадратному корню из длины подвеса и прямо пропорционален квадратному корню из ускорения свободного падения. Это означает, что при увеличении длины подвеса период колебаний увеличивается, а при увеличении ускорения свободного падения – уменьшается.

Математический маятник является одним из простейших примеров колебательного движения и находит широкое применение в различных областях науки и техники.

Вопрос-ответ:

Как зависит период колебаний математического маятника от его величины?

Период колебаний математического маятника не зависит от его величины. Он зависит только от длины подвеса и ускорения свободного падения.

Почему период колебаний математического маятника не зависит от его величины?

Период колебаний математического маятника определяется только длиной подвеса и ускорением свободного падения. Величина математического маятника не влияет на его период колебаний.

Какие факторы влияют на период колебаний математического маятника?

Период колебаний математического маятника зависит от длины подвеса и ускорения свободного падения. Длинный маятник будет иметь больший период, а краткий — меньший. Ускорение свободного падения также влияет на период: чем больше ускорение, тем меньше период.

Можно ли изменить период колебаний математического маятника путем изменения его величины?

Нет, период колебаний математического маятника нельзя изменить путем изменения его величины. Период зависит только от длины подвеса и ускорения свободного падения.

Какие законы определяют зависимость периода колебаний математического маятника от его величины?

Зависимость периода колебаний математического маятника от его величины определяется законами динамики. В частности, период зависит от длины подвеса и ускорения свободного падения, но не зависит от величины маятника.

Зависит ли период колебаний математического маятника от его массы?

Да, период колебаний математического маятника зависит от его массы. Чем больше масса маятника, тем медленнее будет происходить его колебание. Величина периода прямо пропорциональна квадратному корню из длины маятника и обратно пропорциональна квадратному корню из ускорения свободного падения.

Как величина математического маятника влияет на его период колебаний?

Величина математического маятника, выраженная в его длине, влияет на его период колебаний. Чем больше длина маятника, тем дольше будет продолжаться его колебание, и наоборот. Период колебания математического маятника прямо пропорционален квадратному корню из его длины и обратно пропорционален квадратному корню из ускорения свободного падения.

Математического маятника

Основными характеристиками математического маятника являются его длина и период колебаний. Длина маятника – это расстояние от точки подвеса до центра масс. Она влияет на период колебаний – временной интервал, за который маятник выполняет полный цикл.

Период колебаний математического маятника зависит только от его длины и ускорения свободного падения. Математическая формула, описывающая период колебаний, выглядит следующим образом:

T = 2\pi \sqrt{\frac{L}{g}}

где T – период колебаний, L – длина маятника, g – ускорение свободного падения.

Таким образом, увеличение длины маятника приводит к увеличению его периода колебаний. Это связано с тем, что более длинный маятник имеет большую массу, и, следовательно, большую инерцию, что замедляет его движение и увеличивает время одного цикла.

Математический маятник является одной из фундаментальных моделей в физике, его изучение позволяет понять основные законы колебательных процессов и применить их в различных практических областях, таких как механика, электроника и аккустика.

Формула периода колебаний

Период колебаний математического маятника зависит от его величины и может быть вычислен с использованием следующей формулы:

T = 2π√(l/g)

где:

• T — период колебаний, выраженный в секундах;
• π — математическая константа, примерно равная 3.14159;
• l — длина математического маятника, выраженная в метрах;
• g — ускорение свободного падения, выраженное в метрах в секунду в квадрате.

Таким образом, период колебаний математического маятника зависит только от его длины и ускорения свободного падения. Чем длиннее маятник, тем дольше его период колебаний. А ускорение свободного падения остается постоянным на Земле и равно примерно 9.8 метров в секунду в квадрате.

Математического маятника

Основные характеристики математического маятника — это его период колебаний и амплитуда. Период колебаний — это время, за которое маятник делает одно полное колебание вперед и назад. Амплитуда — это максимальное отклонение маятника от положения равновесия.

Период колебаний математического маятника зависит от его величины. При увеличении длины маятника, его период колебаний увеличивается, а при уменьшении длины — уменьшается. Это явление называется законом математического маятника и было открыто Галилео Галилеем в 16 веке.

Математический маятник имеет множество приложений, как в научных исследованиях, так и в повседневной жизни. Например, он используется в физических экспериментах для измерения ускорения свободного падения, в часах для поддержания точного времени и в других технических устройствах.

Изучение математического маятника помогает усвоить основы динамики и осцилляций, а также развивает навыки математического моделирования и анализа данных. Этот простой и универсальный объект позволяет в полной мере ощутить красоту физических законов и установить прямую связь между математикой и реальным миром.

Влияние величины маятника

Это связано с тем, что при увеличении величины маятника увеличивается его момент инерции. Момент инерции — это физическая величина, которая характеризует инертность тела относительно оси вращения. Чем больше момент инерции маятника, тем больше усилий требуется для его изменения состояния движения.

Согласно закону сохранения энергии, энергия маятника не изменяется во время колебаний. Поэтому, при увеличении момента инерции маятника, он будет колебаться с меньшей амплитудой, что приводит к увеличению периода колебаний.

Таким образом, величина математического маятника напрямую связана с его периодом колебаний. Большие маятники будут иметь больший период колебаний, а маленькие маятники — меньший период колебаний.

Важно отметить, что влияние величины маятника на его период колебаний является одним из факторов, который нужно учитывать при проведении экспериментов и анализе результатов.

На его период колебаний

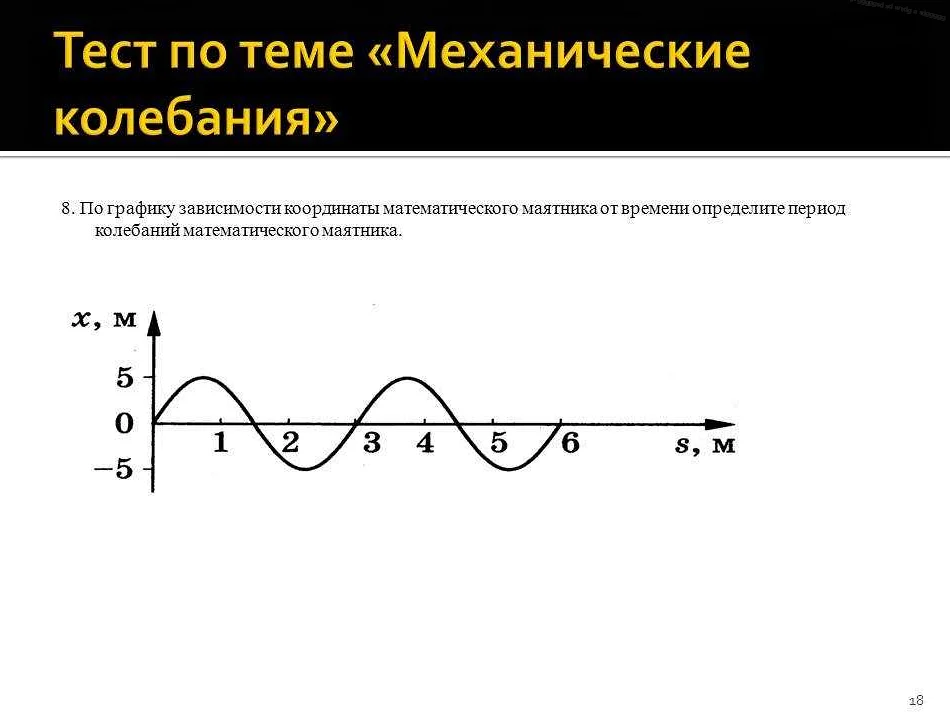
Согласно формуле для периода колебаний, период зависит от длины маятника и силы тяжести:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Из формулы видно, что период колебаний обратно пропорционален квадратному корню из длины маятника и прямо пропорционален квадратному корню из ускорения свободного падения. То есть, чем длиннее маятник, тем дольше его период колебаний, а чем сильнее сила тяжести, тем короче период.

Данная зависимость позволяет устанавливать соответствующую величину маятника для получения желаемого периода колебаний. Например, для создания маятника с более длинным периодом колебаний можно увеличить его длину.

Изучение зависимости периода колебаний от величины математического маятника имеет практическое применение в различных областях науки и техники, таких как физика, механика, астрономия и другие.

Масса маятника и период колебаний

Чем больше масса маятника, тем медленнее он будет колебаться, а период его колебаний будет увеличиваться. Это связано с законом сохранения энергии, так как энергия потенциальная маятника пропорциональна его массе.

Масса маятника также влияет на амплитуду колебаний — максимальное отклонение маятника от положения равновесия. Чем больше масса маятника, тем меньше его амплитуда колебаний.

Важно отметить, что зависимость периода колебаний от массы маятника не является линейной. Это значит, что удвоение массы маятника не приведет к удвоению периода его колебаний. Зависимость периода колебаний от массы маятника является обратной, что означает, что с увеличением массы период колебаний будет увеличиваться, но не в прямой пропорции.

Таким образом, масса математического маятника оказывает существенное влияние на его период колебаний. Изменение массы маятника может привести к изменению его периода и амплитуды колебаний, что делает массу одним из факторов, которые необходимо учитывать при исследовании и изучении математических маятников.

Зависимость и взаимосвязь

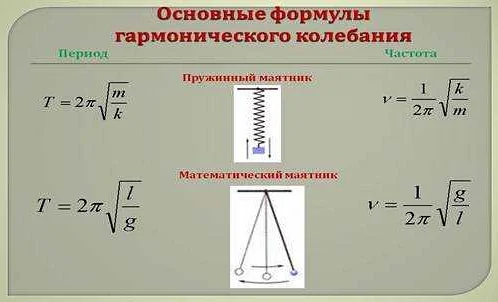
Величина маятника определяется его длиной, то есть расстоянием между точкой подвеса и центром масс маятника. Чем длиннее маятник, тем больше времени требуется для совершения полного колебания в одну сторону и обратно.

Эта зависимость можно объяснить основным физическим законом, который управляет колебаниями математического маятника — законом сохранения энергии. При колебаниях маятника его потенциальная энергия переходит в кинетическую и обратно. Чем больше потенциальная энергия на верхней точке колебания, тем больше кинетическая энергия на нижней точке и наоборот. И чем длиннее маятник, тем больше его потенциальная энергия на верхней точке, что приводит к увеличению периода колебаний.

Таким образом, зависимость периода колебаний математического маятника от его величины является неотъемлемой и объясняется основными законами физики. Изучение этой зависимости позволяет более глубоко понять и описать этот физический процесс.