Какую длину должен иметь секундный математический маятник
Содержимое
- 1 Какую длину должен иметь секундный математический маятник
- 1.1 Как выбрать длину секундного математического маятника
- 1.2 Видео по теме:
- 1.3 Формула и расчеты для определения длины маятника
- 1.4 Влияние длины маятника на его период
- 1.5 Оптимальная длина маятника для точного измерения времени
- 1.6 Зависимость длины маятника от гравитационного ускорения
- 1.7 Как выбрать длину маятника для конкретной задачи
- 1.8 Экспериментальные методы определения длины маятника
- 1.9 Как учесть воздействие ветра на длину маятника
- 1.10 Практические примеры расчета длины секундного математического маятника
- 1.11 Вопрос-ответ:
- 1.11.0.1 Какую формулу использовать для расчета длины секундного математического маятника?
- 1.11.0.2 Какое значение ускорения свободного падения нужно использовать при расчете длины секундного математического маятника?
- 1.11.0.3 Какой период колебаний нужно использовать при расчете длины секундного математического маятника?
- 1.11.0.4 Какие единицы измерения используются для длины секундного математического маятника?
- 1.11.0.5 Как можно увеличить длину секундного математического маятника?
Узнайте, какая должна быть длина секундного математического маятника для точного измерения времени и почему это значение так важно. Научитесь расчету длины маятника и понимайте его влияние на точность измерений.
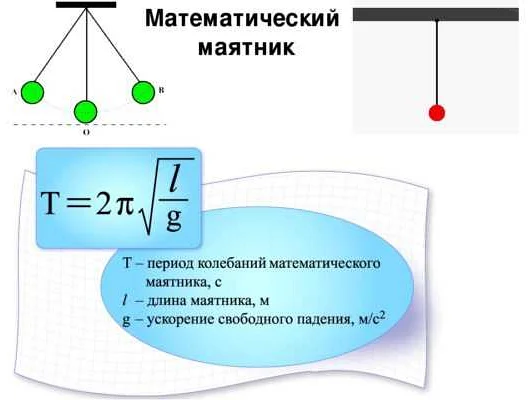
Секундный математический маятник — это физический объект, который используется для измерения времени. Он состоит из невесомой нерастяжимой нити и точечной массы, которая считается материальной точкой. При движении маятника, его период зависит от его длины, которая, в свою очередь, может быть рассчитана по формуле.
Формула для расчета длины секундного математического маятника выглядит следующим образом:
L = g * T^2 / (4 * π^2)
Где L — длина маятника, g — ускорение свободного падения, T — период колебаний маятника, π — математическая константа, равная примерно 3.14.
Расчет длины секундного математического маятника является важным для обеспечения точности измерений времени. Зная значение периода и ускорения свободного падения, можно определить оптимальную длину маятника, при которой его колебания будут иметь период в одну секунду.
Как выбрать длину секундного математического маятника
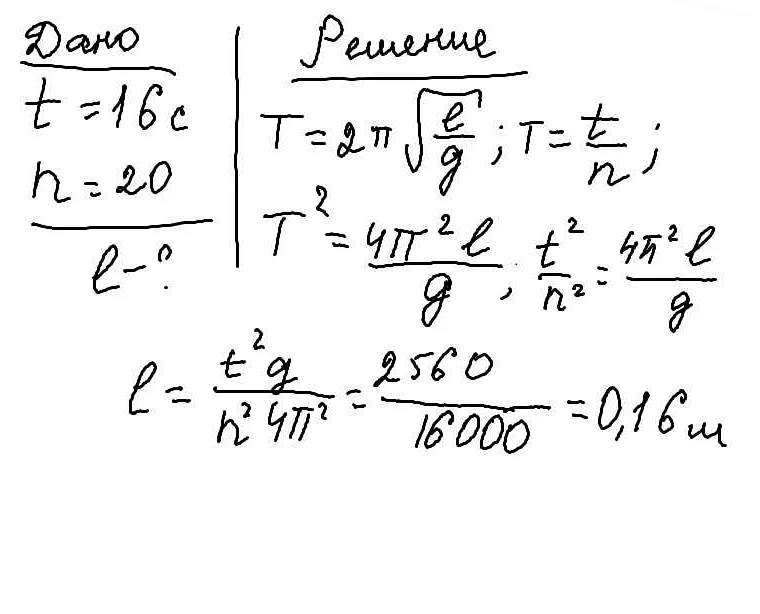
Для выбора длины секундного математического маятника можно использовать следующую формулу:
- Определите значение ускорения свободного падения (g) в месте, где будет расположен маятник. Обычно это значение равно примерно 9,8 м/с².
- Определите желаемый период колебаний (T) в секундах. Например, для секундного маятника значение периода равно 1 секунде.
- Используя формулу T = 2π√(l/g), где l — длина маятника, решите ее относительно l.
- Подставьте значения g и T в формулу и рассчитайте длину маятника.
Например, если ускорение свободного падения равно 9,8 м/с² и желаемый период колебаний равен 1 секунде, то длина маятника будет:
l = (T/2π)² * g = (1/2π)² * 9,8 ≈ 0,249 метра.
Таким образом, для выбора длины секундного математического маятника необходимо знать значение ускорения свободного падения в данном месте и желаемый период колебаний. Используя соответствующую формулу, можно рассчитать оптимальную длину маятника, чтобы он выполнял одно полное колебание за одну секунду.
Видео по теме:
Формула и расчеты для определения длины маятника
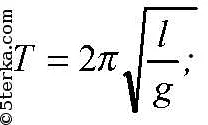
Длина секундного математического маятника можно определить с использованием простой формулы. Данная формула позволяет вычислить длину маятника на основе периода его колебаний.
Формула для определения длины секундного математического маятника выглядит следующим образом:
| Длина маятника (L) | = | g | * | (T | / | 2π) | 2 |
Где:
- L — длина маятника;
- g — ускорение свободного падения (около 9,8 м/с2);
- T — период колебаний маятника;
- π — математическая константа, примерно равная 3,14.
Для расчета длины маятника необходимо знать значение ускорения свободного падения и период его колебаний. Подставив эти значения в формулу, можно получить необходимую длину маятника.
Влияние длины маятника на его период
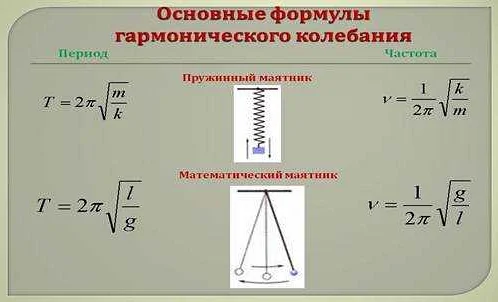
Формула для расчета периода математического маятника связывает его длину и ускорение свободного падения:
T = 2π * √(L / g),
где T — период маятника, L — его длина, g — ускорение свободного падения.
Из формулы видно, что период маятника прямо пропорционален квадратному корню из его длины. То есть, с увеличением длины маятника, его период также увеличивается.
Данная зависимость может быть объяснена следующим образом: при увеличении длины маятника, увеличивается путь, который он проходит при каждом колебании. Более длинный маятник требует большего времени для прохождения этого пути, что и приводит к увеличению его периода.
Таким образом, длина маятника оказывает прямое влияние на его период. При решении задач по расчету периода математического маятника, необходимо учитывать данную зависимость.
Оптимальная длина маятника для точного измерения времени
Для точного измерения времени с использованием математического маятника, необходимо выбрать оптимальную длину этого маятника. Оптимальная длина маятника зависит от ускорения свободного падения на данной местности и предназначена для обеспечения наиболее точного измерения времени.
Формула для расчета оптимальной длины секундного математического маятника выглядит следующим образом:
L = g * T^2 / (4 * π^2)
Где:
- L — длина маятника
- g — ускорение свободного падения (приближенное значение 9,8 м/с^2 на поверхности Земли)
- T — период колебаний маятника (в данном случае, секунды)
- π — математическая константа, приблизительно равная 3,14159
Математический маятник с такой оптимальной длиной будет совершать одно колебание за одну секунду. Таким образом, при условии точной измерительной системы, такой маятник может использоваться для точного измерения времени.
Однако, следует учесть, что формула представляет идеализированную модель маятника и не учитывает влияние воздушного сопротивления, трения и других факторов. Поэтому в реальных условиях могут потребоваться дополнительные корректировки.
Зависимость длины маятника от гравитационного ускорения
Формула, которая описывает зависимость длины математического маятника от гравитационного ускорения, называется формулой периода колебаний:
T = 2π√(l/g)
Где T — период колебаний, l — длина маятника, g — гравитационное ускорение.
Из этой формулы видно, что длина маятника обратно пропорциональна квадратному корню из гравитационного ускорения. То есть, увеличение гравитационного ускорения приведет к уменьшению длины маятника, а уменьшение гравитационного ускорения — к увеличению его длины.
Таким образом, длина секундного математического маятника будет зависеть от величины гравитационного ускорения, причем эта зависимость будет обратно пропорциональной.
Как выбрать длину маятника для конкретной задачи
Длина математического маятника играет важную роль в его движении и определяет его период колебаний. Для различных задач может потребоваться выбрать оптимальную длину маятника, чтобы достичь желаемого результата.
Формула для расчета периода колебаний математического маятника имеет вид:
T = 2π√(L/g)
где:
- T — период колебаний маятника (в секундах)
- L — длина маятника (в метрах)
- g — ускорение свободного падения (приближенное значение 9,8 м/с²)
Исходя из этой формулы, можно сделать вывод, что длина маятника напрямую влияет на его период колебаний. Чем длиннее маятник, тем дольше будет продолжаться каждое колебание, и наоборот.
При выборе длины маятника для конкретной задачи следует учитывать желаемый период колебаний. Если требуется, чтобы маятник колебался с определенной частотой, то необходимо рассчитать необходимую длину маятника, используя формулу выше.
Если задача заключается в сравнении различных длин маятников, то можно провести эксперименты с разными длинами и измерить периоды колебаний для каждого маятника. Затем построить график зависимости периода от длины маятника и анализировать полученные данные.
Короткие маятники имеют более высокую частоту колебаний, что может быть полезным для определенных задач, например, для измерения времени с высокой точностью. Длинные маятники имеют более низкую частоту колебаний и могут использоваться для изучения длительных периодических процессов.
Важно отметить, что в реальности существует ряд факторов, которые могут влиять на движение маятника и его период колебаний, такие как сопротивление воздуха, масса маятника и т.д. Поэтому при выборе длины маятника необходимо учитывать эти факторы и применять соответствующие поправки к расчетам.
Экспериментальные методы определения длины маятника
- Метод одного периода колебаний. В этом методе необходимо засекать время, за которое маятник совершает одно полное колебание. Затем по формуле Т = 2π√(L/g), где Т — период колебаний, L — длина маятника, g — ускорение свободного падения, можно определить длину маятника.
- Метод сравнения периодов. В этом методе сначала определяют длину одного маятника, а затем сравнивают период колебаний секундного маятника с периодом эталонного маятника. По сравнению периодов можно определить отношение длин маятников и, таким образом, найти длину секундного маятника.
- Метод разных длин. В этом методе используется несколько маятников разных длин. Определяется период колебаний каждого маятника, а затем строится график зависимости периода от квадратного корня из длины маятника. По графику можно найти длину секундного маятника.
- Метод математического маятника с грузами. В этом методе к секундному маятнику прикрепляются грузы разной массы. Определяется период колебаний для каждой массы груза, а затем используется формула для математического маятника с грузами, позволяющая определить длину маятника.
Каждый из этих экспериментальных методов имеет свои преимущества и ограничения. Выбор метода зависит от условий и целей исследования. Правильное определение длины маятника позволяет получить точные результаты и использовать эти данные для решения различных задач в физике и других науках.
Как учесть воздействие ветра на длину маятника
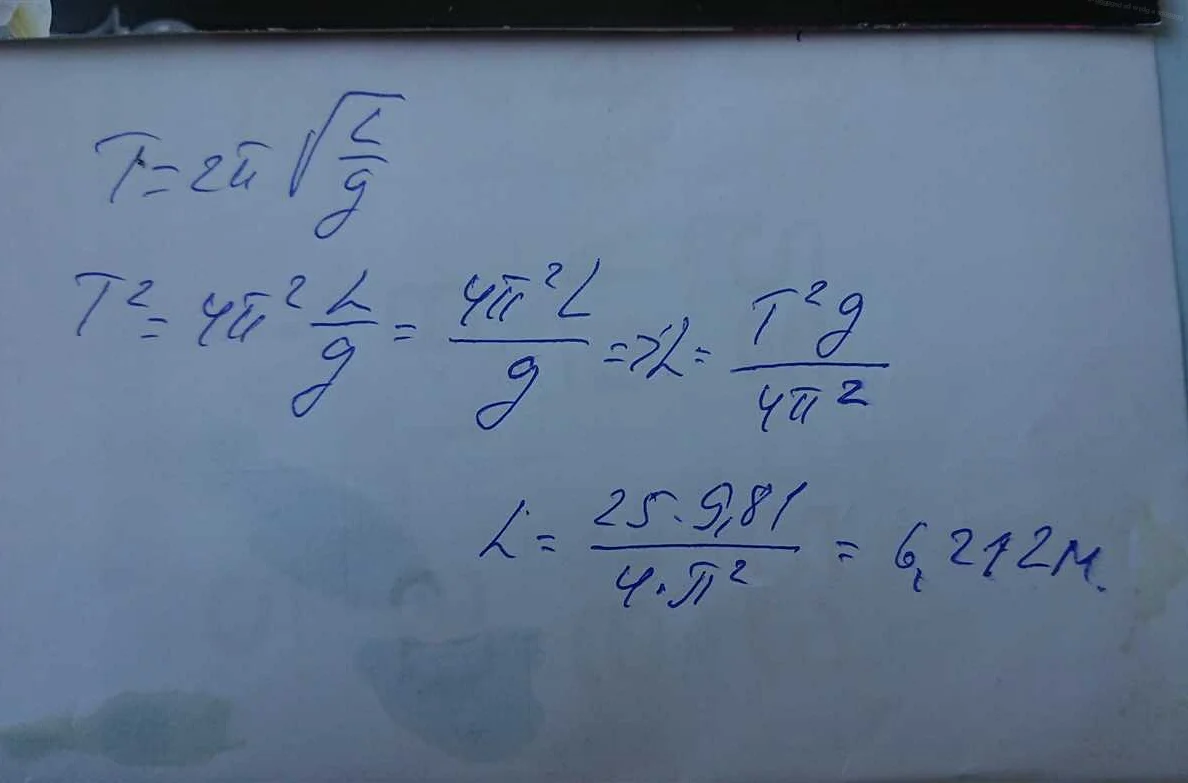
При расчете длины секундного математического маятника, необходимо учесть воздействие ветра, так как оно может оказывать значительное влияние на его колебания. Ветер создает силу сопротивления, которая может изменять период колебаний маятника и, следовательно, его длину.
Для учета воздействия ветра на маятник необходимо воспользоваться специальными формулами и расчетами. Одной из таких формул является формула, которая позволяет определить допустимую максимальную скорость ветра при заданной длине маятника.
Эта формула основана на балансе сил, действующих на маятник. Воздействие ветра создает силу сопротивления, которая направлена противоположно движению маятника. Для того, чтобы маятник продолжал свои колебания, сила сопротивления ветра должна быть меньше силы тяжести, действующей на маятник.
Для определения допустимой максимальной скорости ветра при заданной длине маятника, можно воспользоваться следующей формулой:
Максимальная скорость ветра = (длина маятника * ускорение свободного падения) / (2 * pi)
В этой формуле длина маятника указывается в метрах, а ускорение свободного падения принимается равным примерно 9,8 м/с^2. Результатом расчета будет максимальная скорость ветра в м/с, при которой маятник будет продолжать свои колебания.
Таким образом, учет воздействия ветра на длину секундного математического маятника является важным аспектом при его расчете. Формула, описанная выше, позволяет определить допустимую максимальную скорость ветра при заданной длине маятника и ускорении свободного падения.
Практические примеры расчета длины секундного математического маятника

Для расчета длины секундного математического маятника можно использовать следующую формулу:
L = g * T^2 / (4 * π^2)
где:
- L — длина маятника (в метрах)
- g — ускорение свободного падения (приближенное значение 9,8 м/с^2)
- T — период колебаний маятника (в секундах)
- π — математическая константа, приближенное значение 3,14159
Давайте рассмотрим несколько практических примеров расчета длины секундного математического маятника:
Пример 1:
Пусть период колебаний маятника равен 2 секунды. Подставим данное значение в формулу:
L = 9,8 * (2^2) / (4 * 3,14159^2)
L = 9,8 * 4 / (4 * 9,8696)
L = 0,98 метра
Пример 2:
Пусть период колебаний маятника равен 1,5 секунды. Подставим данное значение в формулу:
L = 9,8 * (1,5^2) / (4 * 3,14159^2)
L = 9,8 * 2,25 / (4 * 9,8696)
L = 0,56 метра
Пример 3:
Пусть период колебаний маятника равен 3,5 секунды. Подставим данное значение в формулу:
L = 9,8 * (3,5^2) / (4 * 3,14159^2)
L = 9,8 * 12,25 / (4 * 9,8696)
L = 3,06 метра
Таким образом, для различных значений периода колебаний маятника можно рассчитать соответствующую длину секундного математического маятника с помощью данной формулы.
Вопрос-ответ:
Какую формулу использовать для расчета длины секундного математического маятника?
Формула для расчета длины секундного математического маятника имеет вид: L = gT^2 / (4π^2), где L — длина маятника, g — ускорение свободного падения, а T — период колебаний.
Какое значение ускорения свободного падения нужно использовать при расчете длины секундного математического маятника?
Для расчета длины секундного математического маятника необходимо использовать значение ускорения свободного падения на поверхности Земли, которое обычно равно примерно 9.8 м/с^2.
Какой период колебаний нужно использовать при расчете длины секундного математического маятника?
Для расчета длины секундного математического маятника необходимо использовать период колебаний, то есть время, за которое маятник выполняет один полный цикл колебаний. В случае секундного маятника, период колебаний равен 1 секунде.
Какие единицы измерения используются для длины секундного математического маятника?
Длина секундного математического маятника обычно измеряется в метрах (м).
Как можно увеличить длину секундного математического маятника?
Длину секундного математического маятника можно увеличить путем увеличения значения ускорения свободного падения или увеличения периода колебаний. Также можно увеличить длину физического маятника, на котором будет закреплен секундный маятник.
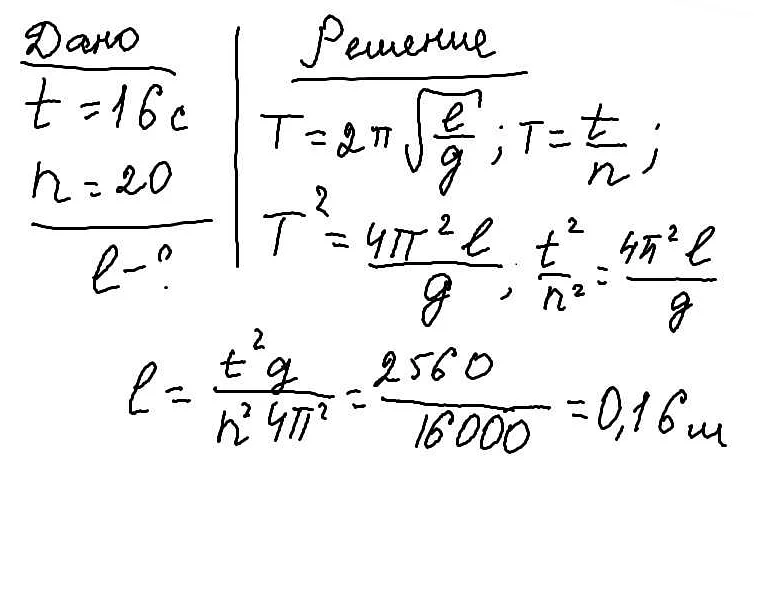


Статья очень познавательная и интересная. Я всегда задавался вопросом, как рассчитывается оптимальная длина секундного математического маятника. И вот, наконец, я нашел ответ! Формула и расчеты, описанные в статье, позволяют определить длину маятника, при которой его период будет равен одной секунде. Как оказалось, эта длина зависит от ускорения свободного падения на Земле. Теперь я знаю, что для моего маятника я должен выбрать такую длину, чтобы период его колебаний составлял ровно одну секунду. Такой маятник будет идеальным для моих экспериментов с измерением времени. Приятно осознавать, что я теперь знаю не только формулу и расчеты, но и понимаю, каким образом они работают. Статья дала мне ценные знания и позволила лучше разобраться в этой интересной и важной теме. Спасибо за полезную информацию!