Какой нумерацией пользуются школьники на уроках математики

Узнайте, какую нумерацию используют школьники при решении задач на уроках математики. Уроки по математике для школьников часто требуют использования определенной системы нумерации. Узнайте, как правильно нумеровать задачи и решения, чтобы добиться правильных ответов и успешного усвоения материала.

Система нумерации – это способ записи и представления чисел. Она является основой всех математических операций и позволяет нам работать с числами любого размера. В школе дети изучают несколько систем нумерации, но основную роль играет десятичная система.

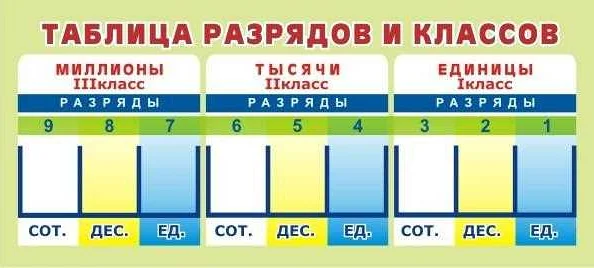
Десятичная система нумерации основана на использовании десяти цифр: от 0 до 9. Цифры в этой системе имеют разряды, которые местами расположены справа налево. Каждый разряд представляет собой степень числа 10. Например, число 1234 можно разложить на разряды следующим образом: 1*1000 + 2*100 + 3*10 + 4*1.

Десятичная система нумерации широко используется в повседневной жизни и во многих областях, включая финансы, науку и технологии. Однако, на уроках математики школьники также знакомятся с другими системами нумерации, такими как двоичная, восьмеричная и шестнадцатеричная.

Двоичная система нумерации основана на использовании двух цифр: 0 и 1. Она широко применяется в компьютерах и цифровой технике, так как любая информация может быть представлена в виде двоичного кода.

Восьмеричная система нумерации основана на использовании восьми цифр: от 0 до 7. Восьмеричные числа используются в некоторых областях, таких как системы счисления и программирование.

Шестнадцатеричная система нумерации основана на использовании шестнадцати цифр: от 0 до 9 и от A до F. Она широко применяется в программировании, особенно для представления цветов, адресов памяти и других значений.

Изучение разных систем нумерации помогает школьникам развивать логическое мышление и понимание базовых математических концепций. Это также помогает им лучше понимать и использовать компьютерные технологии, которые являются неотъемлемой частью современного мира.

Системы нумерации в математике: учебные примеры для школьников

На уроках математики школьники изучают различные системы нумерации, которые используются для представления чисел. Это важная тема, так как позволяет понять, как работает числовой ряд и как можно представить число в различных форматах.

Одной из наиболее распространенных систем нумерации является десятичная система. В ней используются десять символов (цифр) – от 0 до 9. Число представляется в виде комбинации этих символов, где каждая цифра обозначает определенное количество единиц, десятков, сотен и так далее в зависимости от своего разряда. Например, число 1234 в десятичной системе представляет собой 1 тысячу, 2 сотни, 3 десятка и 4 единицы.

Еще одной интересной системой нумерации является двоичная система. В ней используются всего две цифры – 0 и 1. Число представляется в виде комбинации этих двух символов, где каждая цифра обозначает определенное количество единиц, двоек, четверок и так далее в зависимости от своего разряда. Например, число 1011 в двоичной системе представляет собой 1 восьмерку, 0 четверки, 1 двойку и 1 единицу.

Кроме десятичной и двоичной систем нумерации, существуют еще многие другие, такие как восьмеричная, шестнадцатеричная и др. Все они имеют свои особенности и применяются в различных областях науки и техники.

Учебные примеры помогают школьникам лучше понять, как работают различные системы нумерации. Например, можно предложить задания на перевод чисел из одной системы в другую, на сложение или вычитание чисел в разных системах и т. д. Это помогает ученикам закрепить полученные знания и развить навыки работы с числовыми системами.

Система нумерацииОснованиеПример числа

Десятичная	10	1234
Двоичная	2	1011
Восьмеричная	8	567
Шестнадцатеричная	16	ABCD

Изучение систем нумерации в математике помогает школьникам развить логическое мышление, абстрактное мышление и усилить навыки работы с числами. Это важные навыки, которые пригодятся им не только в математике, но и в других областях жизни.

Видео по теме:

Десятичная система счисления: основные принципы и примеры

Основной принцип десятичной системы счисления заключается в том, что каждая цифра в числе представляет определенное количество единиц, десятков, сотен, тысяч и так далее. Например, число 1234 можно разложить на 1 тысячу, 2 сотни, 3 десятка и 4 единицы.

Для более наглядного представления десятичной системы счисления позиции чисел обычно обозначают с помощью индексов. Например, число 1234 можно записать как 1*103 + 2*102 + 3*101 + 4*100.

Десятичная система счисления особенно удобна для работы с большими числами и десятичными дробями. Например, число π можно представить в десятичной системе счисления с большим количеством знаков после запятой: 3.14159265358979323846.

В школьных уроках математики школьники часто практикуют работу с десятичной системой счисления, решая задачи, выполняя арифметические операции и переводя числа из одной системы счисления в другую.

Примеры:

1. Перевод числа из десятичной системы в двоичную систему счисления: число 10 в двоичной системе равно 1010.

2. Выполнение арифметических операций: 10 + 5 = 15.

3. Перевод числа из десятичной системы в шестнадцатеричную систему счисления: число 15 в шестнадцатеричной системе равно F.

Понимание десятичной системы счисления является важным базовым навыком для школьников и помогает им развивать логическое мышление и умение решать математические задачи.

Двоичная система счисления: примеры использования в информатике и электронике

В информатике двоичная система счисления широко используется для представления и обработки данных в компьютерах. Вся информация в компьютере хранится и обрабатывается в виде двоичных чисел. Например, цифровые сигналы внутри компьютера представляются двоичными числами: напряжение высокого уровня соответствует единице (1), а напряжение низкого уровня — нулю (0).

Двоичная система счисления также широко используется в электронике. Например, в цифровых схемах и микросхемах, двоичные числа используются для представления логических состояний: высокий уровень напряжения соответствует логической единице (1), а низкий уровень — логическому нулю (0). Это позволяет создавать сложные логические схемы и проектировать цифровые устройства.

Двоичная система счисления также используется для представления цветов в графике и изображении. Например, в цветовой модели RGB, каждый цвет представляется комбинацией трех двоичных чисел, представляющих интенсивность красного (R), зеленого (G) и синего (B) цветов. Каждое из чисел может принимать значения от 0 до 255, что соответствует комбинации 8 бит.

В области алгоритмов и структур данных также широко используется двоичная система счисления. Например, двоичное дерево — это структура данных, состоящая из узлов, в которой каждый узел имеет максимум два потомка. Двоичные поисковые деревья используются для эффективного поиска и сортировки данных.

Десятичное числоДвоичное число

0	0000
1	0001
2	0010
3	0011
4	0100
5	0101
6	0110
7	0111
8	1000
9	1001

Двоичная система счисления является основой для многих аспектов информатики и электроники. Понимание и умение работать с двоичными числами позволяет эффективно решать задачи в этих областях.

Восьмеричная система счисления: преимущества и ограничения

Преимуществом восьмеричной системы счисления является ее компактность. Поскольку восьмеричная система имеет меньше цифр, чем десятичная система, числа в ней занимают меньше места. Это может быть полезно при выполнении математических операций, особенно с большими числами.

Еще одним преимуществом восьмеричной системы счисления является ее связь с двоичной системой счисления. Восьмеричные числа можно представить в виде последовательности троек двоичных цифр, что упрощает перевод чисел из одной системы в другую.

Однако восьмеричная система счисления имеет и некоторые ограничения. Во-первых, поскольку она имеет меньше цифр, чем десятичная система, она не может представлять некоторые числа, такие как 8 и 9. Во-вторых, использование восьмеричной системы не всегда удобно для людей, привыкших к десятичной системе счисления.

Тем не менее, восьмеричная система счисления имеет свои преимущества и может быть полезной для решения определенных математических задач. Поэтому школьники изучают ее на уроках математики вместе с другими системами счисления, такими как двоичная и шестнадцатеричная.

Шестнадцатеричная система счисления: использование в программировании

Шестнадцатеричная система счисления часто применяется для представления чисел в компьютерах, так как она позволяет компактно записывать большие числа. В программировании шестнадцатеричные числа обозначаются с помощью префикса «0x». Например, число 255 записывается как 0xFF.

Шестнадцатеричная система счисления также используется для представления цветов в компьютерной графике. Каждый цвет представляется тройкой шестнадцатеричных чисел, где каждое число описывает интенсивность красного, зеленого и синего цветов соответственно. Например, #FF0000 обозначает красный цвет, а #00FF00 обозначает зеленый цвет.

Кроме того, шестнадцатеричная система счисления используется для представления адресов памяти в компьютерах. Каждая ячейка памяти имеет уникальный адрес, который обычно записывается в шестнадцатеричной системе счисления для удобства программистов.

Использование шестнадцатеричной системы счисления в программировании позволяет более эффективно работать с большими числами, представлять цвета и адреса памяти. Понимание этой системы счисления является важным навыком для программистов и помогает им эффективно решать задачи в различных областях программирования.

Римская система счисления: особенности и примеры применения

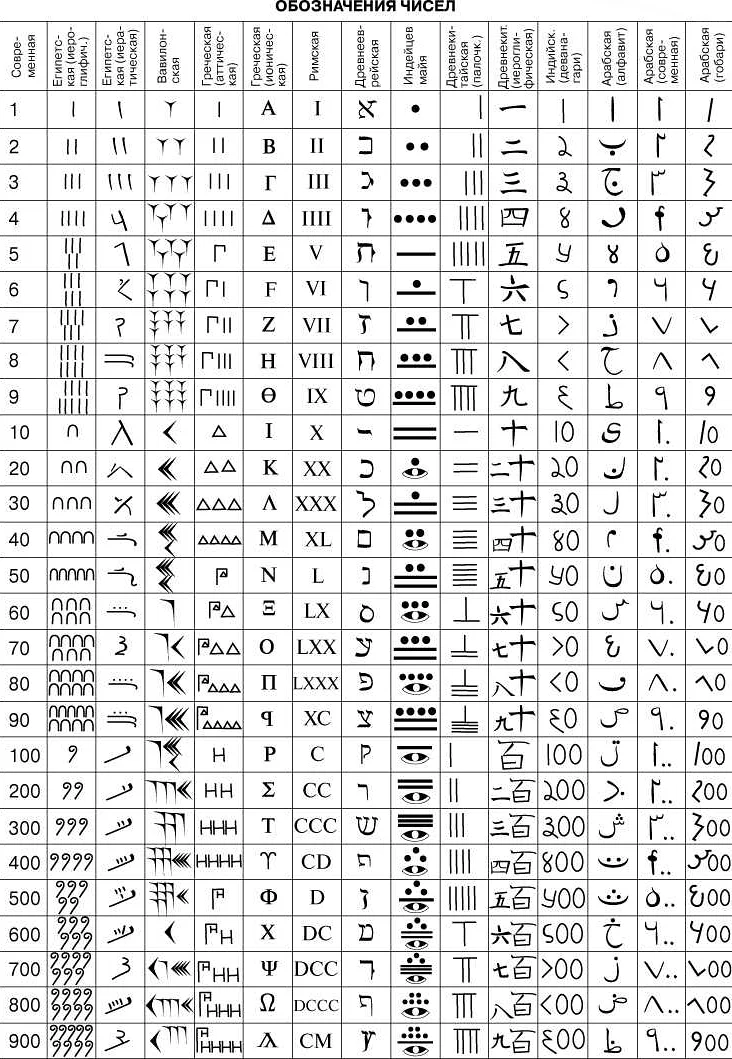
В римской системе счисления используются следующие символы:

I – 1

V – 5

X – 10

L – 50

C – 100

D – 500

M – 1000

Особенностью римской системы счисления является то, что числа записываются слитно, без использования пробелов или других разделителей. Однако существуют некоторые правила, которые необходимо соблюдать при записи чисел:

Правило 1: Если меньшая цифра стоит перед большей, то их значения складываются. Например, IV – это 4 (1 + 5).

Правило 2: Если меньшая цифра стоит после большей, то значение меньшей вычитается из значения большей. Например, IX – это 9 (10 — 1).

Правило 3: Три и более одинаковых цифры не могут идти подряд. Вместо этого используется вычитание. Например, 40 записывается как XL (50 — 10), а 900 – как CM (1000 — 100).

Римская система счисления до сих пор используется в некоторых областях, таких как нумизматика, история и культурология. Она является частью исторического наследия Римской империи и позволяет нам лучше понять историю и культуру этой древней цивилизации.

Примеры применения римской системы счисления:

II – 2

VIII – 8

XII – 12

XXV – 25

XLVIII – 48

LXIV – 64

XC – 90

CXXX – 130

CD – 400

DCCXLV – 745

CMXCIX – 999

MCMXCVIII – 1998

Ненормальные системы счисления: экзотические примеры использования

На уроках математики школьники обычно изучают десятичную систему счисления, которая основана на числе 10 и использует десять цифр от 0 до 9. Однако, существуют и другие системы счисления, которые отличаются от привычной нам десятичной системы.

Одной из ненормальных систем счисления является двоичная система, которая использует только две цифры — 0 и 1. Эта система широко применяется в компьютерах и информационных технологиях, где каждая цифра представляет собой один бит информации.

Еще одной интересной ненормальной системой счисления является восьмеричная система, которая использует восемь цифр от 0 до 7. Восьмеричная система широко применяется в программировании, так как каждая цифра в этой системе соответствует трем битам информации.

Также существует шестнадцатеричная система счисления, которая использует шестнадцать цифр от 0 до 9 и от A до F. Шестнадцатеричная система часто используется в программировании и компьютерной технике, так как позволяет компактно представлять большие числа.

Интересным примером использования ненормальных систем счисления является система счисления по основанию Фибоначчи. В этой системе используются только две цифры — 1 и 2, где каждая последующая цифра является суммой двух предыдущих. Например, число 3 в этой системе представляется как 11, а число 5 — как 111.

Ненормальные системы счисления представляют интерес не только для математиков, но и для разработчиков программного обеспечения, которые используют их для эффективного представления и обработки данных. Изучение и использование экзотических систем счисления позволяет расширить представление о числах и решать задачи, которые не могут быть решены с помощью привычных систем счисления.

Системы счисления в других культурах: интересные факты и сравнение с десятичной

Система счисления, которую мы используем в повседневной жизни, называется десятичной. Она основана на числе 10 и включает десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Такая система считается наиболее удобной для работы с числами, однако оказывается, что в разных культурах существуют и другие системы счисления, которые тоже имеют свои интересные особенности.

Один из самых известных примеров — это двоичная система счисления. Она использует всего две цифры — 0 и 1. В компьютерах и электронике двоичная система широко применяется для представления информации и выполнения операций. Как и в десятичной системе, двоичные числа могут иметь разряды, но каждый разряд в двоичной системе имеет вес, равный степени двойки.

Также существуют системы счисления с большим основанием, например, десятичная система (основание 12) и шестнадцатеричная система (основание 16). В десятичной системе вместо десяти цифр используются двенадцать: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Шестнадцатеричная система имеет цифры от 0 до 9, а затем использует буквы от A до F для обозначения чисел от 10 до 15.

Интересно, что в некоторых культурах существуют системы счисления с другими основаниями. Например, в системе счисления Майя основание равно 20, а в системе счисления в пределах группы Эвенков основание равно 5. Также существуют системы счисления с основанием 60 и 64, которые использовались в астрономии и времени в древности.

Сравнивая различные системы счисления, можно заметить, что они имеют разную степень сложности и применимости в разных областях. Десятичная система обычно считается наиболее удобной для повседневного использования и простой в понимании. Однако, в некоторых областях, таких как компьютерная наука или астрономия, более специализированные системы счисления могут быть более эффективными и удобными в использовании.

Вопрос-ответ:

Какую систему нумерации используют школьники на уроках математики?

Школьники на уроках математики используют десятичную систему нумерации, которая основана на числе 10.

Почему школьники используют именно десятичную систему нумерации?

Десятичная система нумерации выбрана для использования в школьном курсе математики, потому что она является наиболее распространенной и понятной для большинства людей. В этой системе используются цифры от 0 до 9, и числа записываются с помощью позиционного обозначения.

Как работает позиционное обозначение чисел в десятичной системе нумерации?

Позиционное обозначение чисел в десятичной системе нумерации означает, что значение каждой цифры в числе зависит от ее позиции. Например, в числе 135, цифра 5 находится в позиции единиц, цифра 3 — в позиции десятков, а цифра 1 — в позиции сотен. Таким образом, число 135 можно разложить на сумму 100 + 30 + 5.

Какие еще системы нумерации могут существовать, помимо десятичной?

Помимо десятичной системы нумерации, существуют и другие системы. Например, бинарная система основана на числе 2 и используется в компьютерах. Также есть восьмеричная система (основана на числе 8) и шестнадцатеричная система (основана на числе 16), которые также находят применение в информатике.

Почему школьники изучают другие системы нумерации, помимо десятичной?

Обучение другим системам нумерации помогает школьникам развить абстрактное мышление и понять основные принципы работы числовых систем. Это также может быть полезно при изучении информатики и программирования, где другие системы нумерации используются для представления и обработки данных.

Какую систему нумерации используют школьники на уроках математики?

Школьники на уроках математики обычно используют десятичную систему нумерации.