Системы счисления в математике какие бывают

В математике существуют различные системы счисления, такие как десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая из них имеет свои особенности и применяется в различных областях, включая информатику, электронику и программирование. Узнайте больше о различных системах счисления и их использовании.

Математика – это универсальный язык, с помощью которого мы описываем и изучаем мир. Одним из важных инструментов в этой науке является система счисления. Все числа, с которыми мы работаем, представлены в определенной системе счисления, которая определяет правила записи и взаимосвязь цифр и чисел.

Существует несколько видов систем счисления, но наиболее распространены десятичная, двоичная и шестнадцатеричная. Десятичная система счисления основана на числе 10 и использует 10 различных цифр от 0 до 9. Она широко применяется в повседневной жизни, так как мы привыкли к ней и легко можем работать с десятичными числами.

Двоичная система счисления основана на числе 2 и использует только две цифры – 0 и 1. Она широко применяется в компьютерах и электронике, так как электричество легко выражается двоичными числами. Шестнадцатеричная система счисления основана на числе 16 и использует 16 различных цифр – от 0 до 9 и от A до F. Она часто используется в программировании, так как удобна для записи и работы с большими числами.

Системы счисления являются неотъемлемой частью математики и имеют свои особенности. Знание различных систем счисления позволяет нам более полно и глубоко понять мир чисел и их взаимосвязь. Они помогают нам решать математические задачи и разрабатывать новые технологии. Поэтому изучение систем счисления является важным этапом обучения математике.

Десятичная система счисления

Каждая позиция в числе в десятичной системе имеет вес, равный степени десяти. Например, число 1234 в десятичной системе можно разложить следующим образом: 1 * 10^3 + 2 * 10^2 + 3 * 10^1 + 4 * 10^0. Это означает, что первая цифра числа (1) умножается на 10 в третьей степени (1000), вторая цифра (2) умножается на 10 во второй степени (100), третья цифра (3) умножается на 10 в первой степени (10), и четвертая цифра (4) умножается на 10 в нулевой степени (1).

Десятичная система счисления является основной системой счисления в большинстве стран мира. Она широко используется в торговле, финансах, инженерии, науке и других областях. Десятичная система обладает преимуществом простоты использования и понимания, поскольку мы привыкли к этой системе с детства.

Однако десятичная система счисления не является единственной системой счисления. В математике также используются другие системы счисления, такие как двоичная (система с основанием 2), восьмеричная (с основанием 8) и шестнадцатеричная (с основанием 16) системы счисления. Каждая система счисления имеет свои особенности и используется в разных областях.

Видео по теме:

Бинарная система счисления

В бинарной системе каждая цифра называется битом (binary digit). Бит может принимать только два значения: 0 или 1. Последовательность битов в бинарной системе образует двоичное число.

Бинарная система счисления используется для представления информации в компьютерах. В компьютерах все данные хранятся и обрабатываются в виде двоичных чисел. Каждый бит в компьютере представляет один из двух возможных состояний: выключено (0) или включено (1).

Перевод чисел из десятичной системы счисления в бинарную производится путем деления числа на 2 и записи остатков от деления. Для обратного перевода из бинарной системы в десятичную используется формула, основанная на степенях числа 2.

Бинарная система счисления имеет важное значение в компьютерных науках и электронике. Она позволяет эффективно хранить, обрабатывать и передавать информацию в цифровой форме.

Восьмеричная система счисления

Аналогично двоичной и десятичной системам, восьмеричная система использует разряды для представления чисел. Каждый разряд в восьмеричной системе имеет вес, равный степени числа 8. Например, число 247 в восьмеричной системе можно представить как 3*8^2 + 7*8^1 + 7*8^0.

Восьмеричная система счисления часто используется в компьютерных системах и программировании, так как она удобна при работе с битами и байтами информации. Восьмеричные числа часто используются для представления множества флагов и состояний в различных системах.

Для преобразования чисел из восьмеричной системы в десятичную или наоборот существуют специальные алгоритмы. Они позволяют выполнить операции сложения, вычитания, умножения и деления с числами в восьмеричной системе.

Восьмеричная система счисления имеет свои преимущества и недостатки по сравнению с другими системами счисления. Она более компактна, чем двоичная система, но уступает десятичной системе по точности представления чисел. Восьмеричная система также менее распространена и используется в основном в специальных областях, связанных с компьютерами и информатикой.

Шестнадцатеричная система счисления

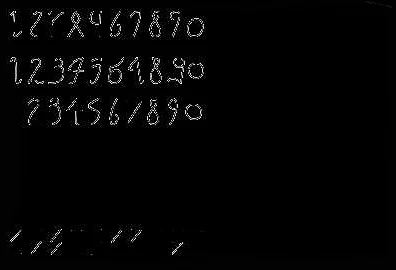
В шестнадцатеричной системе счисления цифры 0-9 представляют значения от 0 до 9, а символы A-F представляют значения от 10 до 15. Например, число 10 в шестнадцатеричной системе счисления эквивалентно числу 16 в десятичной системе счисления, а число FF эквивалентно числу 255.

Эта система счисления широко используется в компьютерных науках, а также в программировании. Она позволяет удобно представлять и работать с большими числами и позволяет сократить количество символов, требуемых для записи чисел.

Шестнадцатеричная система счисления также часто используется для представления цветов в графике и веб-дизайне. Каждый цвет представляется комбинацией трех шестнадцатеричных чисел, представляющих интенсивность красного (R), зеленого (G) и синего (B) оттенков.

Для перевода чисел из шестнадцатеричной системы счисления в десятичную можно использовать аналогичные методы, как для других систем счисления. Цифры умножаются на соответствующую степень числа 16 и складываются.

Шестнадцатеричная система счисления является важным инструментом, который помогает в решении различных математических задач и нахождении оптимальных решений в компьютерных науках и программировании.

Римская система счисления

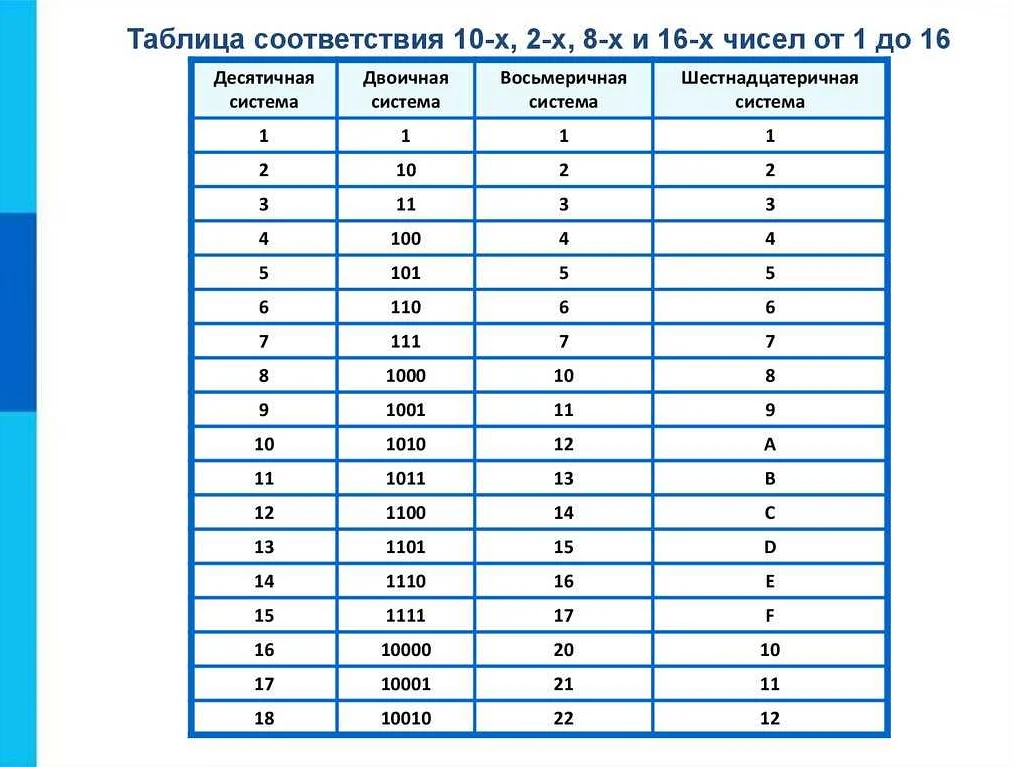
Римская система счисления была разработана в Древнем Риме и использовалась для записи чисел до введения арабской системы счисления. Она основана на использовании особых символов, которые представляют определенные значения.

Основные символы римской системы счисления:

• I — 1
• V — 5
• X — 10
• L — 50
• C — 100
• D — 500
• M — 1000

В римской системе счисления числа записываются путем суммирования или вычитания символов. При этом существуют определенные правила:

1. Символы записываются слева направо, начиная с наибольшего.
2. Если символ с меньшим значением стоит перед символом с большим значением, их значения складываются.
3. Если символ с меньшим значением стоит после символа с большим значением, значение первого символа вычитается из значения второго.
4. Не больше трех одинаковых символов подряд.
5. Единственное исключение — символы I, X и C могут повторяться четыре раза подряд для записи значения, равного 4, 9, 40, 90, 400 или 900.

Примеры чисел в римской системе счисления:

• 1 — I
• 5 — V
• 10 — X
• 50 — L
• 100 — C
• 500 — D
• 1000 — M
• 4 — IV
• 9 — IX
• 40 — XL
• 90 — XC
• 400 — CD
• 900 — CM

Римская система счисления имеет свои особенности и ограничения, но до сих пор используется для записи определенных чисел и в определенных областях, таких как история, нумизматика и т.д.

Системы счисления в компьютерах

Помимо двоичной системы, в компьютерах также используются восьмеричная и шестнадцатеричная системы счисления. Восьмеричная система основана на восьми цифрах — от 0 до 7, а шестнадцатеричная система — на шестнадцати цифрах, включающих десятичные цифры от 0 до 9 и буквы A, B, C, D, E, F.

Использование различных систем счисления в компьютерах обусловлено их внутренней аппаратурой. Компьютеры оперируют сигналами, которые могут принимать два состояния — высокое и низкое напряжение. Поэтому двоичная система счисления наиболее естественным образом соответствует внутренней работе компьютера.

Для удобства работы с большими числами в компьютерах используется также система счисления с плавающей точкой. В этой системе число представляется в виде мантиссы и порядка. Мантисса — это дробное число от 0 до 1, а порядок определяет положение десятичной точки и масштаб числа.

Изучение систем счисления в компьютерах позволяет понять, как числа представляются и обрабатываются внутри компьютера, а также осознать особенности работы с большими числами и десятичными дробями.

Преобразование чисел между системами счисления

Преобразование чисел из десятичной системы счисления в другие системы счисления (например, двоичную, восьмеричную или шестнадцатеричную) осуществляется путем последовательного деления числа на основание новой системы счисления и записи остатков от деления. Этот процесс повторяется до тех пор, пока исходное число не станет равным нулю.

Преобразование чисел из других систем счисления в десятичную систему осуществляется путем умножения каждой цифры числа на соответствующую степень основания системы счисления и последующего сложения результатов. Например, чтобы преобразовать число из двоичной системы в десятичную, каждую цифру числа нужно умножить на соответствующую степень двойки и сложить полученные результаты.

Преобразование чисел между системами счисления может быть полезно при работе с компьютерами и цифровой техникой, где двоичная система широко используется для представления данных. Также преобразование может быть полезно при решении задач в программировании и в других областях науки и техники.

Важно понимать особенности каждой системы счисления и знать алгоритмы преобразования чисел между ними. На практике часто используются специальные таблицы или программы для выполнения преобразования чисел между системами счисления, что упрощает и ускоряет процесс.

Особенности и применение различных систем счисления

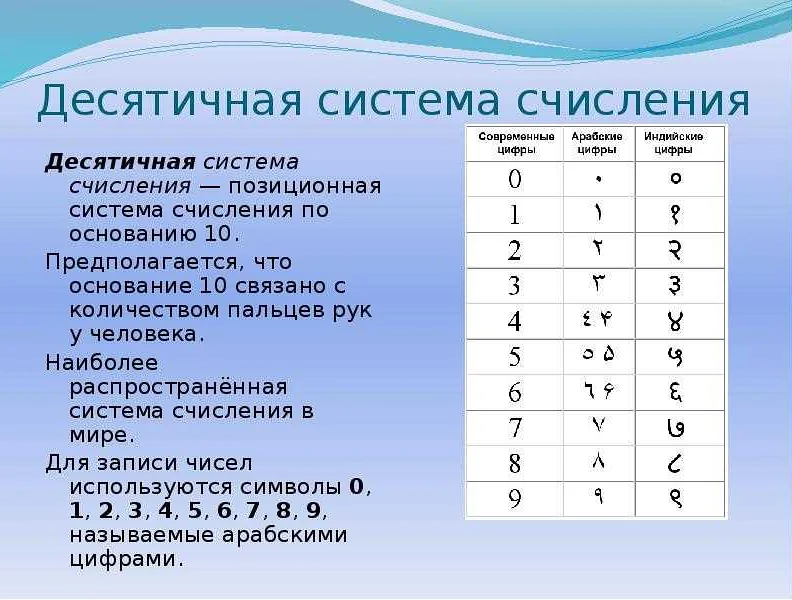
Десятичная система счисления является самой распространенной и широко используется в повседневной жизни. Она основана на использовании десяти цифр (от 0 до 9) и позиционной системе, в которой значение каждой цифры зависит от ее позиции в числе. Десятичная система широко применяется в международных стандартах, финансовых расчетах, измерениях и других областях.

Двоичная система счисления использует только две цифры — 0 и 1. Она является основной системой счисления в компьютерах и информатике, так как легко преобразуется в электрические сигналы. В двоичной системе каждая цифра называется битом (binary digit), а числа представляются последовательностью битов. Двоичная система также широко используется в кодировании и шифровании данных.

Восьмеричная система счисления использует восемь цифр (от 0 до 7). Восьмеричная система удобна для представления двоичных чисел, так как каждая группа трех битов может быть представлена одной восьмеричной цифрой. Восьмеричная система использовалась в прошлом в компьютерах и программировании, но с развитием технологий она потеряла свою популярность.

Шестнадцатеричная система счисления использует шестнадцать цифр (от 0 до 9 и от A до F). Шестнадцатеричная система широко применяется в программировании и компьютерной технике, так как компактно представляет большие числа и удобна для работы с двоичными числами. В шестнадцатеричной системе буквы A, B, C, D, E и F обозначают значения от 10 до 15 соответственно.

Кроме перечисленных систем счисления, существуют и другие, такие как троичная (система счисления на основе трех цифр), пятичная (система счисления на основе пяти цифр) и др. Они могут использоваться в специфических областях, где требуются особые математические операции и представления чисел.

Понимание различных систем счисления важно для программистов, математиков и инженеров, которые работают с числами и выполняют различные математические операции. Каждая система счисления имеет свои преимущества и недостатки, и выбор подходящей системы зависит от конкретной задачи и контекста использования.

Вопрос-ответ:

Какие виды систем счисления существуют в математике?

В математике существует несколько видов систем счисления, включая десятичную, двоичную, восьмеричную и шестнадцатеричную системы счисления.

В чем особенности десятичной системы счисления?

Десятичная система счисления основана на числе 10 и использует 10 различных цифр: от 0 до 9. В этой системе каждая цифра имеет свое значение в зависимости от ее позиции в числе. Например, число 123 представляет собой 1 * 10^2 + 2 * 10^1 + 3 * 10^0.

Что такое двоичная система счисления и для чего она используется?

Двоичная система счисления основана на числе 2 и использует только две цифры: 0 и 1. В этой системе каждая цифра имеет свое значение в зависимости от ее позиции в числе. Двоичная система широко используется в компьютерах и электронике, так как компьютеры работают с двоичными данными.

Как работает восьмеричная система счисления?

Восьмеричная система счисления основана на числе 8 и использует восемь различных цифр: от 0 до 7. В этой системе каждая цифра имеет свое значение в зависимости от ее позиции в числе. Например, число 123 представляет собой 1 * 8^2 + 2 * 8^1 + 3 * 8^0. Восьмеричная система счисления редко используется в повседневной жизни, но может быть полезной при работе с определенными типами данных или в программировании.

Что такое шестнадцатеричная система счисления и как она работает?

Шестнадцатеричная система счисления основана на числе 16 и использует шестнадцать различных цифр: от 0 до 9 и от A до F. В этой системе каждая цифра имеет свое значение в зависимости от ее позиции в числе. Шестнадцатеричная система широко используется в компьютерах и программировании, так как она позволяет компактно представлять большие числа и битовые данные.