Что из перечисленного является математической моделью

Математическая модель представляет собой абстрактное описание реальной системы или явления с использованием математических понятий и формул. Узнайте, что из списка можно рассматривать как математическую модель и как она помогает в понимании и анализе различных процессов.

Математическая модель — это абстрактное представление реального объекта, явления или системы с помощью математических символов и отношений. Она используется для описания и изучения различных процессов и явлений в различных областях науки, от физики и биологии до экономики и социологии.

Основная цель создания математической модели — это упрощение сложных и многообразных процессов, чтобы можно было исследовать их характеристики и свойства, а также делать прогнозы и принимать решения на основе этих моделей. Математические модели могут быть как аналитическими (в виде уравнений и формул), так и графическими (в виде диаграмм и графиков).

Определение математической модели может происходить по различным критериям. Во-первых, модель должна быть точной и достаточно адекватной реальной системе, чтобы описывать ее основные закономерности и характеристики. Во-вторых, модель должна быть простой и понятной для анализа, чтобы исследователи и специалисты могли использовать ее в своей работе и принимать на ее основе обоснованные решения. В-третьих, модель должна быть верифицированной и проверенной на основе экспериментальных данных и наблюдений, чтобы ее результаты были достоверными и достоверными.

Таким образом, математическая модель — это инструмент, который позволяет упрощать и анализировать сложные системы и процессы, а также делать прогнозы и принимать решения на основе этих анализов. Она играет важную роль в различных областях науки и техники и помогает нам лучше понимать окружающий мир и наши взаимодействия с ним.

Что такое математическая модель?

Математическая модель может быть использована для анализа, прогнозирования, оптимизации и управления различными системами и процессами. Она позволяет исследовать взаимодействие различных факторов и предсказывать результаты изменений в условиях эксперимента или реальной практики.

Математические модели часто используются в науке, инженерии, экономике, биологии, физике и других областях знания. Они позволяют решать сложные задачи, которые не всегда могут быть решены другими методами. Математические модели могут быть простыми или сложными, статическими или динамическими, аналитическими или численными.

Определение и построение математической модели требуют точного и ясного определения целей и задач исследования или практической работы. Они также требуют разработки и использования соответствующих математических методов, уравнений и алгоритмов.

Почему математическая модель важна?

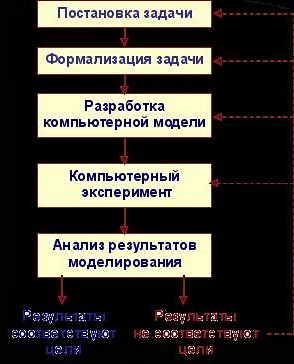
Одним из основных преимуществ математических моделей является их предсказательная способность. Используя модель, мы можем провести различные эксперименты и предсказать результаты без необходимости проводить дорогостоящие и времязатратные физические эксперименты.

Математическая модель также позволяет упростить сложные проблемы до более простых и понятных. Она помогает разбить сложное явление на составляющие и понять, как взаимодействуют эти составляющие между собой.

Еще одним важным преимуществом математической модели является возможность представления и визуализации данных. Модель позволяет создать графики, диаграммы и другие визуальные представления, что значительно облегчает понимание и анализ полученных результатов.

Наконец, математическая модель позволяет проводить различные сценарные анализы и оптимизацию. Мы можем изменять параметры модели и смотреть, как это влияет на ее поведение и результаты. Таким образом, модель помогает принимать более обоснованные решения и выбирать оптимальные стратегии в различных ситуациях.

Определение математической модели

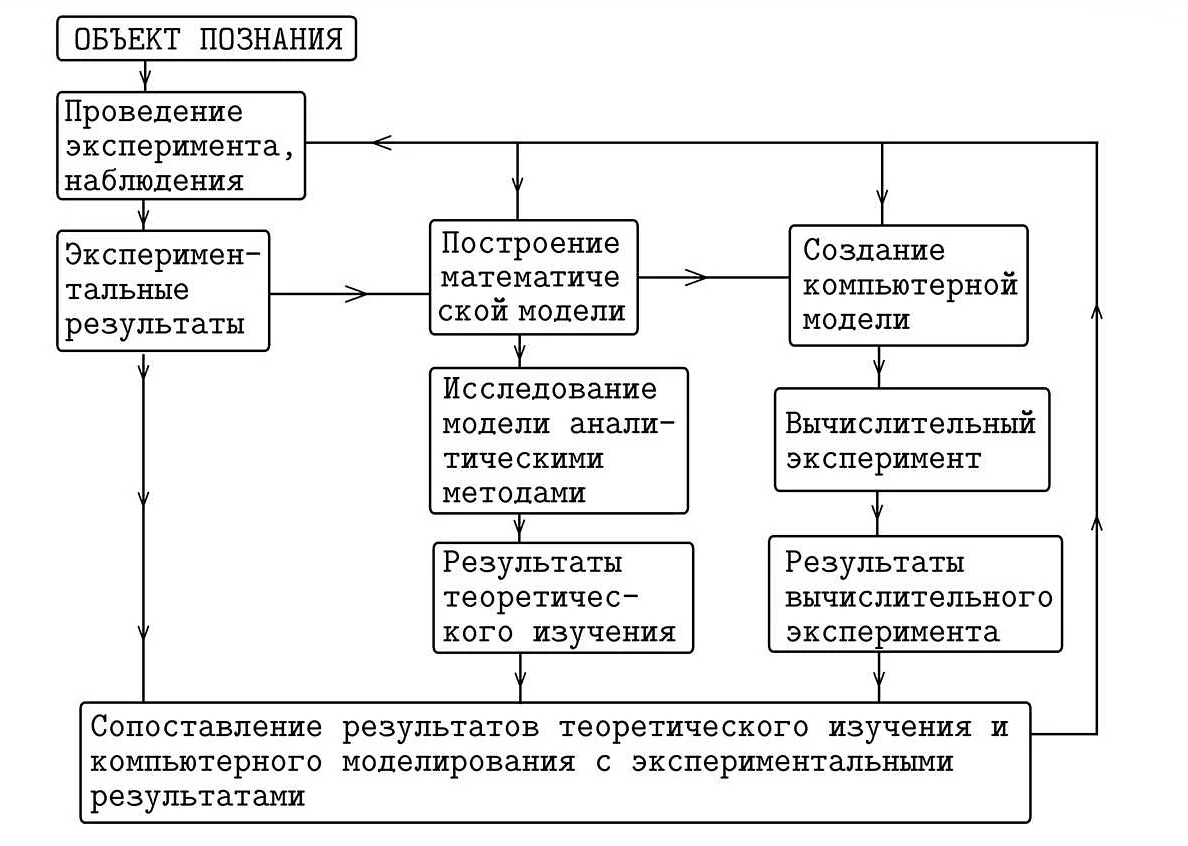
Определение математической модели требует определения следующих элементов:

1. Объект моделирования: реальное явление или процесс, которое мы хотим изучить с помощью математической модели. Это может быть физический объект, биологическая система, экономический процесс и т.д.
2. Переменные: параметры, которые характеризуют состояние или свойства объекта моделирования. Они могут быть количественными (например, время, расстояние) или качественными (например, категории, состояния).
3. Уравнения и соотношения: математические выражения, которые связывают переменные и описывают взаимодействия между ними. Они могут быть дифференциальными, алгебраическими или стохастическими.
4. Параметры: значения, которые определяют свойства или условия модели. Они могут быть известными или неизвестными и могут быть получены из экспериментальных данных или других источников.
5. Решение модели: процесс нахождения значений переменных, которые удовлетворяют уравнениям модели и заданным параметрам. Решение модели может быть аналитическим или численным.

Математические модели широко применяются в разных областях науки, техники и экономики для предсказания и оптимизации различных процессов и систем. Они позволяют более глубоко понять и изучить сложные явления, а также принимать обоснованные решения на основе математического анализа и моделирования.

Как определить математическую модель?

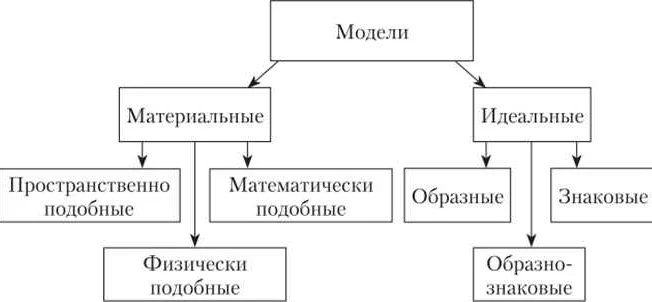
Для определения математической модели необходимо:

1. Изучить объект или систему, которую требуется описать математически.
2. Выделить ключевые переменные, факторы и параметры, которые влияют на объект или систему.
3. Установить связи и зависимости между переменными, факторами и параметрами.
4. Сформулировать математические уравнения или систему уравнений, которые отражают эти связи и зависимости.
5. Проверить и адаптировать модель с помощью экспериментов, наблюдений или сбора данных.

При определении математической модели важно учитывать особенности и специфику объекта или системы, а также уровень детализации и точности моделирования, которые требуются в конкретной задаче или исследовании.

Математическая модель может быть использована для прогнозирования, оптимизации, анализа и управления объектами и системами в различных областях, таких как физика, экономика, биология, социология и технические науки.

Какие методы использовать для определения математической модели?

Определение математической модели требует применения различных методов и подходов. Вот некоторые из них:

• Эмпирический метод: данный метод основан на экспериментальных данных и наблюдениях. Используя результаты экспериментов, можно вывести законы и связи, которые затем могут быть представлены в виде математической модели.
• Аналитический метод: данный метод используется для анализа и построения моделей на основе известных математических законов и формул. Он позволяет определить связи между переменными и описать их в виде уравнений или систем уравнений.
• Статистический метод: данный метод используется для анализа большого объема данных и определения статистических закономерностей. Он позволяет построить математическую модель, основанную на вероятностных распределениях и статистических параметрах.
• Символьный метод: данный метод основан на использовании символьных вычислений и алгебры. Он позволяет работать с символами и выражениями, что упрощает анализ и решение математических задач.
• Численный метод: данный метод основан на численных вычислениях и приближенных методах. Он позволяет решать сложные математические задачи, используя компьютерные алгоритмы и программы.

Каждый из этих методов имеет свои преимущества и ограничения, и выбор метода зависит от конкретной задачи и доступных данных. Часто комбинирование различных методов позволяет получить более точные и полные математические модели.

Примеры математических моделей

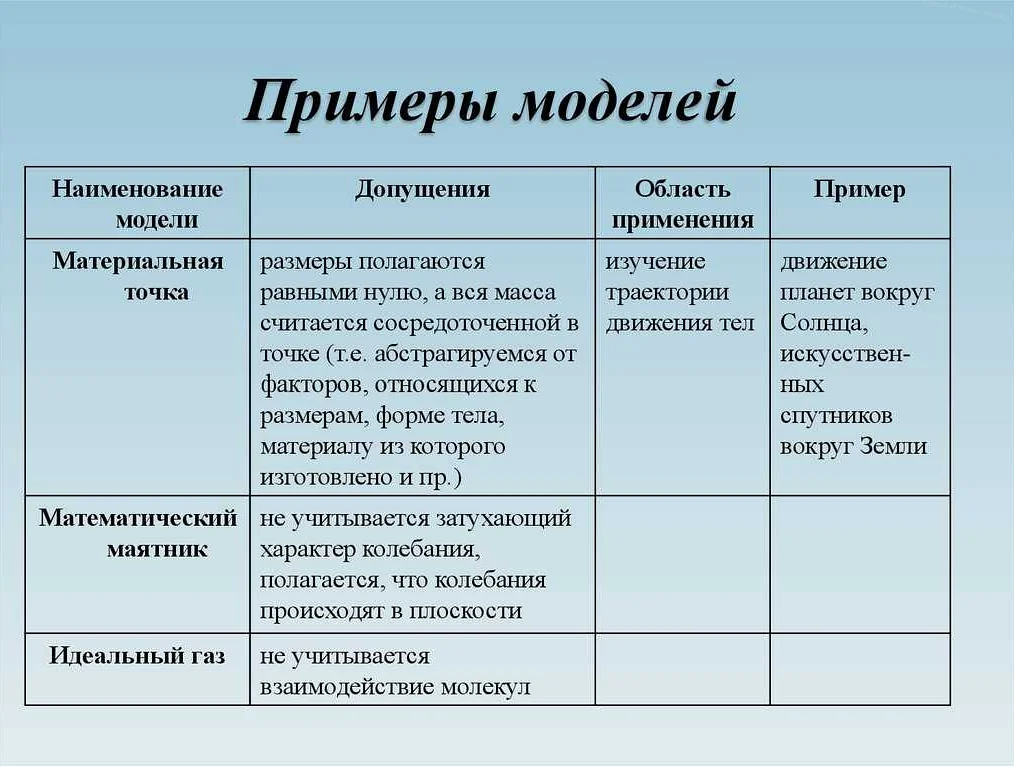
Математические модели широко применяются в различных областях науки, техники и экономики. Вот несколько примеров:

1. Модель экономического роста: используется для анализа и прогнозирования экономического развития страны или региона. Включает в себя различные факторы, такие как инвестиции, потребление, инфляция и т.д.

2. Модель распространения эпидемии: используется для изучения и прогнозирования распространения инфекционных заболеваний. Учитывает факторы, такие как скорость передачи, степень защиты населения, иммунитет и т.д.

3. Модель движения планет: используется для изучения и предсказания движения планет в солнечной системе. Учитывает гравитационные силы, массы и расстояния между планетами.

4. Модель теплопроводности: используется для изучения распределения тепла в твердых телах. Учитывает теплопроводность материала, температуру и граничные условия.

5. Модель очереди: используется для изучения и оптимизации систем обслуживания с очередями, например, для определения оптимального количества обслуживающих устройств или минимизации среднего времени ожидания.

Это лишь некоторые примеры математических моделей, которые помогают нам лучше понять и предсказать реальные явления и процессы.

Вопрос-ответ:

Зачем нужна математическая модель?

Математическая модель позволяет описать сложные явления и процессы в упрощенной форме, используя математические методы и уравнения. Она помогает предсказывать и анализировать поведение системы, проводить эксперименты на компьютере, исследовать различные сценарии и принимать обоснованные решения.

Как определить математическую модель?

Определение математической модели зависит от конкретного объекта или процесса, который мы хотим изучить. Для этого требуется собрать и проанализировать данные, провести эксперименты или наблюдения. Затем необходимо выделить основные параметры и взаимосвязи между ними, на основе которых можно построить математическую модель.

Какие методы использовать для построения математической модели?

Для построения математической модели можно использовать различные методы, в зависимости от конкретной задачи и доступных данных. Возможные подходы включают статистические методы, дифференциальные уравнения, оптимизацию, вероятностные модели и другие. Важно выбрать подходящий метод и проверить его адекватность с помощью экспериментов и сравнения с реальными данными.

Как проверить адекватность математической модели?

Для проверки адекватности математической модели необходимо провести сравнение результатов моделирования с реальными данными или экспериментами. Если модель дает достаточно точные прогнозы, согласующиеся с наблюдениями, то можно считать ее адекватной. Если же результаты моделирования сильно расходятся с реальными данными, то требуется корректировка модели или выбор другого подхода.

Какие ограничения у математической модели?

Математическая модель не может учесть все детали и особенности реальной системы или процесса. Она всегда является упрощенным представлением и может игнорировать некоторые факторы, которые могут оказывать влияние на результаты. Кроме того, модель может быть чувствительна к начальным условиям или параметрам, которые могут быть сложно определить точно. Поэтому необходимо быть осторожным при применении и интерпретации результатов математической модели.

Каково определение математической модели?

Математическая модель — это абстрактное представление реальной системы или процесса с использованием математических символов и формул. Она позволяет описать и анализировать различные аспекты системы, такие как ее поведение, свойства и взаимодействия.

Зачем нужна математическая модель?

Математическая модель позволяет упростить сложные системы и процессы, представив их в виде математических уравнений и формул. Она помогает предсказывать поведение системы в различных условиях, оптимизировать ресурсы, а также анализировать и проверять гипотезы и предположения без риска для реальных объектов или процессов.

Примеры применения математических моделей в реальной жизни

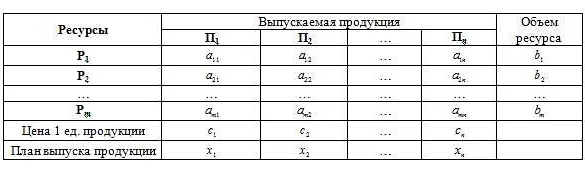
Вот некоторые примеры применения математических моделей в различных сферах жизни:

1. Финансы: Математические модели используются для анализа финансовых рынков, прогнозирования цен на акции и определения оптимальных стратегий инвестирования.
2. Транспорт: Математические модели помогают оптимизировать расписание транспортных средств, улучшить эффективность движения и уменьшить заторы на дорогах.
3. Медицина: Математические модели используются для анализа распространения заболеваний, разработки лекарственных препаратов и оптимизации лечебных процедур.
4. Экология: Математические модели позволяют анализировать экологические системы, прогнозировать изменения в окружающей среде и разрабатывать стратегии охраны природы.
5. Инженерия: Математические модели используются для проектирования и оптимизации различных систем, таких как авиационные двигатели, электронные устройства и структуры зданий.

Это лишь некоторые примеры применения математических моделей, их применение может быть найдено во многих других областях, включая экономику, социологию, политику и даже искусство.

Видео по теме: