Что общего и в чем различие понятий математическая модель и компьютерная математическая модель
Содержимое
- 1 Что общего и в чем различие понятий математическая модель и компьютерная математическая модель
- 1.1 Определение математической модели
- 1.2 Видео по теме:
- 1.3 Цель математической моделирования
- 1.4 Применение математической модели
- 1.5 Определение компьютерной математической модели
- 1.6 Роль компьютерной математической модели
- 1.7 Преимущества компьютерной математической модели
- 1.8 Сходства математической модели и компьютерной математической модели
- 1.9 Различия математической модели и компьютерной математической модели
- 1.10 Вопрос-ответ:
- 1.10.0.1 Какие сходства есть между математической моделью и компьютерной математической моделью?
- 1.10.0.2 В чем различия между математической моделью и компьютерной математической моделью?
- 1.10.0.3 Какие примеры математических моделей и компьютерных математических моделей можно привести?
- 1.10.0.4 Зачем нужны математические модели и компьютерные математические модели?
- 1.10.0.5 Каковы ограничения математических моделей и компьютерных математических моделей?
- 1.10.0.6 Какие сходства есть между математической моделью и компьютерной математической моделью?
- 1.10.0.7 Какие различия есть между математической моделью и компьютерной математической моделью?
Статья рассказывает о понятиях математическая модель и компьютерная математическая модель, их связи и различиях. Узнайте, как эти понятия используются в науке и технологиях, и как они помогают в решении сложных математических задач.
Математическая модель — это абстрактное представление реального объекта или явления, основанное на математических принципах и формулах. Она позволяет описать и изучить свойства и поведение системы, а также проводить различные эксперименты и предсказывать будущие события. Математические модели широко используются во многих областях науки, техники и экономики.
Тем не менее, математическая модель имеет свои ограничения. Во-первых, она является упрощенным представлением реальной системы, и поэтому может не полностью отражать ее сложность и все взаимосвязи. Во-вторых, математическая модель не может учесть все факторы, влияющие на систему, и поэтому ее результаты могут быть приближенными и не всегда точными.
В отличие от математической модели, компьютерная математическая модель использует вычислительные технологии для создания более точного и полного представления системы. Она позволяет учесть большее количество факторов, проводить более сложные и точные расчеты, а также визуализировать результаты моделирования.
Компьютерная математическая модель может быть использована для решения различных задач, таких как оптимизация процессов, прогнозирование будущих событий, анализ и синтез систем.
Однако, несмотря на все преимущества, компьютерная математическая модель также имеет свои ограничения. Во-первых, создание и поддержка такой модели требует больших вычислительных ресурсов и времени. Во-вторых, компьютерная модель может быть неполной или некорректной из-за неточности входных данных или ошибок в алгоритмах. Кроме того, результаты моделирования могут зависеть от выбранного программного обеспечения и параметров модели, что может привести к различным и непредсказуемым результатам.
Определение математической модели
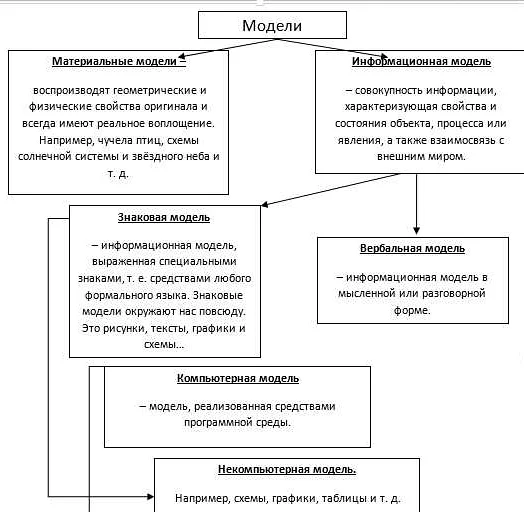
Математическая модель может быть представлена в виде уравнений, систем уравнений, графов, диаграмм и других математических объектов. Она позволяет выявить взаимосвязи между различными факторами и позволяет анализировать их влияние на систему в целом.
Основная цель математической модели — предоставить возможность прогнозирования поведения системы на основе известных начальных данных. Она может быть использована для изучения различных вариантов развития событий, определения оптимальных решений или предсказания результатов экспериментов.
Математическая модель является универсальным инструментом, который применяется во многих областях науки и техники. Она позволяет проводить исследования и эксперименты в виртуальной среде, что позволяет существенно сократить затраты на проведение реальных экспериментов и оптимизировать процессы проектирования и управления системами.
Преимущества математических моделейНедостатки математических моделей
| Позволяют проводить анализ и прогнозирование поведения системы | Не всегда могут учесть все факторы, влияющие на систему |
| Позволяют проводить виртуальные эксперименты | Требуют наличия точных данных для построения модели |
| Сокращают затраты на проведение реальных экспериментов | Могут быть сложными и требовать высокого уровня математической подготовки |
| Позволяют оптимизировать процессы проектирования и управления системами | Могут давать только приближенные результаты |
Видео по теме:
Цель математической моделирования

Процесс математического моделирования позволяет установить зависимости между различными переменными и параметрами системы, а также предсказывать ее поведение в различных условиях. Математические модели могут быть использованы для прогнозирования будущих событий, оптимизации систем, анализа рисков и принятия решений.
Целью математического моделирования является также проверка гипотез и теорий, а также экспериментальная проверка результатов. Математические модели могут служить инструментом для проведения виртуальных экспериментов, что позволяет сэкономить время и ресурсы, которые могут понадобиться для реальных экспериментов.
Кроме того, математическое моделирование способствует лучшему пониманию сложных систем и процессов, и позволяет разработать и оптимизировать различные методы и алгоритмы для их анализа и управления.
Таким образом, цель математической моделирования заключается в создании упрощенной, но все еще репрезентативной модели реальных явлений и систем, которая позволяет исследовать их свойства, предсказывать и оптимизировать их поведение, а также проверять гипотезы и теории.
Применение математической модели

Одним из основных применений математической модели является прогнозирование. Математические модели позволяют предсказывать будущее поведение системы или процесса на основе имеющихся данных и параметров. Например, математические модели используются для прогнозирования погоды, экономических показателей, распространения эпидемий и т.д.
Еще одним применением математической модели является оптимизация. Математические модели позволяют находить оптимальные решения для различных задач. Например, они используются в экономике для определения оптимальных планов производства и распределения ресурсов, в логистике для оптимизации маршрутов доставки и т.д.
Математические модели также применяются в научных исследованиях. Они позволяют проводить эксперименты в виртуальной среде, что может быть невозможно в реальности. Например, математические модели используются в физике, химии, биологии для изучения различных физических, химических и биологических процессов.
Кроме того, математические модели применяются в инженерии и технике. Они позволяют проектировать и оптимизировать различные системы и устройства, такие как самолеты, машины, компьютеры и т.д. Например, математические модели используются в автопроме для оптимизации конструкции автомобилей и улучшения их характеристик.
В целом, применение математической модели в различных областях науки и техники позволяет получить новые знания, решить сложные задачи и улучшить существующие процессы и системы.
Определение компьютерной математической модели

Компьютерные математические модели широко применяются в различных областях, таких как физика, химия, биология, экономика, инженерия и др. Они позволяют исследовать сложные системы, которые трудно или невозможно изучать аналитически, а также проводить эксперименты и тестирования в виртуальной среде.
Одним из основных преимуществ компьютерных математических моделей является возможность быстрого и эффективного анализа больших объемов данных, проведения численных расчетов и моделирования различных сценариев. Они также позволяют визуализировать результаты моделирования и представить их в понятной форме для принятия решений.
Компьютерная математическая модель обычно состоит из математического описания системы в виде уравнений, алгоритмов и параметров, которые влияют на поведение модели. Она может быть статической или динамической, дискретной или непрерывной, линейной или нелинейной в зависимости от характера исследуемой системы.
Однако следует отметить, что компьютерная математическая модель не является полной идеализацией реальности и всегда содержит некоторую степень приближения и упрощения. Она может быть верифицирована и валидирована с помощью сравнения ее результатов с экспериментальными данными или другими моделями.
Таким образом, компьютерная математическая модель является мощным инструментом для исследования и анализа сложных систем, которые требуют математического описания и численного моделирования.
Роль компьютерной математической модели
Одной из важных ролей компьютерной математической модели является возможность проведения экспериментов и исследований в виртуальной среде. Это позволяет сэкономить время и ресурсы, которые могут потребоваться при проведении аналогичных исследований в реальности. Кроме того, компьютерная модель позволяет проводить эксперименты с различными параметрами и условиями, которые могут быть трудно или невозможно реализовать в реальной среде.
Компьютерная математическая модель также позволяет проводить численные расчеты и прогнозы, которые могут быть полезны для принятия решений. Например, она может использоваться для моделирования погоды, расчета физических процессов, оптимизации производственных процессов и т.д. Результаты таких расчетов могут быть использованы для прогнозирования будущих событий или определения оптимальных стратегий.
Важной особенностью компьютерной математической модели является ее гибкость и масштабируемость. Она может быть изменена и доработана в зависимости от поставленных задач и требований. Кроме того, компьютерная модель может быть масштабирована для работы с большими объемами данных или сложными системами.
Таким образом, компьютерная математическая модель играет важную роль в научных исследованиях, инженерных расчетах, прогнозировании и оптимизации процессов. Она позволяет более глубоко изучать явления и процессы, создавать новые знания и принимать обоснованные решения.
Преимущества компьютерной математической модели
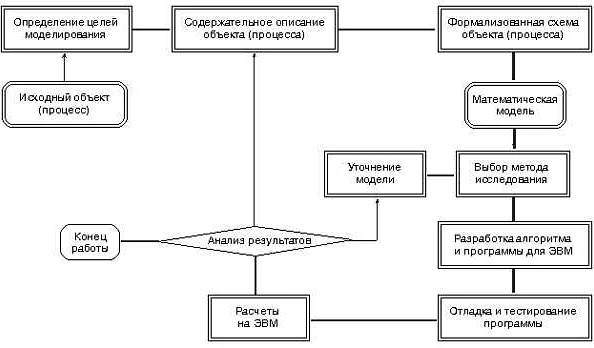
- Большая точность: Компьютерная математическая модель позволяет использовать более точные и сложные математические методы и алгоритмы для анализа данных. Это позволяет получить более точные результаты и предсказания.
- Большая скорость расчетов: Компьютерные математические модели позволяют проводить расчеты и моделирование значительно быстрее, чем вручную. Это позволяет экономить время и ресурсы и ускоряет процесс принятия решений.
- Возможность моделирования сложных систем: Компьютерная математическая модель позволяет моделировать системы с большим количеством переменных и сложными взаимодействиями между ними. Это позволяет исследовать и предсказывать поведение сложных систем, которое может быть трудно представить в аналоговой модели.
- Возможность проведения экспериментов и тестирования: Компьютерные математические модели позволяют проводить виртуальные эксперименты и тестирование различных сценариев. Это позволяет оценить эффективность различных стратегий и прогнозировать результаты.
- Возможность визуализации и анализа результатов: Компьютерная математическая модель позволяет визуализировать и анализировать результаты моделирования с помощью графиков, диаграмм и других визуальных средств. Это упрощает восприятие и анализ информации и позволяет выявить скрытые закономерности и тренды.
В целом, компьютерная математическая модель является мощным инструментом для анализа, исследования и прогнозирования различных явлений и процессов. Она позволяет получить более точные и быстрые результаты, а также проводить виртуальные эксперименты и анализировать полученные данные.
Сходства математической модели и компьютерной математической модели

Одно из основных сходств между математической моделью и компьютерной математической моделью заключается в том, что обе они основываются на математических принципах и используются для решения задач с помощью математических методов. Они оба представляют собой системы уравнений и формул, которые описывают взаимодействие различных переменных и параметров.
Кроме того, и математическая модель, и компьютерная математическая модель оба требуют определения начальных условий и параметров для правильного функционирования. Например, при моделировании движения тела в пространстве, необходимо знать начальные координаты и скорости, а также значения различных физических параметров, таких как масса и сила трения.
Оба типа моделей также могут быть использованы для прогнозирования будущих событий и явлений. С помощью математических методов и компьютерных алгоритмов можно предсказать траекторию движения объекта, проанализировать поведение финансовых рынков или предсказать распространение эпидемии.
Наконец, и математическая модель, и компьютерная математическая модель могут быть использованы для оптимизации систем и процессов. Они могут помочь найти оптимальные значения переменных или параметров для достижения определенных целей или результатов.
Таким образом, сходства между математической моделью и компьютерной математической моделью заключаются в использовании математических методов, определении начальных условий и параметров, возможности прогнозирования и оптимизации различных явлений и процессов.
Различия математической модели и компьютерной математической модели
Математическая модель представляет собой формализованное описание объекта или процесса с помощью математических символов, формул и уравнений. Она позволяет описать и изучить свойства и поведение системы в рамках определенных предположений и условий. Математическая модель обычно представляется в виде аналитических выражений, которые могут быть решены аналитически или численно.
Компьютерная математическая модель, в свою очередь, является численным представлением математической модели с помощью компьютерной программы. Она представляет собой набор алгоритмов и вычислений, которые позволяют смоделировать поведение системы и получить численные результаты. Компьютерная математическая модель может быть более точной и реалистичной, так как позволяет учитывать сложные и нелинейные взаимодействия.
Кроме того, компьютерная математическая модель позволяет проводить численные эксперименты, изменяя параметры модели и анализируя результаты. Это позволяет исследовать различные сценарии и прогнозировать поведение системы в различных условиях. Математическая модель, в свою очередь, ограничена возможностями аналитического решения и не всегда позволяет проводить такие эксперименты.
Математическая модельКомпьютерная математическая модель
| Абстракция реального объекта или процесса | Численная реализация абстракции |
| Аналитические выражения | Численные алгоритмы и вычисления |
| Ограниченные возможности аналитического решения | Возможность проведения численных экспериментов |
Вопрос-ответ:
Какие сходства есть между математической моделью и компьютерной математической моделью?
Математическая модель и компьютерная математическая модель оба представляют собой абстракции реальных объектов или систем. Они оба используют математические уравнения и методы, чтобы описать их поведение.
В чем различия между математической моделью и компьютерной математической моделью?
Основное различие между ними заключается в способе представления модели. Математическая модель обычно представлена аналитическими уравнениями, которые могут решаться аналитически или численно. Компьютерная математическая модель, с другой стороны, представлена в виде программного кода, который может быть запущен на компьютере для выполнения вычислений и анализа модели.
Какие примеры математических моделей и компьютерных математических моделей можно привести?
Примеры математических моделей включают модель распространения эпидемии, модель популяционной динамики и модель теплопроводности. Примеры компьютерных математических моделей включают компьютерную симуляцию погоды, компьютерную симуляцию автомобильного движения и компьютерную симуляцию физических процессов.
Зачем нужны математические модели и компьютерные математические модели?
Математические модели и компьютерные математические модели используются для прогнозирования поведения системы, исследования различных сценариев и оптимизации процессов. Они могут помочь в принятии рациональных решений, позволяют проводить экономически эффективные исследования и эксперименты, а также позволяют сократить затраты на эксперименты в лабораторных условиях.
Каковы ограничения математических моделей и компьютерных математических моделей?
Ограничения математических моделей и компьютерных математических моделей включают предположения, сделанные при разработке модели, аппроксимации, которые могут быть не совсем точными, и ограниченные возможности моделирования сложных систем. Они также могут быть чувствительны к начальным условиям и параметрам модели, что может привести к неточным результатам.
Какие сходства есть между математической моделью и компьютерной математической моделью?
Между математической моделью и компьютерной математической моделью есть несколько сходств. Во-первых, обе модели используются для описания и анализа различных явлений и процессов в реальном мире. Во-вторых, в обеих моделях используются математические формулы и уравнения для представления этих явлений. В-третьих, как математическая модель, так и компьютерная математическая модель могут быть использованы для прогнозирования и тестирования различных сценариев на основе имеющихся данных.
Какие различия есть между математической моделью и компьютерной математической моделью?
Различия между математической моделью и компьютерной математической моделью заключаются в способах их представления и использования. Математическая модель представляет собой аналитическое описание явления или процесса с использованием математических уравнений и формул. Компьютерная математическая модель, в отличие от этого, представляет собой численную реализацию математической модели с использованием компьютерных программ. Кроме того, компьютерная математическая модель может быть более сложной и точной, так как компьютер может выполнять большое количество вычислений и обрабатывать большие объемы данных.
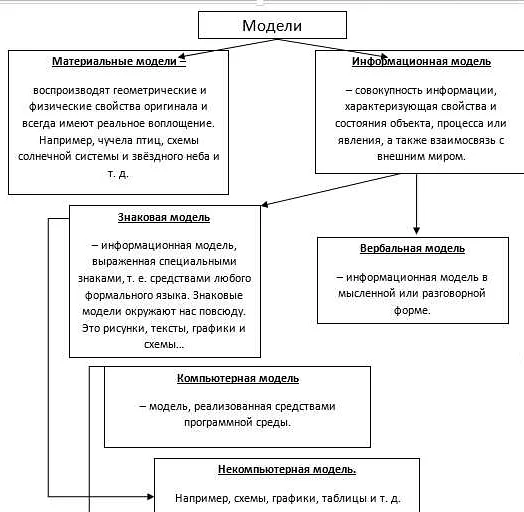

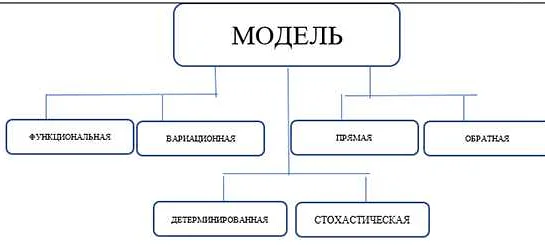

Математическая модель и компьютерная математическая модель — это два понятия, которые иногда вызывают путаницу. Однако, они имеют как сходства, так и различия. Оба типа моделей используются для описания и анализа сложных процессов, явлений и систем. Они представляют собой абстрактные конструкции, которые позволяют нам изучать и понимать реальный мир. Как математическая, так и компьютерная модель основаны на математических принципах и используют математические формулы, уравнения и алгоритмы. Однако, различия между ними тоже существуют. Математическая модель является более абстрактной и теоретической, она представляет собой набор математических формул и уравнений, которые описывают свойства и взаимодействия системы. Она не зависит от конкретных вычислительных ресурсов и может быть использована для анализа систем различного размера и сложности. В то же время, компьютерная математическая модель представляет собой реализацию математической модели в виде программного кода, который может быть выполнен на компьютере. Она позволяет проводить численное моделирование и симуляцию процессов в реальном времени. Компьютерная модель может быть более точной и реалистичной, так как она учитывает больше факторов и параметров системы. В итоге, как математическая, так и компьютерная математическая модель играют важную роль в науке, инженерии и других областях. Они предоставляют нам инструменты для предсказания и оптимизации процессов, разработки новых технологий и принятия важных решений. Понимание сходств и различий между ними поможет нам использовать их эффективно и достичь лучших результатов.
Статья очень интересная и понятная. Она помогла мне лучше понять, что такое математическая модель и компьютерная математическая модель. Я узнал, что математическая модель является абстракцией реального объекта или явления, а компьютерная математическая модель – это конкретная реализация математической модели, выполненная на компьютере. Кроме того, статья рассказала о том, что математическая модель может быть представлена в виде уравнений, а компьютерная математическая модель может быть реализована с помощью программного обеспечения. Мне особенно понравилось, как автор объяснил различия между этими двумя типами моделей. Он указал на то, что компьютерная математическая модель позволяет учитывать больше параметров и сложных взаимодействий, чем математическая модель. Кроме того, компьютерная модель позволяет проводить более точные и быстрые вычисления, что делает ее очень полезной для решения сложных проблем. В целом, статья была очень информативной и полезной для меня. Она помогла мне лучше понять суть математических моделей и их применение в реальной жизни. Теперь я осознаю, что компьютерные математические модели являются мощным инструментом для анализа и прогнозирования различных явлений. Спасибо автору за такую интересную статью!