Что называют математической моделью управления

Математическая модель управления — это формализованное представление системы управления в виде математических уравнений и алгоритмов. Она позволяет описывать и анализировать процессы управления с помощью методов математического моделирования и оптимизации.

Математическая модель управления – это абстрактная математическая конструкция, которая позволяет описать и анализировать процессы управления в различных сферах деятельности. Она представляет собой набор математических уравнений и формул, которые описывают зависимости между входными и выходными параметрами системы управления.

Основная задача математической модели управления заключается в том, чтобы найти оптимальное управление системой при заданных ограничениях и условиях. Для этого необходимо сформулировать цель управления, определить входные и выходные параметры системы, а также учесть все ограничения и факторы, которые могут повлиять на процесс управления.

Принципы математической модели управления включают в себя системный подход, принцип оптимальности, адекватность и простоту модели. Системный подход предполагает рассмотрение системы управления как совокупности взаимосвязанных элементов, каждый из которых влияет на работу системы в целом. Принцип оптимальности заключается в том, что модель должна найти такое управление, которое обеспечивает наилучший результат с учетом заданных ограничений и условий.

Адекватность модели означает, что она должна точно отражать основные характеристики и зависимости в реальной системе управления. Простота модели – это требование к минимальному количеству используемых параметров и уравнений, чтобы упростить и ускорить анализ и решение задач управления.

Что такое математическая модель управления?

Математическая модель управления включает в себя следующие компоненты:

КомпонентОписание

Объект управления	Система или процесс, который подвергается управлению. Может быть физическим объектом, экономической системой, социальным объектом и т.д.
Управляющее воздействие	Воздействие, которое применяется к объекту управления для достижения заданных целей. Может быть представлено в виде сигналов, команд, параметров и т.д.
Измерение	Процесс получения информации о состоянии объекта управления. Может быть осуществлен с помощью датчиков, измерительных приборов и т.д.
Модель системы	Математическое описание объекта управления, которое связывает управляющее воздействие с измерением. Модель может быть линейной или нелинейной, статической или динамической.
Алгоритм управления	Правила и методы, которые определяют, каким образом управляющее воздействие должно быть применено к объекту управления на основе измерения и модели системы. Алгоритм может быть простым или сложным, оптимальным или эвристическим.
Цель управления	Желаемое состояние или поведение объекта управления, которое должно быть достигнуто с помощью управления. Целью может быть минимизация ошибки, устранение отклонений от заданного значения, оптимизация производительности и т.д.

Математическая модель управления позволяет анализировать и оптимизировать системы управления на основе точных математических методов. Она является основой для разработки алгоритмов управления и позволяет предсказывать результаты управляющих воздействий на объект управления.

Видео по теме:

Важность математической модели в управлении

Математическая модель может быть применена в различных областях управления, таких как производство, финансы, логистика и другие. Она позволяет описать сложные системы и их взаимодействие, а также предсказать последствия различных решений.

Одной из основных причин использования математической модели является возможность упрощения анализа и принятия решений. За счет формализации и структурирования информации, модель позволяет учитывать множество факторов и вариантов развития ситуаций. Таким образом, она помогает управляющим принимать обоснованные и оптимальные решения на основе объективных данных.

Еще одним важным аспектом математической модели является возможность проведения экспериментов и оптимизации управленческих процессов. С ее помощью можно проводить различные сценарные моделирования и анализировать их результаты. Это позволяет выявить наиболее эффективные стратегии и методы управления, а также определить оптимальные параметры системы.

Таким образом, математическая модель является мощным инструментом в управлении, который помогает принимать обоснованные решения, оптимизировать процессы и достигать поставленных целей. Ее использование позволяет управляющим оперировать объективными данными, учитывать множество факторов и вариантов развития ситуаций, а также проводить анализ и эксперименты для оптимизации управленческих процессов.

Основные принципы построения математической модели

1. Упрощение реальности: Любая математическая модель является упрощенным отображением действительности. В процессе построения модели необходимо выбрать те аспекты реальности, которые являются наиболее существенными для решаемой задачи.
2. Формализация: Математическая модель должна быть описана с помощью строго определенных математических символов и формул. Формализация позволяет установить ясные связи между различными переменными и параметрами модели.
3. Проверка: Построенную модель необходимо проверить на соответствие реальности. Проверка может быть осуществлена путем сравнения результатов моделирования с экспериментальными данными или с уже существующими математическими моделями.
4. Прогнозирование: Основной целью построения математической модели является возможность прогнозирования поведения системы в будущем. Модель должна быть способна предсказывать результаты при различных условиях и параметрах.
5. Гибкость и адаптивность: Математическая модель должна быть гибкой и адаптивной к изменениям внешних условий и параметров. Она должна позволять легко изменять параметры модели и анализировать их влияние на результаты.

Соблюдение данных принципов позволяет создавать надежные и эффективные математические модели, которые могут быть использованы для анализа и управления различными процессами и системами.

Вопрос-ответ:

Что такое математическая модель управления?

Математическая модель управления — это абстрактная математическая конструкция, которая описывает процесс управления и позволяет прогнозировать его результаты.

Какие принципы лежат в основе математической модели управления?

Основными принципами математической модели управления являются формализация, абстракция, моделирование и оптимизация.

Какая роль математической модели в управлении организацией?

Математическая модель позволяет организации более эффективно управлять своими ресурсами, прогнозировать результаты принимаемых решений и оптимизировать процессы.

Каким образом математическая модель управления помогает прогнозировать результаты?

Математическая модель управления использует данные о прошлых событиях и подразумевает наличие некоторых зависимостей между переменными, позволяя прогнозировать результаты будущих событий на основе этих зависимостей.

Какие примеры математических моделей управления существуют?

Примерами математических моделей управления являются модели экономического роста, модели логистической системы, модели управления запасами и другие.

Преимущества использования математической модели

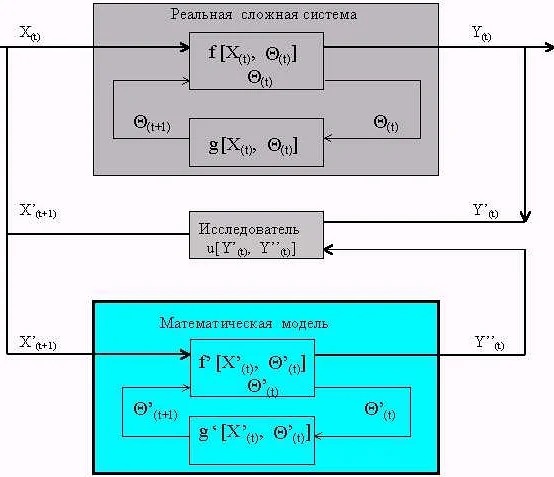
Использование математической модели в управлении предоставляет ряд преимуществ, которые делают этот подход эффективным и востребованным в различных областях. Ниже перечислены основные преимущества использования математической модели:

1. Точность предсказаний: математическая модель позволяет более точно предсказывать результаты действий и принимать решения на основе данных исторических и текущих данных. Это помогает снизить риски и улучшить результаты управления.
2. Оптимизация: математическая модель позволяет искать оптимальные решения в сложных ситуациях, где количество вариантов и ограничений является большим. Модель может учитывать различные факторы и находить наилучшие варианты, что помогает сделать более эффективные и экономически выгодные решения.
3. Прогнозирование: математическая модель позволяет прогнозировать различные сценарии развития событий на основе имеющихся данных. Это помогает предусмотреть возможные проблемы и предотвратить их, а также спланировать будущие действия и принять меры заранее.
4. Автоматизация: математическая модель может быть автоматизирована и внедрена в компьютерные системы, что позволяет обрабатывать большие объемы данных и принимать решения в реальном времени. Это упрощает и ускоряет процесс управления и улучшает его результаты.
5. Анализ и интерпретация: математическая модель позволяет анализировать и интерпретировать сложные данные, выявлять закономерности и тенденции, а также находить скрытые взаимосвязи между различными факторами. Это помогает лучше понять ситуацию и принимать более обоснованные решения.

В целом, использование математической модели в управлении позволяет повысить эффективность и результативность деятельности, снизить риски и принимать обоснованные решения на основе объективных данных и анализа.

Примеры применения математической модели в управлении

1. Управление производственными процессами: с помощью математической модели можно оптимизировать рабочие процессы, учитывая различные факторы, такие как количество ресурсов, время выполнения задач, распределение рабочих мест и другие параметры. Это позволяет увеличить эффективность производства и снизить издержки.
2. Управление логистическими системами: математическая модель может быть использована для оптимизации логистических процессов, таких как планирование маршрутов доставки, управление запасами и оптимизация распределения ресурсов. Это позволяет снизить время доставки, улучшить качество обслуживания и сократить расходы на логистику.
3. Управление финансовыми ресурсами: математическая модель может быть использована для прогнозирования финансовых показателей и оптимизации использования финансовых ресурсов. Например, с ее помощью можно определить оптимальные инвестиционные стратегии или рассчитать риск и доходность портфеля инвестиций.
4. Управление транспортными системами: математическая модель может быть использована для оптимизации работоспособности транспортной системы, такой как планирование маршрутов, управление потоками транспорта и расчет оптимального расписания.
5. Управление экологическими системами: математическая модель может быть использована для моделирования и анализа экологических систем, таких как изменение климата, распространение популяций животных или распределение растительности. Это позволяет оценивать влияние различных внешних факторов и принимать меры для снижения негативного воздействия на окружающую среду.

Применение математической модели в управлении позволяет повысить эффективность и точность принимаемых решений, а также снизить риски и издержки. Это делает ее незаменимым инструментом для управления сложными процессами и системами.

Ограничения и осложнения при создании математической модели

Одним из основных ограничений является упрощение реальности. Математическая модель представляет собой абстракцию реальной системы, и в процессе ее создания приходится делать определенные упрощения. Это может привести к потере некоторых деталей и особенностей реальной системы, что может сказаться на точности модели.

Еще одним ограничением является необходимость учета всех факторов и переменных, которые могут влиять на модель. В реальной системе может быть множество факторов, которые нужно учесть при создании математической модели. Однако, не всегда возможно учесть все эти факторы и переменные из-за ограниченности данных или сложности их учета.

Кроме того, при создании математической модели могут возникать проблемы с разрешимостью и вычислительной сложностью. Некоторые модели могут быть сложными в вычислительном смысле, что требует больших вычислительных ресурсов и времени для их решения. Также могут возникать проблемы с разрешимостью модели, когда не удается найти аналитическое решение или существует множество возможных решений.

Важно учитывать эти ограничения и осложнения при создании математической модели управления. Необходимо стремиться к балансу между точностью модели и ее вычислительной сложностью, а также учитывать все факторы и переменные, которые могут оказывать влияние на модель. Только так можно создать надежную и эффективную математическую модель управления.

Требования к качеству математической модели управления

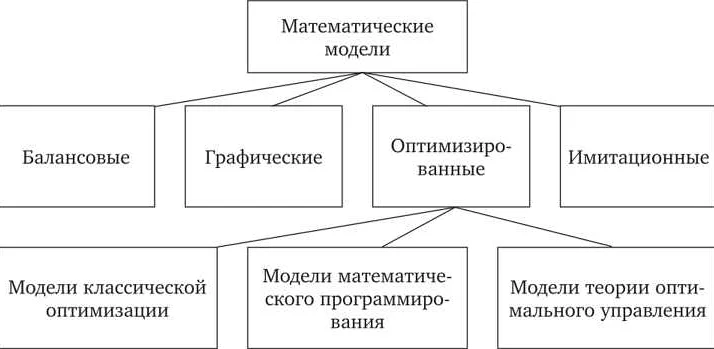
1. Адекватность модели.

Модель должна достоверно отображать основные характеристики и свойства системы, которую она описывает. Она должна быть способна точно предсказывать поведение системы в различных ситуациях.

2. Понятность и простота.

Модель должна быть понятной и простой для использования и интерпретации. Люди, не имеющие специализированного математического образования, должны быть способны понять модель и ее результаты.

3. Проверяемость и верифицируемость.

Модель должна быть проверяемой и верифицируемой. Это означает, что ее результаты должны быть подтверждены реальными экспериментами или наблюдениями.

4. Гибкость и адаптируемость.

Модель должна быть гибкой и адаптивной к изменениям в системе. Она должна быть способна учитывать различные факторы и условия, которые могут влиять на систему и ее управление.

5. Эффективность и точность.

Модель должна быть эффективной и точной. Она должна обладать достаточной точностью для анализа и прогнозирования поведения системы, а также быть вычислительно эффективной для обработки больших объемов данных.

6. Устойчивость.

Модель должна быть устойчивой к возможным возмущениям и погрешностям входных данных. Она должна сохранять свою работоспособность и точность даже при небольших изменениях в системе.

Удовлетворение требованиям к качеству математической модели управления является важным условием для ее успешного применения в практике управления и принятия решений.

Процесс создания математической модели управления

Первый этап — определение целей и задач управления. Необходимо понять, какие параметры системы нужно управлять, какие критерии оптимальности должны быть достигнуты.

Второй этап — определение структуры модели. На этом этапе определяются переменные и параметры модели, а также связи между ними.

Третий этап — определение уравнений модели. На основе знания физических законов и принципов работы системы формулируются уравнения, которые описывают динамику системы.

Четвертый этап — оценка и анализ модели. Модель должна быть проверена на соответствие реальной системе и проанализирована на предмет достижения поставленных целей управления.

Пятый этап — использование модели для управления. Математическая модель может быть использована для создания алгоритмов управления и принятия решений в реальном времени.

Таким образом, процесс создания математической модели управления включает в себя определение целей и задач управления, определение структуры и уравнений модели, а также ее оценку и использование для управления системой.