Этапы математического моделирования: как построить точную модель

Статья рассказывает о том, на сколько этапов обычно делится математическое моделирование, какие методы используются на каждом этапе и как важно тщательно продумать каждый этап для достижения качественного результата.

Математическое моделирование является одним из основных инструментов в современной науке и технике. С его помощью можно описать и предсказать поведение различных систем, от экономики до биологии. Однако, для создания точной математической модели необходимо пройти ряд этапов, которые мы и рассмотрим в этой статье.

Первый этап – формулирование задачи. Как и в любой научной деятельности, необходимо четко определить, что мы хотим получить в результате математического моделирования. Задача должна быть четко поставлена, иметь конкретные параметры и измерения, а также указывать на цели исследования.

Второй этап – моделирование. На этом этапе выбирается математический метод, который будет использоваться для создания модели. Также определяются переменные и параметры, которые будут входить в модель, а также их взаимосвязи. Для уточнения модели могут использоваться численные методы и компьютерные программы.

Третий этап – исследование созданной модели. На этом этапе проводятся анализ результатов, их интерпретация и точность. Если модель не отвечает поставленным требованиям, то необходимо внести коррективы или создать новую модель.

И, наконец, четвертый этап – использование полученных результатов. В зависимости от поставленной задачи, результаты использоваться могут в различных областях, от разработки новых технологий до управления продажами и бизнес-стратегиями.

Что такое математическое моделирование

Математическое моделирование — это метод решения проблем путём создания абстрактных математических моделей явлений реального мира. Понятие модели предполагает, что в создаваемом описании существенные свойства реального объекта сохраняются, а нерелевантные упрощаются.

Цель математического моделирования — предсказать поведение системы в различных условиях. Модели могут быть использованы для изучения уже произошедших событий, предсказания будущих событий и исправления нежелательных последствий. Математические модели широко используются в различных областях, таких как экономика, экология, физика, биология, социология.

Успешное моделирование требует создания математической концепции которая точно отражает поведение объекта. Модель должна быть проверена на предмет точности и соответствия реальности. Однако любая модель всегда лишена полной точности, так как не способна учесть все возможные факторы. Поэтому моделирование не является абсолютно точным, но оно позволяет предсказать поведение системы с высокой степенью вероятности.

Существует несколько методов математического моделирования, каждый из которых использует определенные инструменты и подходы для получения результата. Но все они базируются на принципах математики, статистики, алгебры, геометрии и других математических дисциплин. Надёжность, точность и достоверность обеспечиваются математическим методом, который гарантирует корректность решения задачи при определенных условиях.

Зачем нужно математическое моделирование

Математическое моделирование является незаменимым инструментом во многих научных областях, особенно в тех, где экспериментальное исследование невозможно или слишком дорого.

Модели позволяют исследовать сложные системы, предсказывать их поведение и оценивать эффективность различных стратегий. Также математические модели позволяют сэкономить время и ресурсы, которые были бы израсходованы на дорогостоящие и длительные эксперименты.

Математическое моделирование используются в разных областях науки и техники — от аэродинамики и физики до экономики и медицины. Одни из самых важных областей, где необходимость в математическом моделировании критически важна — это прогнозирование и предотвращение стихийных бедствий, климатических изменений, эпидемий и пандемий.

Таким образом, математическое моделирование является мощным инструментом, который помогает убедиться в правильности научных гипотез, прогнозировать поведение сложных систем, принимать решения на основе точных математических анализов и экономить деньги и время.

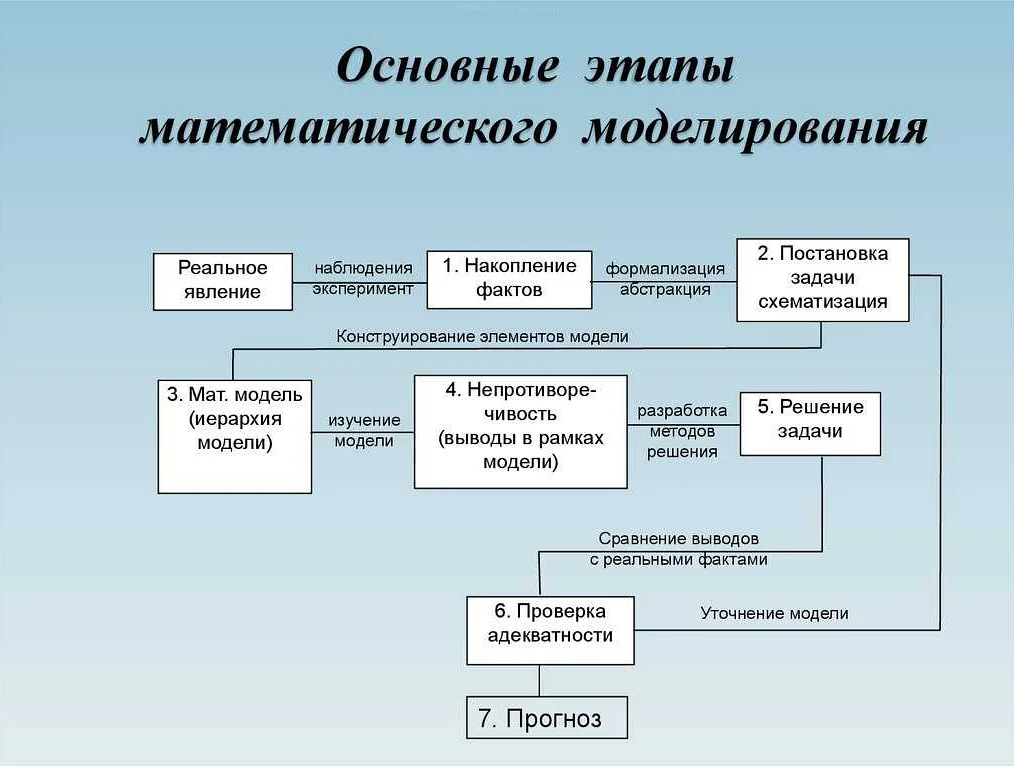
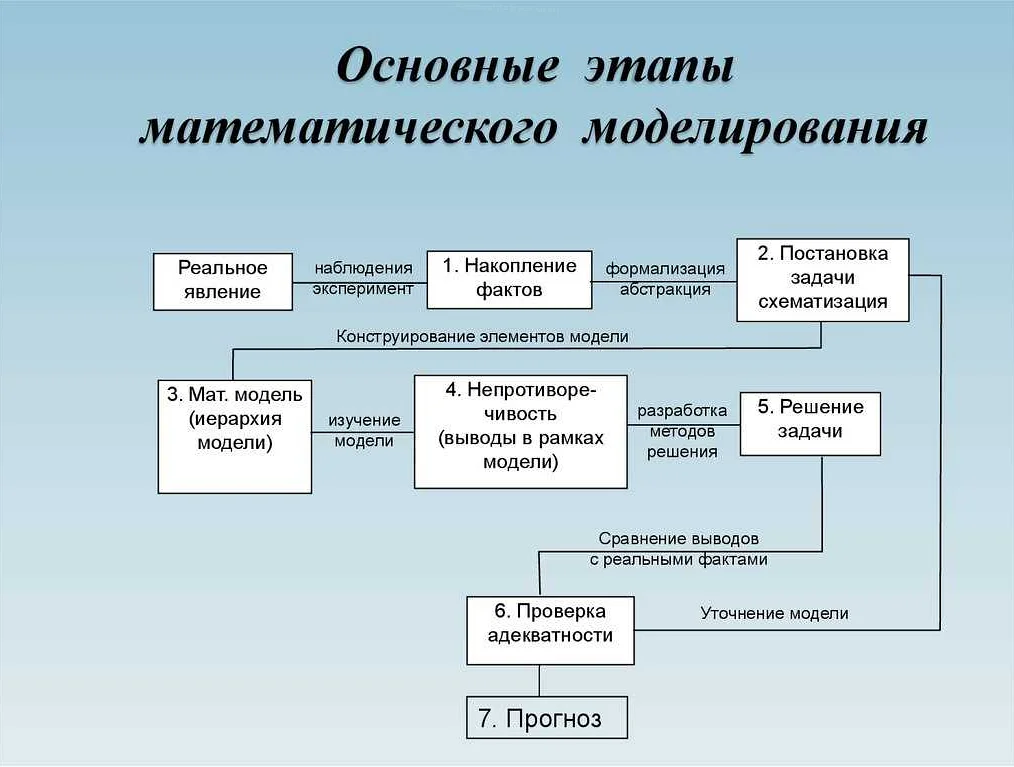
Этапы математического моделирования

Математическое моделирование — это процесс создания математических моделей, которые позволяют описывать и понимать реальные системы и процессы. Чтобы создать хорошую математическую модель, необходимо пройти ряд этапов, которые помогут создать точное и полное описание исследуемого явления.

1. Сбор данных.

Первый этап математического моделирования — сбор данных об исследуемом явлении. Важно получить максимально точную и полную информацию о системе, которую мы хотим изучить. Сбор данных включает в себя исследование литературы, наблюдения, эксперименты, опросы и т.д.

2. Формулирование гипотезы.

Второй этап — формулирование гипотезы о исследуемом явлении. Гипотеза — это предположение о том, как работает система. Она должна быть основана на данных, полученных на первом этапе, и позволяет определить, какие переменные влияют на систему и как они связаны друг с другом.

3. Разработка математической модели.

На третьем этапе создается математическая модель, которая описывает исследуемую систему. Модель может быть аналитической, численной или символической. Важно, чтобы модель была гибкой, чтобы ее можно было адаптировать под различные условия.

4. Определение области применимости.

Четвертый этап — определение области применимости модели. Модель может быть применима только в определенных условиях, поэтому важно определить, где она может быть использована, а где нет. Также на этом этапе проводятся проверки модели на пригодность и точность.

5. Проведение экспериментов и валидация модели.

Пятый этап — проведение экспериментов, чтобы проверить предсказания, которые даёт математическая модель. Валидация — это процесс проверки, насколько точно математическая модель описывает исследуемую систему. Если модель точна, её можно использовать для прогнозирования, управления, оптимизации и других целей.

6. Использование модели в практической деятельности.

Шестой этап — использование модели в практической деятельности. Модель может использоваться для предсказания различных сценариев и сделать прогнозы для решения реальных проблем. Она может быть применена в науке, промышленности, экономике, медицине и других областях.

Этап 1: Формулирование проблемы

Формулирование проблемы является первым и одним из самых важных этапов математического моделирования. На данном этапе необходимо понять, какая задача стоит перед нами и что нужно решить.

При формулировании проблемы необходимо определить, что именно будет моделироваться: процесс, система, объект. Здесь важно определить все главные параметры и элементы, которые будут участвовать в будущей математической модели.

Нередко при формулировании проблемы возникают вопросы, такие как: Что именно хотим достичь этой моделью? Какие ограничения и оговорки должны учитываться при создании модели? Насколько точно должна быть модель? Ответы на эти вопросы позволят сформулировать проблему грамотно и точно.

Чем точнее и полнее будет сформулирована проблема, тем эффективнее и быстрее будет выполнено следующее, более трудоемкое, этапы математического моделирования.

Основная цель этого этапа — понимание вопроса, который мы будем решать, и создание условий для более точного и продуктивного математического моделирования в будущем.

Этап 2: Выбор исходных данных

Выбор исходных данных — это очень важный этап математического моделирования, на котором определяются изначальные условия для создания математической модели. Эти данные должны быть точными и достоверными, иначе они могут привести к неверным результатам.

Чтобы правильно выбрать исходные данные, необходимо проанализировать их и оценить их качество. Исходные данные должны быть представлены в удобной для моделирования форме и легко доступны для обработки. Важно также учитывать ограничения, связанные с использованием этих данных и их точностью.

При выборе исходных данных следует также учитывать, что они должны отражать реальные условия и характеристики системы, которую необходимо моделировать. Важно также учитывать возможные изменения и колебания в этих условиях, чтобы модель могла учитывать эти факторы.

В процессе выбора исходных данных можно использовать различные методы, такие как опросы, экспертные оценки, анализ данных и другие источники. Важно также учесть, что некоторые данные могут быть недоступны из-за ограничений доступа или других причин. В этом случае необходимо использовать наиболее точные данные, которые доступны.

В итоге, правильный выбор исходных данных помогает создать точную и надежную математическую модель, которая может быть использована для анализа реальных процессов и принятия соответствующих решений.

Этап 3: Разработка математической модели

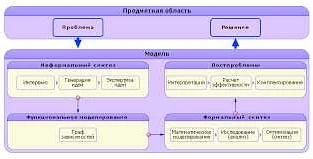
На данном этапе осуществляется разработка математической модели, которая позволяет описать функционирование объекта исследования. Для этого необходимо выбрать соответствующие математические методы и модели.

Модель может быть представлена в виде уравнений, систем уравнений или алгоритма. Важно учитывать, что модель должна отражать ключевые характеристики объекта исследования и быть подходящей для решения поставленной задачи.

Разработка математической модели требует глубокого понимания исследуемого объекта, а также точного и аккуратного описания его особенностей. Важно учитывать, что математическая модель может быть упрощенной или сложной в зависимости от поставленной задачи и доступных ресурсов для ее реализации.

Для успешного решения поставленной задачи необходимо проверять и уточнять разработанную модель, используя полученные результаты и экспериментальные данные. Этот этап также может включать обработку статистических данных и выполнение других расчетов.

В целом разработка математической модели является ключевым этапом в математическом моделировании, потому что от качества модели зависит решение поставленной задачи. Важно учитывать, что модель может быть уточнена и развита на следующих этапах моделирования.

Этап 4: Проведение эксперимента

На данном этапе мы проверяем полученную математическую модель на практике. Для этого проводим эксперимент, наблюдаем, измеряем и регистрируем результаты, а затем сравниваем их с предсказаниями модели.

Обычно эксперимент проводят несколько раз, чтобы убедиться в правильности модели и выявить ее ограничения. В случае, если результаты эксперимента не совпадают с предсказаниями модели, необходимо анализировать полученные данные и вносить коррективы в математическую модель.

Важно отметить, что эксперименты должны проводиться с учетом допущений, которые были сделаны на предыдущих этапах. Кроме того, необходимо учитывать вероятность возникновения случайных факторов, которые могут влиять на результаты эксперимента.

В итоге, успешное проведение экспериментов подтверждает правильность математической модели и позволяет использовать ее для решения практических задач в соответствующей области знаний.

Этап 5: Анализ результатов

После проведения моделирования и получения результатов необходимо проанализировать полученные данные. Важно определить точность модели и достоверность полученных результатов.

Сначала необходимо сравнить модельные результаты с реальными данными. Если модельные результаты существенно отличаются от реальных, необходимо проанализировать, какие условия и/или параметры не учитываются в модели.

Далее необходимо проанализировать влияние каждого параметра на результаты моделирования. Часто бывает так, что изменение одного параметра может значительно повлиять на конечный результат. Это необходимо учитывать при принятии решений на основе результатов моделирования.

Также необходимо проанализировать возможность применения модели на практике. Не все модели могут быть реализованы в реальном мире. Необходимо учитывать возможные ограничения и препятствия для реализации модели на практике.

Окончательный анализ результатов поможет сделать выводы о том, насколько точна и полезна модель, и какие рекомендации можно сделать на основе полученных результатов.

Этап 6: Валидация модели

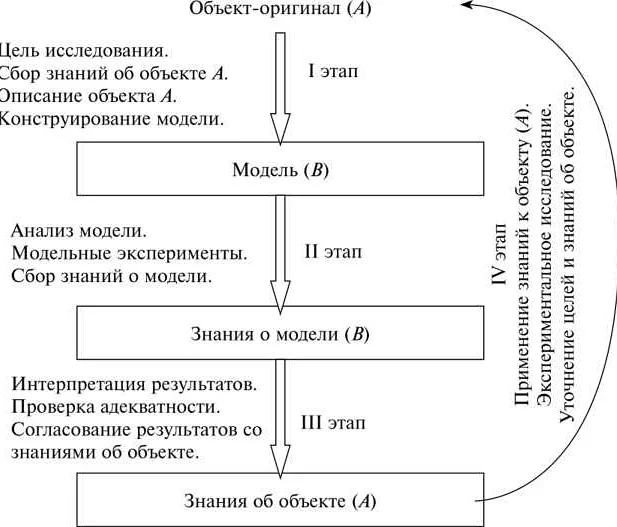
Предыдущие этапы моделирования включали в себя создание и разработку математической модели, ее решение и анализ результатов. Однако, полученные на этих этапах результаты не всегда являются достоверными и точными. Это связано с тем, что математическая модель является упрощенным отражением реальных процессов и явлений. Поэтому необходим этап валидации модели.

Валидация модели является процессом проверки соответствия результатов, полученных с помощью математической модели, реальным результатам. Этот этап позволяет оценить степень точности и достоверности модели.

Для валидации модели необходимо проводить эксперименты на объекте, который моделируется. Полученные на объекте результаты сравниваются с результатами, полученными с помощью математической модели. Если результаты соответствуют друг другу, то модель считается валидной.

Важно заметить, что в процессе валидации модели может произойти отклонение результатов на объекте от результатов, полученных с помощью математической модели. В этом случае необходимо провести анализ и определить причины отклонения. Может потребоваться доработка математической модели или введение дополнительных факторов.

Таким образом, валидация модели является важным этапом математического моделирования, который позволяет оценить точность и достоверность модели. Без проведения этого этапа результаты моделирования могут быть недостоверными и неинформативными.

Видео по теме:

Вопрос-ответ:

Что такое математическое моделирование и для чего оно используется?

Математическое моделирование — это метод исследования объекта путём сознательного построения математической структуры, которая является формальным описанием этого объекта или процесса. Оно используется в различных областях — от физики и химии до экономики и социологии — для того, чтобы прогнозировать поведение системы, анализировать её свойства и оптимизировать процессы.

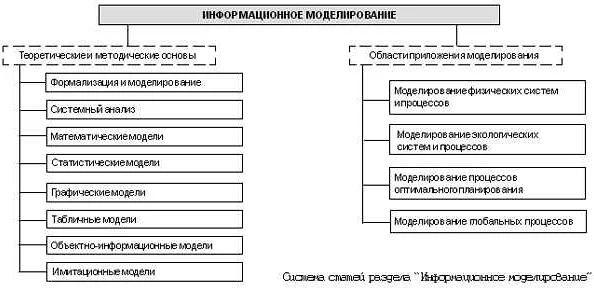
Какие этапы включает процесс математического моделирования?

Процесс математического моделирования включает несколько этапов: постановку задачи, формализацию (представление исходной проблемы в виде математических знаков и символов), построение модели (выбор типа модели, определение зависимостей, выбор методов описания), решение (поиск решения математической задачи), интерпретацию (сопоставление результата моделирования реальным данным), верификацию (проверку корректности модельных задач и сравнение результатов с экспериментальными) и валидацию (оценку точности моделирования и полученных результатов).

Какая роль формализации в процессе математического моделирования?

Формализация — это процесс перевода вещей и процессов в язык математики. Такое представление позволяет сформулировать проблему в терминах точных математических понятий и снижает вероятность неправильной интерпретации результатов. Она также упрощает процесс построения моделей, поскольку представление данных и знаний в языке математики позволяет использовать более точные методы вычислительной математики.

Как выбрать подходящий тип математической модели?

Выбор подходящего типа модели зависит от типа задачи, а также от доступности и качества данных. Если имеются хорошие и качественные данные, то можно использовать модели, основанные на точной математической теории, например, дифференциальных уравнениях. В случае, если данных мало или они смутные, можно выбрать эмпирические модели или упрощенные физические модели, которые основываются на знаниях эксперта.

Что такое верификация и валидация модели?

Верификация — это процесс проверки модели на соответствие заданным требованиям, корректность использования математических соотношений и выбор методов решения задачи. Валидация — это процесс сопоставления результатов моделирования с экспериментальными данными для оценки точности моделирования и её качества. Оба этапа важны, поскольку позволяют убедиться в корректности выбора и разработки модели, её применимости и адекватности.

Какие методы используют для решения математических моделей?

Для решения математических моделей используются различные методы — от аналитических до численных. Аналитические методы позволяют найти точное аналитическое решение задачи, если это возможно. Численные методы могут использоваться в тех случаях, где точное решение не может быть найдено или его поиск является слишком сложным и затратным по времени. К численным методами относятся методы конечных элементов, методы Монте-Карло, численные методы решения дифференциальных уравнений, методы оптимизации и другие.

Какая роль математического моделирования в современном мире?

Математическое моделирование играет важную роль в современном мире. Оно используется во многих областях, в том числе в науке, технике, экономике, социологии, медицине и экологии, для решения различных задач, от проектирования и оптимизации процессов до прогнозирования поведения системы в различных условиях. Благодаря математическому моделированию создаются новые технологии, улучшаются процессы производства, оптимизируются затраты, ведётся решение сложных задач и позволяет прогнозировать и контролировать процессы.

Этап 7: Калибровка модели

Калибровка модели — процесс, направленный на определение значений параметров модели и их соотношений, которые позволяют наилучшим образом описывать реальные данные и явления. Она является важным этапом математического моделирования, так как точность и эффективность работы модели зависят от правильности выбора параметров.

Для калибровки моделей нужны данные, собранные на реальных объектах или в лабораторных условиях. В процессе калибровки модели помогают различные инструменты, такие как статистические тесты, анализ данных и оптимизационные методы. Они позволяют определить наилучшие значения параметров в соответствии с реальными данными.

Калибровка модели может быть продуктивной только в том случае, если у модели есть достаточно точные и качественные данные. Если данные не соответствуют реальности, то необходимо производить модификацию самой модели или собирать новые данные для калибровки. Для наилучших результатов необходимо включать в калибровку как можно больше различных типов данных и показателей.

Важно отметить, что калибровка модели — это процесс, который может быть продолжительным и иметь множество итераций. Чем точнее и полнее результаты калибровки, тем более точными будут прогнозы, сделанные на основе этой модели.

Примеры математического моделирования в разных областях

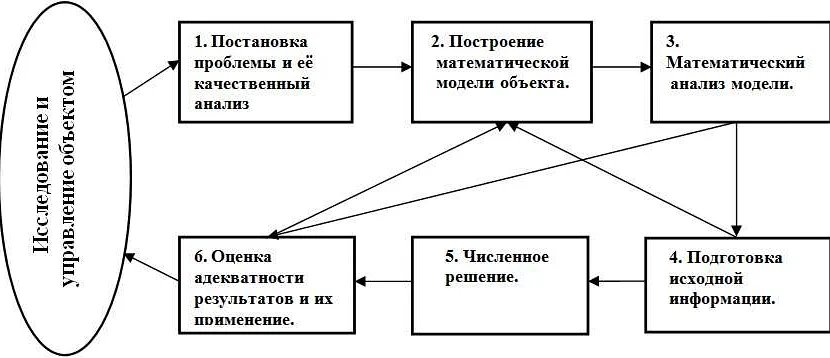
Физика

Математическое моделирование играет важную роль в физике для понимания свойств и поведения различных физических систем. Например, математические модели используются для моделирования движения тел в пространстве, электромагнитных волн, фотонных кристаллов и многих других физических явлений.

Медицина

В медицине математическое моделирование часто используется для описания биомеханики и физиологии человеческого тела, а также для моделирования различных заболеваний. Например, математические модели используются для изучения распространения инфекций, моделирования действия лекарственных препаратов и определения оптимальных доз.

Экономика

Математическое моделирование в экономике используется для прогнозирования развития экономических процессов и оценки эффективности экономических механизмов управления. Например, моделирование используется для анализа изменения цен на товары и услуги, ожидаемой прибыли, расчета оптимальных стратегий инвестирования и других задач.

Информационные технологии

В области информационных технологий математическое моделирование используется для создания и совершенствования алгоритмов, программ и искусственного интеллекта. Например, математические модели используются при создании компьютерных игр, распознавания образов, настройки рекомендательной системы и других задач.

Астрономия

Математическое моделирование в астрономии играет важную роль для изучения и предсказания движения небесных тел и исследования звездных систем. Например, математические модели используются для расчета траектории движения комет и метеорных потоков, прогнозирования погоды в космосе и других задач.

• В результате таких математических моделей можно более точно оценить риски, и снизить траты на неверные решения, а также оптимизировать результаты и ускорить время выполнения задач.