Что значит три этапа математического моделирования

Три этапа математического моделирования: формулировка задачи, построение модели и анализ результатов. Узнайте, каким образом математическое моделирование помогает понять сложные явления и принимать обоснованные решения.

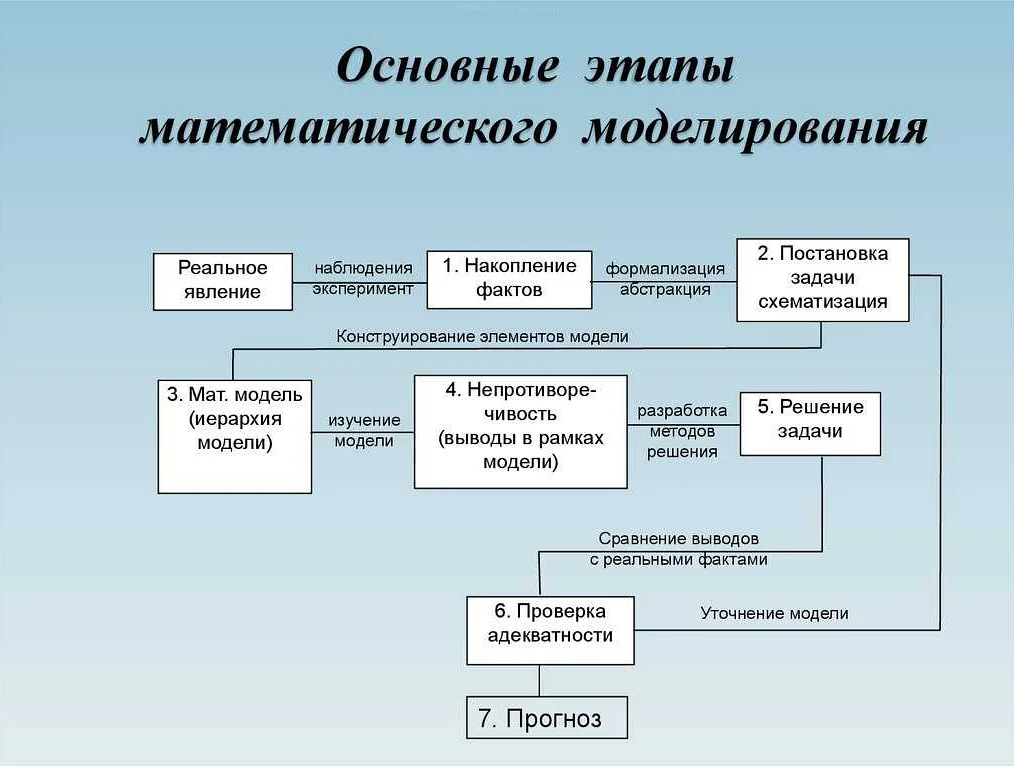
Математическое моделирование – это процесс создания абстрактной математической модели для изучения и анализа сложных систем или явлений. Все моделирование состоит из трех основных этапов: понимание сути проблемы, построение математической модели и анализ полученных результатов.

На первом этапе требуется полное понимание сути проблемы. Исследователь должен проанализировать все факторы, влияющие на систему, определить связи между ними и выявить основные закономерности. Это поможет сократить количество переменных и увеличить точность модели.

Второй этап – построение математической модели – является самым сложным и трудоемким. Здесь необходимо выбрать правильные математические уравнения, которые точно описывают систему или явление. При этом нужно учитывать все условия, ограничения и предположения, которые могут повлиять на результаты моделирования.

«Математическое моделирование – это процесс создания абстрактной математической модели для изучения и анализа сложных систем или явлений».

После построения математической модели наступает третий этап – анализ полученных результатов. Здесь исследователь анализирует полученные данные, выявляет закономерности, прогнозирует возможные сценарии развития и оценивает эффективность принятых решений. Важно отметить, что анализ результатов может привести к необходимости корректировки модели или получению дополнительных данных.

Значение и применение математического моделирования

Значение математического моделирования заключается в его способности упрощать сложные реальные ситуации и представлять их в виде формальных математических моделей. Это позволяет исследователям получить глубокое понимание сущности и особенностей изучаемых явлений.

Первый этап математического моделирования – понимание сути – предполагает анализ объекта и его характеристик, выявление причинно-следственных связей, определение важных факторов и переменных. Затем следует построение математической модели, которая представляет собой абстракцию реальности и описывает взаимосвязи между переменными.

Анализ результатов – последний этап моделирования – включает в себя решение уравнений модели, интерпретацию полученных данных и сравнение их с экспериментальными или наблюдаемыми данными. Это позволяет оценить точность модели и сделать выводы о ее применимости и полезности.

Применение математического моделирования широко распространено в различных областях. В науке, оно используется для изучения физических и химических процессов, биологических систем, социальных явлений и экономики. В технике, моделирование позволяет проектировать и оптимизировать различные устройства, системы и процессы. В экономике, моделирование помогает анализировать рыночные тенденции, прогнозировать экономические показатели и принимать решения в условиях неопределенности.

Таким образом, математическое моделирование играет важную роль в современном мире, обеспечивая научные исследования, инженерные разработки и принятие обоснованных решений в различных сферах деятельности.

Понимание сути математического моделирования

Первый этап математического моделирования — это понимание сути изучаемого явления. Он предполагает детальное изучение объекта и определение основных факторов, влияющих на его поведение. Важно учитывать все существенные аспекты и особенности, чтобы построить правильную модель.

На этом этапе исследователи используют различные методы анализа, такие как наблюдение, эксперимент, аналогии и теоретические рассуждения. Они анализируют существующие данные, изучают литературу и консультируются с экспертами в соответствующей области знаний.

Понимание сути моделирования также предполагает построение гипотез, которые позволяют сформулировать основные предположения и представления о взаимодействии факторов и возможных закономерностях. Это помогает установить начальные условия и параметры для моделирования.

Надлежащее понимание сути моделирования является фундаментальным шагом, который определяет качество и достоверность построенной модели. Оно позволяет исследователям определить, какие аспекты явления следует учитывать, а какие можно пренебречь. Это помогает сократить количество необходимых расчетов и снизить степень сложности модели.

В итоге понимание сути математического моделирования позволяет исследователям получить основу для дальнейшего построения более точных и эффективных моделей, а также анализировать и интерпретировать полученные результаты.

Этапы построения математической модели

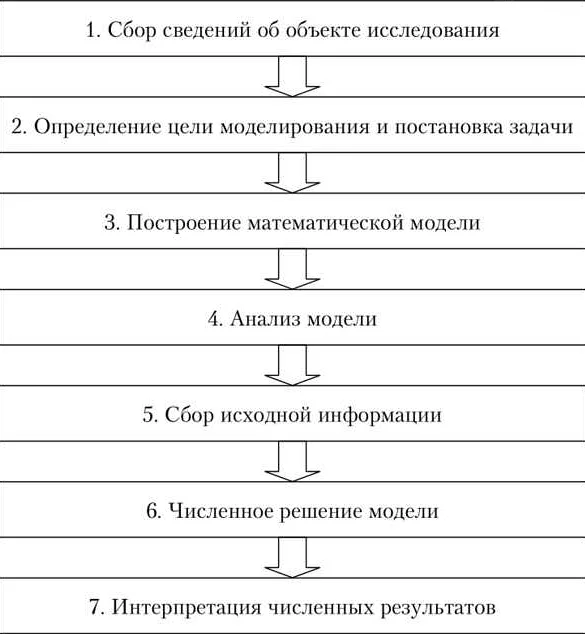
Первый этап – понимание сути. На этом этапе исследователь должен четко определить объект исследования и осознать, какие процессы и явления влияют на его функционирование. Для этого проводится анализ исходных данных, изучение литературы и консультации с экспертами в данной области. Цель этого этапа – получить полное представление о сущности исследуемого объекта.

Второй этап – построение модели. На этом этапе исследователь создает математическую формулу или систему уравнений, которые описывают взаимодействие различных факторов в рамках исследуемого объекта. Для этого используются математические методы и инструменты, такие как дифференциальные уравнения, статистические модели или оптимизационные задачи. Цель этого этапа – создать модель, которая наиболее точно отражает реальное поведение исследуемого объекта.

Третий этап – анализ результатов. На этом этапе исследователь анализирует полученные модельные данные и сравнивает их с реальными данными или с результатами других исследований. В результате анализа можно сделать выводы о соответствии модели реальности, а также о возможных способах улучшения модели. Цель этого этапа – оценить качество модели и предложить рекомендации для дальнейшего исследования или принятия решений.

Таким образом, построение математической модели включает три этапа: понимание сути, построение модели и анализ результатов. Каждый из этих этапов является важным и необходимым для достижения цели исследования и получения достоверных результатов.

Важность выбора адекватной модели

Адекватная модель должна корректно отражать реальную ситуацию или процесс, которые мы хотим изучить или описать. Она должна учитывать все существенные факторы, влияющие на исследуемую систему, и устанавливать их взаимосвязи. Важно помнить, что модель – это упрощенное представление сложной реальности, поэтому выбор модели должен основываться на глубоком понимании сути и особенностей исследуемого объекта.

Неправильный выбор модели может привести к искажению результатов и неправильному выводу о процессе или системе. Если модель слишком упрощена или не учитывает важные факторы, то ее результаты могут быть недостоверными. С другой стороны, если модель слишком сложна или содержит излишнюю информацию, то ее использование может быть затруднено или даже невозможно.

Поэтому перед построением модели необходимо провести анализ исходных данных, изучить свойства исследуемой системы, а также определить цель и задачи моделирования. На основе этих данных можно выбрать наиболее подходящий математический аппарат и построить адекватную модель.

Важность выбора адекватной модели заключается не только в получении точных результатов, но и в возможности использования модели для дальнейших исследований и принятия решений на основе полученных данных. Адекватная модель может стать мощным инструментом анализа и оптимизации, что позволит прогнозировать будущие события, находить оптимальные решения или предлагать различные стратегии действий.

В целом, выбор адекватной модели является основой для успешного математического моделирования и обеспечивает достоверность, точность и полезность получаемых результатов. Поэтому необходимо уделить достаточно времени и внимания на этапе выбора модели, чтобы гарантировать качество и эффективность всего процесса математического моделирования.

Первый этап: формализация проблемы

На этом этапе необходимо провести анализ исходных данных и определить, какие факторы являются ключевыми для решения проблемы. Затем формулируются математические условия, ограничения и целевые функции, которые будут использоваться в модели.

Важно, чтобы формализация проблемы была максимально точной и полной, чтобы модель корректно отражала реальность и позволяла проводить анализ и прогнозирование.

Второй этап: построение математической модели

Второй этап математического моделирования заключается в построении математической модели, которая описывает явление или процесс, подлежащий исследованию. На этом этапе осуществляется перевод сущностей и связей предметной области в математические термины и формулы.

Построение математической модели требует глубокого понимания сути и особенностей исследуемого явления. При этом необходимо определить базовые переменные и параметры, которые будут использоваться в модели. Также нужно выбрать математический аппарат, подходящий для описания и решения задачи.

На этом этапе также определяются граничные условия и начальные условия, которые задаются для решения математической модели. Граничные условия определяют значения переменных на границах модельной области, а начальные условия задают значения переменных в начальный момент времени.

После построения математической модели осуществляется ее формализация в виде уравнений и систем уравнений. Эти уравнения могут быть дифференциальными, интегральными или алгебраическими, в зависимости от природы исследуемого явления.

Важным этапом в построении математической модели является проверка ее адекватности и точности. Для этого проводятся сравнение результатов моделирования с реальными данными и экспериментальными результатами. Если модель достаточно точно описывает наблюдаемые явления, то она считается адекватной и может быть использована для анализа результатов и прогнозирования поведения системы в различных условиях.

Третий этап: анализ результатов моделирования

На третьем этапе математического моделирования происходит анализ полученных результатов. После построения математической модели и проведения необходимых расчетов, необходимо проанализировать полученные результаты и сделать выводы.

Во время анализа результатов моделирования, исследователь обращает внимание на важные особенности полученных данных. Он анализирует графики, таблицы и другие выходные данные модели, чтобы выявить закономерности и тенденции. Исследователь также может сравнивать результаты с реальными наблюдениями или другими моделями для проверки достоверности модели.

Важным аспектом анализа результатов является интерпретация данных. Исследователь должен понять, что означают полученные числа и графики в контексте изучаемой проблемы. Он может провести дополнительные расчеты или выделить основные тренды и закономерности для более глубокого понимания процесса или системы, которую он моделировал.

Кроме того, анализ результатов моделирования позволяет провести оценку точности модели. Исследователь может сравнивать результаты моделирования с экспериментальными данными или другими надежными источниками информации, чтобы определить, насколько точно модель отражает реальность. Если модель не соответствует ожиданиям, исследователь может вносить корректировки и улучшать модель для достижения более точных результатов.

Третий этап математического моделирования — анализ результатов — играет важную роль в использовании моделей для решения реальных проблем. Он предоставляет исследователю информацию и понимание, необходимые для принятия обоснованных решений и предсказания будущих событий или трендов. Анализ результатов помогает исследователю лучше понять систему, а также оценить надежность и полезность модели.

Видео по теме:

Вопрос-ответ:

Какие этапы включает в себя математическое моделирование?

Математическое моделирование включает в себя три основных этапа: понимание сути проблемы, построение математической модели и анализ результатов.

Что подразумевается под пониманием сути проблемы в математическом моделировании?

Понимание сути проблемы в математическом моделировании означает, что необходимо ясно определить, какие аспекты проблемы требуется рассмотреть, какие взаимодействия между ними существуют, и какие важные факторы следует учесть.

Какой основной целью является построение математической модели?

Основной целью построения математической модели является представление проблемы в виде математических уравнений, которые описывают ее основные свойства и отношения между различными переменными. Такая модель позволяет проводить анализ и исследования, которые могут помочь в понимании и решении проблемы.

Каким образом проводится анализ результатов в математическом моделировании?

Анализ результатов в математическом моделировании включает в себя проведение расчетов, проверку модели на соответствие реальным данным, а также интерпретацию полученных результатов с целью выявления закономерностей, тенденций и возможных решений проблемы.

Какие преимущества имеет использование математического моделирования в решении проблем?

Использование математического моделирования в решении проблем позволяет проводить анализ и исследования без необходимости проведения реальных экспериментов, что может быть дорого и затратно по времени. Кроме того, моделирование позволяет предсказывать результаты в различных условиях и проводить эксперименты с различными параметрами, что помогает в принятии обоснованных решений.

Какие этапы включает в себя математическое моделирование?

Математическое моделирование включает в себя три основных этапа: понимание сути проблемы, построение математической модели и анализ результатов этой модели.

Что подразумевается под пониманием сути проблемы при математическом моделировании?

Понимание сути проблемы включает в себя анализ задачи, определение ее основных характеристик и понимание целей, которые необходимо достичь. Этот этап позволяет определить параметры, учитываемые в математической модели, и выбрать подходящий метод моделирования.

Критерии эффективности и достоверности модели

Критерии эффективности модели позволяют оценить, насколько хорошо модель описывает и предсказывает реальные явления. Одним из ключевых критериев является сопоставление результатов моделирования с экспериментальными данными. Если модель даёт результаты, близкие к наблюдаемым значениям, это говорит о её эффективности.

Кроме того, важно проверить модель на различные сценарии и условия. Если модель дает стабильные и последовательные результаты при изменении входных данных, это также указывает на её эффективность.

Достоверность модели, в свою очередь, связана с её соответствием реальности и точностью предсказаний. Одним из критериев достоверности модели является её способность объяснить наблюдаемые явления и зависимости между ними. Если модель представляет собой упрощенную версию реальности, она может быть недостоверной.

Также важно проверить модель на предсказательную силу. Если модель может предсказывать будущие состояния или события, это говорит о её достоверности.

Оценка эффективности и достоверности модели является неотъемлемой частью математического моделирования. Без этой оценки необходимо быть осторожными в использовании результатов моделирования для принятия решений и делать дополнительные проверки и анализы.

Примеры успешного математического моделирования

ОбластьПример моделиРезультаты

Экономика	Модель рыночной конкуренции	Позволила предсказать изменения цен и объемов продаж
Метеорология	Модель погоды	Позволяет предсказывать погодные условия и способствовать разработке стратегий для их управления
Медицина	Модель распространения инфекционных заболеваний	Позволяет оценивать эффективность программ вакцинации и контроля за распространением болезней
Транспорт	Модель движения автомобилей	Позволяет оптимизировать потоки транспорта и улучшить безопасность дорожного движения

Приведенные примеры показывают, что математическое моделирование является мощным инструментом для анализа комплексных систем и принятия обоснованных решений. Оно позволяет предсказывать результаты и оптимизировать процессы в различных областях деятельности.