Что входит в математическую основу карт

Математическая основа карт включает в себя геометрические принципы, проекции, координатные системы и алгоритмы, которые позволяют представить географическую информацию в виде карты. Узнайте, какие основные математические концепции используются при создании карт и как они влияют на точность и качество представления данных.

Карты являются неотъемлемой частью нашей жизни и используются в различных областях: от навигации и географии до анализа данных и визуализации информации. Однако, мало кто задумывается о том, каким образом карты создаются и какова их математическая основа.

Математическая основа карт включает в себя несколько ключевых аспектов. Во-первых, это геодезическая система координат, которая позволяет определить местоположение объектов на земной поверхности. Координаты определяются широтой, долготой и высотой.

Во-вторых, для создания карт используются различные проекции, которые позволяют отобразить трехмерную поверхность Земли на плоскость. Каждая проекция имеет свои преимущества и недостатки и выбирается в зависимости от целей и задач картографии.

Кроме того, создание карт связано с обработкой больших объемов данных, включающих географическую информацию. Для анализа и визуализации этих данных используются различные алгоритмы и методы, такие как кластеризация, градиентный спуск и интерполяция.

Основы математики в картографии

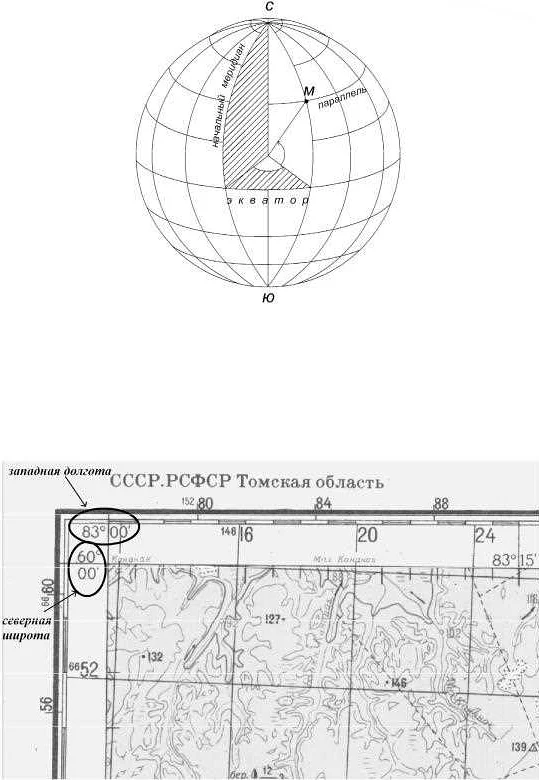
Одним из основных математических понятий в картографии является геометрия. Геометрические принципы позволяют определить форму и размеры земной поверхности, а также ее отображение на плоскости карты. Важные концепции в геометрии картографии включают проекции, координатные системы и масштабы.

Проекции – это методы преобразования трехмерной поверхности Земли в двухмерное изображение на карте. Существует множество различных проекций, каждая из которых имеет свои преимущества и недостатки. Проекции могут быть конформными (сохраняющими форму), эквидистантными (сохраняющими расстояния) или компромиссными (сочетающими оба качества).

Координатные системы используются для определения точного положения объектов на карте. Они позволяют задать координаты (широту и долготу) для каждой точки на поверхности земли. Наиболее распространенной системой координат является географическая система координат, которая использует широту и долготу.

Масштабы – это соотношения между расстояниями на карте и соответствующими расстояниями на земле. Они позволяют определить, насколько увеличена или уменьшена область на карте по сравнению с реальным миром. Масштабы могут быть выражены числовыми значениями (например, 1:10000) или графически.

В картографии также используются математические методы для обработки данных, создания моделей и проведения анализа. Это включает в себя решение геометрических задач, вычисления расстояний и площадей, а также анализ пространственных данных.

Таким образом, понимание основ математики в картографии играет важную роль в создании точных карт и анализе пространственной информации.

Видео по теме:

История создания карт и их математическая основа

Математическая основа карт состоит из нескольких важных компонентов. Одним из них является система координат, которая позволяет определить местоположение точек на карте. Наиболее распространенной системой координат является географическая система координат, основанная на широте и долготе.

Другим важным элементом математической основы карт является проекция. Проекция — это способ преобразования трехмерной поверхности Земли на плоскость карты. Существует множество различных проекций, каждая из которых имеет свои преимущества и ограничения.

Также математическая основа карт включает в себя использование масштаба. Масштаб показывает отношение между реальными размерами объектов на Земле и их изображениями на карте. Обычно масштаб выражается в виде числового соотношения или в виде графической шкалы.

Кроме того, в создании карт используются различные методы геоинформатики, которые позволяют собирать, обрабатывать и анализировать географическую информацию. Эти методы включают в себя геодезию, геоинформационные системы (ГИС) и др.

В целом, математическая основа карт играет важную роль в создании точных и надежных карт, которые являются неотъемлемой частью современного мира и используются в самых различных областях, от навигации до научных исследований.

Геодезические системы координат

Одной из наиболее распространенных геодезических систем координат является глобальная система координат WGS84 (World Geodetic System 1984). Она используется в GPS и других глобальных навигационных системах. В WGS84 широта измеряется в градусах от -90 до 90, долгота измеряется в градусах от -180 до 180, а высота над уровнем моря измеряется в метрах.

Внутри страны могут использоваться другие геодезические системы координат, такие как ПЗ-90 (Параметры Земли 1990 года) в России. Эти системы координат могут иметь свои особенности, такие как отличия в начальных точках или единицах измерения. Они позволяют более точно определить местоположение внутри страны.

Геодезические системы координат играют ключевую роль в создании и использовании карт. Они позволяют точно определить местоположение объектов на Земле и разместить их на карте. Без геодезических систем координат было бы невозможно создать точные и надежные карты, которые мы используем ежедневно для навигации и планирования.

Вопрос-ответ:

Какие математические основы лежат в основе создания карт?

Математические основы карт включают в себя геометрию, топологию и графы. Геометрия используется для определения размеров и форм карты, топология помогает определить связи между объектами на карте, а графы используются для построения путей и маршрутов.

Какие алгоритмы используются для построения карт?

Для построения карт используются различные алгоритмы, такие как алгоритмы растровой графики для отображения объектов на карте, алгоритмы поиска кратчайшего пути для навигации, алгоритмы сжатия данных для хранения карты в компактном формате и многие другие.

Как работает алгоритм поиска кратчайшего пути на карте?

Алгоритм поиска кратчайшего пути на карте основан на графовой теории. Он строит граф, где вершины представляют местоположения на карте, а ребра представляют возможные пути между этими местоположениями. Затем алгоритм находит кратчайший путь от начальной точки до конечной, используя различные стратегии, такие как алгоритм Дейкстры или алгоритм A*.

Каким образом используется топология в создании карт?

Топология используется для определения связей и отношений между объектами на карте. Например, топология может определить, что дом на карте находится рядом с дорогой, а не просто на одной и той же координате. Топология также может определить, какие объекты на карте связаны друг с другом, и использовать эту информацию для создания маршрутов и путей.

Какие проблемы могут возникнуть при построении и использовании карт?

При построении и использовании карт могут возникнуть различные проблемы. Некоторые из них включают в себя неточности в данных, ошибки в геометрии или топологии, проблемы с масштабированием карты, сложности в обработке больших объемов данных и трудности в оптимизации процесса отображения карты на устройствах с ограниченными ресурсами.

Проекции карт и их классификация

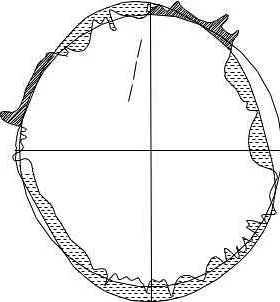
Проекции карт можно классифицировать по различным признакам. Одним из основных признаков является способ переноса географических объектов на плоскость. Существуют эквидистантные проекции, в которых сохраняется равенство масштаба на всей карте. Такие проекции часто используются для создания топографических карт.

Еще одним типом проекций являются равноугольные проекции, в которых сохраняется равенство углов. Это позволяет сравнивать направления и измерять углы на карте с высокой точностью. Такие проекции широко применяются в навигации и геодезии.

Также проекции карт можно классифицировать по зонам, в которых они наиболее точно отображают поверхность Земли. Например, существуют проекции, при которых зона наибольшей точности находится в тропиках или на полюсах.

Классификация проекций карт является сложной задачей, так как каждая проекция имеет свои преимущества и недостатки, которые зависят от цели ее использования и региона, который она отображает. Поэтому при выборе проекции необходимо учитывать конкретные условия и требования карто-графической работы.

Геодезические измерения и расчеты

Геодезические измерения включают в себя использование различных инструментов и методов для определения географических координат точек на поверхности Земли. Эти измерения позволяют создавать карты с высокой степенью точности и масштабирования.

Расчеты в геодезии включают в себя обработку полученных измерений и преобразование их в удобную форму для создания карты. Это включает в себя определение расстояний, углов, площадей и других характеристик географических объектов.

Для проведения геодезических измерений и расчетов используются различные математические методы, включая тригонометрию, геометрию, астрономию и гравиметрию. Эти методы позволяют учесть такие факторы, как кривизна Земли, силы притяжения и вращение Земли.

Важным аспектом геодезических измерений и расчетов является учет систем координат. Существует несколько систем координат, которые используются в геодезии, включая географические координаты (широта и долгота), прямоугольные координаты (плоская проекция) и высоты над уровнем моря.

Геодезические измерения и расчеты играют важную роль в создании карт и географических информационных систем. Они позволяют нам получать точные и надежные данные о мире, что помогает нам лучше понять и взаимодействовать с нашей планетой.

Топология на картах и ее роль

Топология на картах используется для определения различных географических свойств и атрибутов объектов на карте. Она позволяет анализировать и представлять пространственные данные с помощью геометрических отношений, таких как смежность, принадлежность, расстояние и направление.

Роль топологии на картах состоит в том, чтобы обеспечить точность и надежность географической информации на карте. Она позволяет проводить различные геоаналитические исследования, такие как определение путей, построение маршрутов, анализ сетей и многое другое.

Кроме того, топология позволяет решать проблемы, связанные с пересечением и слиянием геометрических объектов на карте. Она обеспечивает целостность данных и позволяет избежать ошибок при обработке и анализе географической информации.

Топология на картах имеет широкий спектр применений, включая геоинформационные системы, навигационные системы, геоаналитические исследования, планирование городской инфраструктуры и многое другое. Она является неотъемлемой частью математической основы карт и играет важную роль в анализе и представлении географической информации.

Математические методы для представления рельефа на картах

Одним из методов является использование изолиний. Изолинии представляют собой линии, соединяющие точки с одинаковой высотой над уровнем моря. Эти линии позволяют визуально представить рельеф и его изменения на карте.

Другим методом является применение теней. С помощью математических алгоритмов и данных о источнике света можно создать эффект объемности и глубины на карте. Такие тени позволяют более точно передать трехмерную структуру местности.

Также используются методы рельефной окраски и штриховки. При этом различным цветам или штриховкам присваиваются определенные высоты, что позволяет легко определить высотные зоны на карте.

Дополнительно к этим методам, существуют и другие математические подходы, такие как методы, основанные на фракталах и регулярных сетках. Все эти методы позволяют представить рельеф на карте с высокой точностью и детализацией.

• Метод изолиний
• Метод теней
• Метод рельефной окраски и штриховки
• Методы, основанные на фракталах и регулярных сетках

Каждый из этих методов имеет свои преимущества и недостатки, поэтому выбор конкретного метода зависит от целей и требований картографического проекта.

Использование математических моделей для прогнозирования изменения картографических данных

Математические модели могут представлять собой уравнения, алгоритмы или статистические методы, которые анализируют существующие картографические данные и на их основе строят прогнозы о возможных изменениях. Например, модель может использовать географические данные о рельефе, климате, гидрологии и других факторах, чтобы предсказать изменения ландшафта в будущем.

Прогнозирование изменений картографических данных может быть полезным для различных целей. Например, оно может быть использовано в геологии для прогнозирования геологических процессов, таких как извержения вулканов или землетрясения. Также математические модели могут помочь предсказать изменения в границах стран или национальных территорий, что может быть полезно для политического анализа.

Важно отметить, что прогнозы, полученные с помощью математических моделей, не всегда являются точными и должны быть подтверждены реальными наблюдениями и измерениями. Однако, использование математических моделей позволяет получить предварительные оценки и прогнозы, которые могут быть полезными для планирования и принятия решений.

Роль компьютерных технологий в математической основе картографии

Современная картография не обходится без компьютерных технологий, которые играют важную роль в создании и анализе карт. Они позволяют обрабатывать и анализировать огромные объемы географических данных, использовать сложные математические модели и алгоритмы для создания и отображения карт.

Компьютерные технологии позволяют проводить геоматический анализ данных, что включает в себя обработку и анализ пространственных данных, таких как координаты, высоты, формы и атрибуты объектов на карте. С помощью математических моделей и алгоритмов компьютеры могут строить различные типы карт, включая топографические, тематические, климатические карты и многие другие.

Компьютерные технологии также позволяют использовать географические информационные системы (ГИС) для создания и хранения картографических данных. ГИС позволяют интегрировать разные типы данных, проводить пространственный анализ и визуализацию информации на картах. Благодаря ГИС можно создавать интерактивные карты, на которых пользователи могут взаимодействовать с данными и получать дополнительную информацию.

Компьютерные технологии также играют важную роль в создании и обновлении цифровых карт, которые могут быть использованы в навигационных системах, мобильных приложениях и других технологиях. Они позволяют создавать детализированные и точные карты, которые могут быть обновлены в реальном времени и адаптированы под разные потребности пользователей.

Использование компьютерных технологий в картографии позволяет сделать карты более доступными, точными и интерактивными. Они значительно упрощают процесс создания карт, анализа данных и визуализации информации. Компьютерные технологии позволяют нам лучше понять и использовать географическую информацию, делая картографию более полезной и эффективной в различных областях деятельности.