Что такое проекция в математике

Проекция в математике — это процесс отображения объектов или пространственных фигур на плоскость или другое подпространство. Это важное понятие в геометрии, графике, анализе и других областях математики. Узнайте, как работает проекция и как ее применять в решении различных задач.

Проекция – это одно из фундаментальных понятий в математике, которое широко применяется в различных областях науки и техники. Оно позволяет описать связь между объектами в трехмерном пространстве и их изображениями на плоскости. Проекция используется для анализа и визуализации сложных геометрических объектов, а также для решения практических задач, связанных с конструированием и проектированием.

Проекция может быть определена как изображение объекта на плоскость, получаемое путем опускания перпендикуляра из каждой точки объекта на плоскость проекции. Результатом проекции является новый объект, который называется проекцией и обладает теми же геометрическими свойствами, что и исходный объект.

Проекции могут быть различных типов, в зависимости от способа, которым осуществляется проецирование. Наиболее часто используемыми являются ортогональные проекции, которые представляют собой проекции, осуществляемые параллельно определенным осям. Они позволяют получить изображение объекта на плоскости, сохраняя при этом его форму и размеры.

Например, ортогональные проекции широко применяются в архитектуре и инженерии для создания чертежей и планов зданий и сооружений. Они позволяют визуализировать объекты в двумерном виде, делая их более понятными для анализа и расчетов.

Определение проекции в математике

Проекции широко применяются в различных областях математики, физики, геометрии, компьютерной графики и других наук. Они позволяют упростить сложные пространственные конструкции и решать задачи, связанные с изображением, моделированием и анализом объектов.

Примером проекции может служить проецирование точек на плоскость с помощью перпендикулярных линий или параллельных лучей. Также известны и другие типы проекций, такие как центральная проекция, радиальная проекция, параллельная проекция и прочие.

Видео по теме:

Примеры проекции в математике

Вот несколько примеров проекций, которые широко применяются в математике:

ПримерОписание

Плоская проекция на оси координат	Это самый простой тип проекции, при котором объект проецируется на плоскость, параллельную осям координат. Эта проекция широко используется в графике и компьютерной графике для отображения двумерных данных.
Проекция на плоскость	Это проекция, при которой объект проецируется на плоскость, не обязательно параллельную осям координат. Примером такой проекции может быть проекция трехмерного объекта на двумерную поверхность.
Проекция на вектор	Это проекция, при которой объект проецируется на вектор — направленный отрезок. Проекция на вектор часто используется в линейной алгебре для вычисления компонентов вектора.
Проекция на плоскость вращения	Это проекция, при которой объект проецируется на плоскость, являющуюся плоскостью вращения. Проекция на плоскость вращения используется, например, для создания изображений трехмерных объектов с помощью фотографии или видео.

Это только некоторые из примеров проекций, которые применяются в математике. Проекции играют важную роль во многих областях, включая геометрию, графику, физику и многие другие.

Геометрическая интерпретация проекции

Проекция в математике имеет геометрическую интерпретацию, которая позволяет визуализировать этот математический объект. Она используется в геометрии, физике, инженерии и других отраслях науки.

Геометрическая интерпретация проекции связана с понятием перпендикулярности. Проекция точки на прямую представляет собой перпендикуляр, опущенный из этой точки на прямую. Таким образом, проекция точки на прямую является её «отражением» относительно этой прямой.

Проекция вектора на плоскость представляет собой вектор, который перпендикулярен этой плоскости и имеет такую же длину и направление, как исходный вектор. Это значит, что проекция вектора на плоскость показывает, какая часть исходного вектора лежит в этой плоскости.

Геометрическая интерпретация проекции позволяет легче понять и визуализировать проекции в математике. Она используется для решения задач в геометрии, анализе и других областях, где проекции играют важную роль.

Примеры проекций

Проекция точки на ось координат

Проекция вектора на плоскость

Проекция объекта на экран

Вопрос-ответ:

Что такое проекция в математике?

В математике проекция — это отображение точек или объектов на плоскость или пространство. Она используется для упрощения геометрических задач и анализа различных объектов.

Какие существуют примеры проекций в математике?

Примерами проекций в математике могут быть проекция точки на прямую, проекция точки на плоскость, проекция прямой на плоскость и т. д. Каждый из этих примеров имеет свои особенности и применяется в различных областях.

Как можно вычислить проекцию точки на прямую?

Для вычисления проекции точки на прямую необходимо знать координаты точки и параметрическое уравнение прямой. Сначала находим проекцию точки на прямую в направлении, перпендикулярном прямой, а затем смещаем проекцию на расстояние, равное расстоянию от начала координат до прямой.

Где применяются проекции в математике?

Проекции широко применяются в различных областях математики и физики. Они используются в геометрии, статистике, компьютерной графике, инженерии и других дисциплинах. Например, проекции используются при построении трехмерных моделей, решении геодезических задач, построении графиков и т. д.

Могут ли проекции помочь в решении геометрических задач?

Да, использование проекций может значительно упростить решение геометрических задач. Проекции позволяют представить сложные трехмерные объекты в двумерном пространстве и анализировать их свойства. Они также помогают визуализировать и понять геометрические конструкции и взаимное расположение объектов.

Что такое проекция в математике?

В математике проекция – это операция, с помощью которой можно отобразить объект на плоскость или пространство. Проекция позволяет получить изображение объекта, которое сохраняет некоторые его характеристики, например, форму и размеры.

Алгебраическая интерпретация проекции

В математике проекция может быть интерпретирована в алгебраическом смысле. Алгебраическая интерпретация проекции включает в себя определение проекции в терминах алгебры и использование алгебраических методов для анализа и вычисления проекций.

Алгебраический подход к проекции основан на представлении пространственных объектов, таких как точки, линии и фигуры, в виде алгебраических выражений. В этом случае проекция рассматривается как функция, которая сопоставляет каждому объекту его проекцию на плоскость или другое подпространство.

Алгебраическая интерпретация проекции позволяет использовать алгебраические методы для работы с проекциями. Например, можно использовать алгебраические операции, такие как сложение, вычитание и умножение, для комбинирования и преобразования проекций. Также можно применять алгебраические методы для решения задач, связанных с проекциями, например, для нахождения пересечений или расстояний между проекциями.

Алгебраическая интерпретация проекции находит применение во многих областях, таких как геометрия, компьютерная графика, инженерия и физика. Она позволяет упростить и стандартизировать работу с проекциями, а также решать сложные задачи, связанные с преобразованиями и анализом проекций.

Проекция на плоскость

Примеры проекции на плоскость включают проекцию точки на плоскость, проекцию прямой на плоскость, проекцию фигуры на плоскость и т. д. В каждом из этих примеров проекция позволяет увидеть объект или его часть в двухмерном представлении на плоскости.

Проекция на плоскость может быть ортогональной или параллельной. Ортогональная проекция происходит, когда плоскость, на которую проецируется объект, перпендикулярна оси проекции. Параллельная проекция происходит, когда плоскость, на которую проецируется объект, параллельна оси проекции.

Проекция на плоскость имеет много применений. Например, в инженерии она используется для создания чертежей и моделей объектов, а в компьютерной графике – для создания трехмерных изображений на двумерных экранах. Также проекция на плоскость широко используется в географии, архитектуре и других областях, где требуется представление объектов в двухмерном виде.

Проекция в трехмерном пространстве

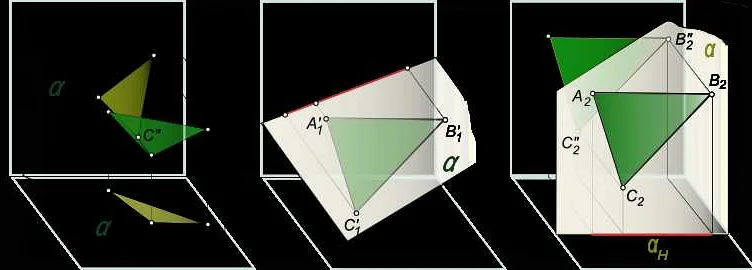
Проекция трехмерного объекта на плоскость получается путем опускания перпендикуляра из каждой точки объекта на плоскость проекции. Таким образом, каждая точка трехмерного объекта преобразуется в точку на плоскости проекции.

Проекция в трехмерном пространстве может быть описана с помощью математической формулы, которая учитывает координаты точек объекта и параметры проекции.

Одним из примеров проекции в трехмерном пространстве является проекция на плоскость XY. В этом случае, координаты точек объекта будут иметь вид (x, y, 0), где х и у — координаты точки на плоскости, а 0 — координата по оси z, которая равна нулю для всех точек проекции на плоскость XY.

ТочкаКоординаты в трехмерном пространствеПроекция на плоскость XY

A	(1, 2, 3)	(1, 2)
B	(-2, 0, 4)	(-2, 0)
C	(3, -1, 5)	(3, -1)

В данном примере, точки A, B и C являются проекциями точек трехмерного объекта на плоскость XY.

Проекции в трехмерном пространстве находят широкое применение в различных областях, таких как архитектура, инженерия, компьютерная графика и дизайн.

Проекция в компьютерной графике

Проекция в компьютерной графике основывается на математическом преобразовании, которое переводит трехмерные координаты объекта в двумерные координаты на экране. В результате проекции объекта на плоскость получается его изображение, которое сохраняет глубину и пропорции оригинала, но теряет третье измерение.

Существует несколько типов проекций в компьютерной графике, самые распространенные из которых – это перспективная и ортографическая проекции. Перспективная проекция позволяет создавать реалистичные изображения с эффектом глубины, в то время как ортографическая проекция используется для создания плоских, без искажений изображений.

Проекции в компьютерной графике широко применяются в различных областях, таких как разработка компьютерных игр, анимация, визуализация архитектурных проектов и многое другое. Благодаря проекциям можно создавать реалистичные и привлекательные визуальные эффекты, которые с успехом используются в современных технологиях.

Применение проекции в разных областях

1. Геометрия.

Проекция широко используется в геометрии для изучения фигур и их свойств. Например, проекция точки на прямую позволяет определить ее положение на этой прямой. Проекция также используется при построении различных геометрических фигур, например, проекция точек на плоскости при построении многогранников.

2. Картография.

В картографии проекция используется для отображения трехмерного мира на плоскость карты. Существует множество различных проекций, каждая из которых имеет свои преимущества и недостатки. Проекция позволяет сохранить форму и размеры объектов на карте, но может искажать их углы и расстояния.

3. Компьютерная графика.

Проекция играет важную роль в компьютерной графике, где используется для отображения трехмерных объектов на двумерный экран. Проекция позволяет определить, какие части объекта должны быть видимы на экране, а какие должны быть скрыты.

4. Механика и инженерия.

В механике и инженерии проекция используется для анализа движения и конструкции различных механизмов. Проекция позволяет определить силы, действующие на объекты, и предсказать их поведение.

5. Физика.

В физике проекция используется для изучения различных явлений и величин. Например, проекция вектора скорости позволяет определить его составляющие в различных направлениях. Проекция также используется для анализа электрических и магнитных полей.

Это лишь некоторые примеры применения проекции в разных областях. В целом, проекция является мощным инструментом анализа и позволяет решать разнообразные задачи в различных научных и технических областях.