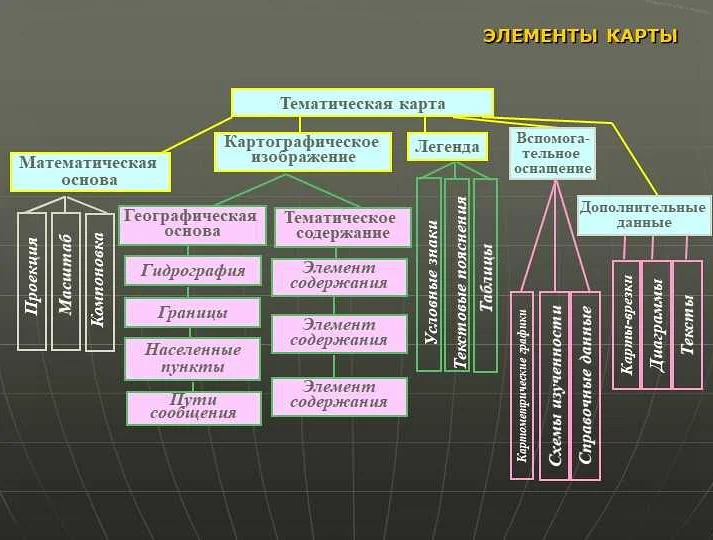
Что входит в математическую основу карты

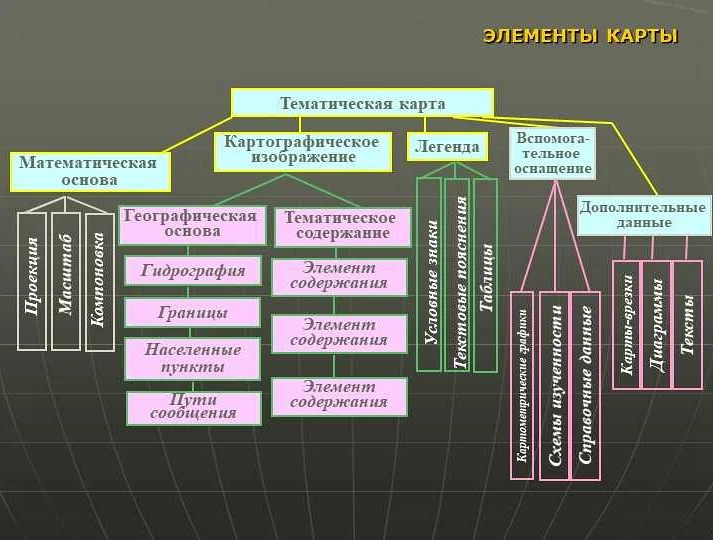
Математическая основа карты включает в себя геометрические принципы, системы координат, проекции и алгоритмы, которые позволяют представить земную поверхность на плоскости. Это позволяет нам создавать и интерпретировать карты, используемые для навигации, изучения географии и анализа пространственных данных.

Карты — это инструмент, который мы используем практически каждый день. Они помогают нам ориентироваться в пространстве, находить места, планировать маршруты и многое другое. Но как именно создаются эти карты? Каким образом мы можем быть уверены в их точности и надежности? Ответ на эти вопросы лежит в основах математики, которые входят в процесс создания карты.

Главным компонентом карты является система координат. Она позволяет определить местоположение объектов на карте и установить связь между реальным миром и его отображением на плоскости. Для этого используется различные математические концепции, такие как геометрия и тригонометрия. Они помогают определить углы, расстояния и направления между объектами на карте.

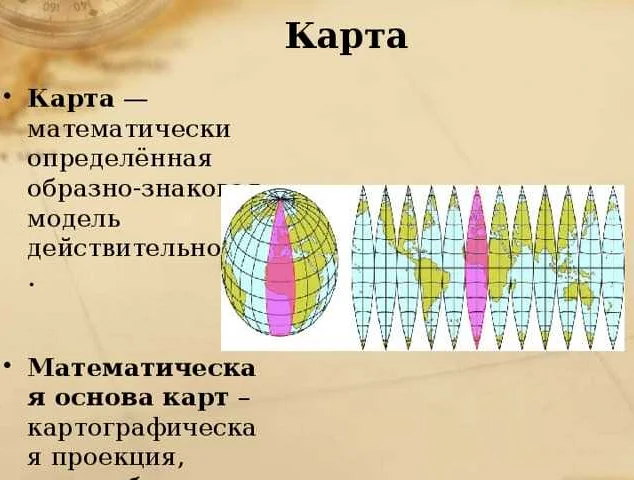
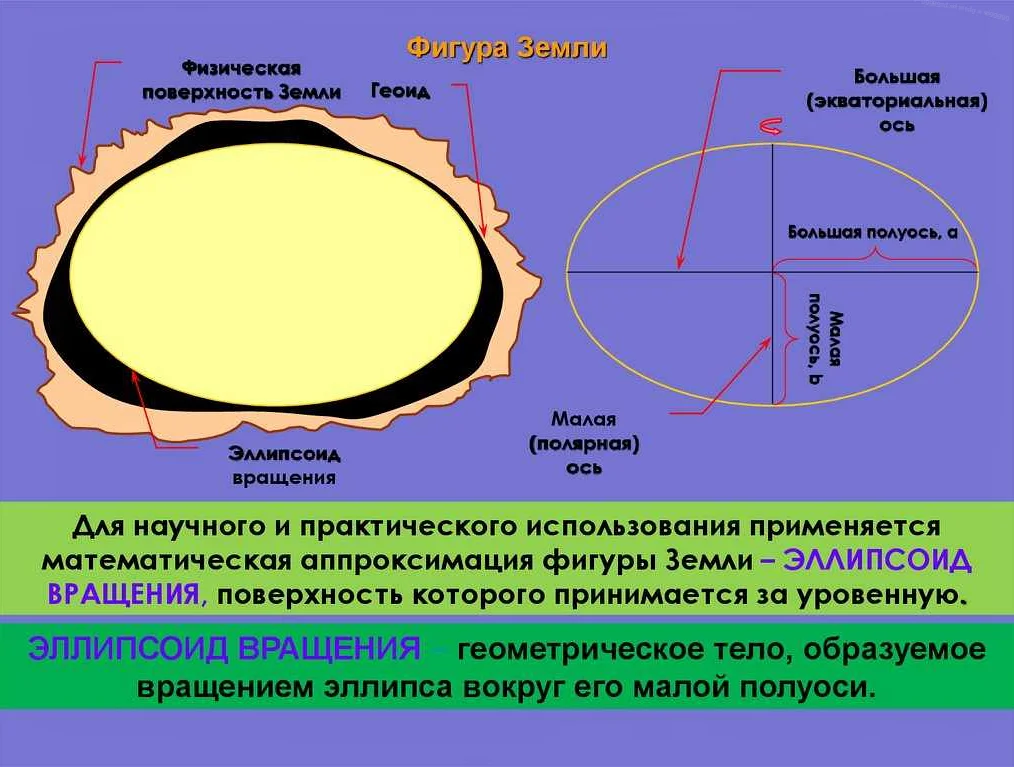
Еще одним важным аспектом создания карты является проекция. Как мы знаем, Земля имеет форму эллипсоида, а не плоскости. Поэтому для отображения поверхности Земли на плоскость используются различные проекции. Эти проекции также основаны на математических принципах и позволяют сохранить определенные свойства карты, такие как сохранение масштаба или сохранение формы объектов.

Таким образом, основы математики играют важную роль в создании карт. Они обеспечивают точность и надежность картографической информации, позволяют нам ориентироваться в пространстве и использовать карты для различных целей. Именно благодаря математике мы можем создавать и использовать карты, которые становятся незаменимым инструментом в нашей повседневной жизни.

Геометрия: основа пространственного представления

Точка — это основной элемент геометрии, который представляет собой местоположение в пространстве. Точки используются для обозначения объектов, таких как города, границы и географические особенности.

Линия — это набор точек, соединенных друг с другом. Линии могут быть прямыми или кривыми и используются для обозначения дорог, рек, границ и других пространственных объектов.

Плоскость — это двумерное пространство, которое может быть использовано для представления поверхности земли или других объектов. Плоскости используются для создания карты и размещения на ней объектов.

Угол — это мера поворота между двумя линиями или плоскостями. Углы используются для определения направления и ориентации объектов на карте, таких как направление дороги или границы.

Геометрия также предоставляет различные методы для измерения и описания пространственных объектов, такие как расстояние, площадь и объем. Эти методы позволяют определить размеры и характеристики объектов на карте.

Таким образом, геометрия является неотъемлемой частью создания карты и предоставляет основу для пространственного представления объектов и их отношений.

Алгебра: расчеты и формулы для картографии

Одной из основных формул, используемых в картографии, является формула масштаба. Масштаб карты обычно выражается в виде отношения длины на карте к длине в реальном мире. Формула масштаба выглядит следующим образом:

масштаб = длина на карте / длина в реальном мире

Также в картографии используется формула для расчета площади поверхности на карте. Формула площади зависит от формы поверхности и может быть различной. Например, для прямоугольной поверхности формула площади будет следующей:

площадь = длина * ширина

Формулы также используются для расчета расстояния между объектами на карте. Например, для расчета расстояния между двумя точками на плоскости можно использовать формулу расстояния между точками:

расстояние = √((x2 — x1)² + (y2 — y1)²)

Все эти расчеты и формулы позволяют создавать точные и информативные карты, которые могут быть использованы для различных целей, таких как навигация, геология, география и даже планирование городской инфраструктуры.

Топология: связность и смежность в картографии

Связность в картографии относится к степени, в которой объекты на карте соединены друг с другом. Это может быть физическая связь, например, дороги или реки, или абстрактная связь, такая как границы административных единиц. Важно понимать связность объектов на карте, чтобы определить доступность и возможные маршруты.

Смежность в картографии относится к тому, как объекты на карте расположены друг относительно друга. Смежные объекты имеют общую границу или соприкасаются. Например, два смежных участка земли имеют общую границу, а два смежных города на карте находятся рядом друг с другом. Понимание смежности помогает определить структуру и связи между объектами на карте.

Важно отметить, что связность и смежность в картографии могут быть представлены и анализированы с использованием топологических моделей и операций. Топологические модели позволяют представить пространственные данные объектов на карте и их отношения друг с другом. Топологические операции позволяют выполнять различные анализы и манипуляции с пространственными данными.

Таким образом, знание топологии, связности и смежности является важным для создания точных и информативных карт. Это позволяет анализировать пространственные данные, определять маршруты и связи между объектами, а также представлять информацию в удобной и понятной форме для пользователей.

Тригонометрия: определение углов и расстояний на карте

Тригонометрия играет важную роль в создании карт, так как позволяет определить углы и расстояния между различными точками на карте. Она базируется на изучении соотношений между сторонами и углами треугольников.

Определение углов на карте основано на принципах геометрии. Угол на карте может быть измерен в градусах, минутах и секундах. Градусы обычно делятся на 60 минут, а минуты на 60 секунд. Таким образом, угол измеряется в градусах, минутах и секундах.

Чтобы определить угол на карте, можно использовать различные методы. Один из них — использование инструментов, таких как теодолит или компас. Также можно использовать тригонометрические функции, такие как синус, косинус и тангенс, для определения угла между двумя линиями или направлениями.

Определение расстояний на карте тоже основано на принципах тригонометрии. Для определения расстояний между точками на карте можно использовать теорему Пифагора или формулы сферической тригонометрии для сферических поверхностей, таких как Земля.

Тригонометрия позволяет определить углы и расстояния на карте с высокой точностью. Это важный инструмент для создания и анализа карт, который используется в различных областях, таких как навигация, геодезия и география.

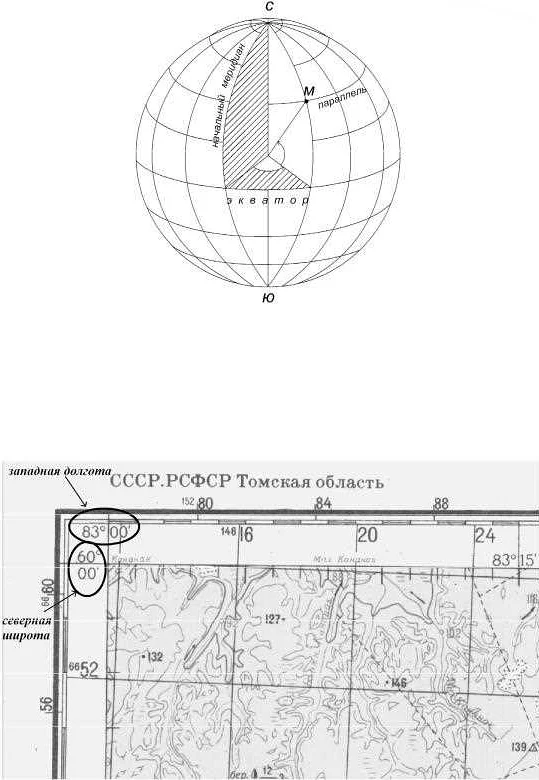
Координатная система: определение точек на карте

На карте координатная система может быть двухмерной или трехмерной. В двухмерной координатной системе точка определяется парой координат — абсциссой (x) и ординатой (y). Абсцисса указывает расстояние точки от вертикальной оси, а ордината — от горизонтальной оси.

В трехмерной координатной системе, используемой в некоторых картах, вводится еще одна координата — высота (z). Точка в трехмерной системе определяется тройкой координат — x, y и z.

Важно отметить, что значения координат могут быть представлены как абсолютными (например, в метрах или градусах), так и относительными (например, в пикселях на экране).

Для удобства работы с координатами на карте, часто используются различные системы проекций. Они позволяют перевести географические координаты (широту и долготу) в плоскую плоскость карты.

Определение точек на карте в координатной системе позволяет создавать различные геоинформационные системы и картографические приложения, а также анализировать пространственные данные.

Проекции: методы преобразования географических данных

Существует множество методов проекций, каждый из которых имеет свои особенности и области применения:

• Цилиндрические проекции: основаны на отображении поверхности Земли на цилиндр. Примеры: меркаторская проекция, равноплощадная проекция.
• Конические проекции: основаны на отображении поверхности Земли на конус. Примеры: ламбертова проекция, альбертса проекция.
• Плоскостные проекции: основаны на отображении поверхности Земли на плоскость. Примеры: азимутальная проекция, ортогональная проекция.

Каждая проекция имеет свои преимущества и недостатки. Некоторые проекции сохраняют форму объектов, но искажают их размеры, другие сохраняют площадь, но искажают форму. Выбор проекции зависит от цели карты и области применения.

Методы преобразования географических данных при использовании проекций также включают в себя определение масштаба, установление системы координат, а также коррекцию искажений. Эти методы позволяют получить точные и удобочитаемые карты, которые широко используются в географии, геологии, навигации и других областях.

Статистика: анализ данных и визуализация на карте

Для анализа данных используются различные методы статистики, такие как среднее значение, медиана, мода, дисперсия и корреляция. Они помогают выявить основные характеристики и связи между различными переменными. Например, с помощью статистического анализа можно определить, насколько средняя зарплата различается по разным регионам на карте.

Визуализация на карте является важным инструментом для объединения статистических данных и пространственной информации. Она позволяет наглядно представить данные на географической карте и выявить географические закономерности. Например, данные о населении можно визуализировать на карте, используя различные оттенки цвета или размеры маркеров для отображения разной плотности населения в разных регионах.

Важно отметить, что визуализация на карте должна быть понятной и информативной. Чтобы эффективно передать данные, можно использовать различные графические элементы, такие как диаграммы, графики, столбцы и линии. Это поможет пользователю быстро и точно проанализировать данные и сделать выводы.

Интерполяция: создание плавных переходов на карте

Когда мы рисуем карту, мы хотим, чтобы переходы между различными элементами были плавными и естественными. Вот где на помощь приходит концепция интерполяции.

Интерполяция — это процесс создания плавных переходов между значениями на карте. Она позволяет нам создавать плавные переходы между цветами, текстурами и другими атрибутами элементов карты.

Для того чтобы использовать интерполяцию, мы должны знать значения атрибутов в различных точках карты. Например, если у нас есть карта с высотой гор, мы можем определить значения высоты в различных точках. Затем мы можем использовать интерполяцию для создания плавных переходов между этими значениями.

Интерполяция может быть использована для создания плавных переходов между любыми значениями на карте, не только высотой гор. Она может быть использована для создания плавных переходов между цветами воды, текстурами земли, интенсивностью освещения и т.д.

Важно отметить, что интерполяция является одним из инструментов, которые мы можем использовать для создания плавных переходов на карте. Она работает в сочетании с другими техниками, такими как сглаживание и блендинг, чтобы создать естественные и привлекательные карты.

Вопрос-ответ:

Какие основы математики лежат в основе создания карты?

Основы математики, лежащие в основе создания карты, включают геометрию, алгебру и топологию. Геометрия используется для определения формы и размеров территории, алгебра — для расчета координат и масштабирования карты, а топология — для отображения связей и отношений между объектами на карте.

Как геометрия используется при создании карты?

Геометрия используется при создании карты для определения формы и размеров территории. На основе геометрических принципов и правил строятся линии, полигоны и точки, которые представляют различные объекты на карте.

Как алгебра применяется при создании карты?

Алгебра применяется при создании карты для расчета координат и масштабирования. С помощью алгебры определяются математические модели и системы координат, которые позволяют точно определить положение объектов на карте и их пространственные отношения. Алгебра также используется для масштабирования карты, чтобы можно было увеличивать или уменьшать ее размер с сохранением пропорций.

Что такое топология и как она применяется при создании карты?

Топология — это раздел математики, который изучает отношения и связи между объектами. В контексте создания карты топология используется для отображения связей и отношений между объектами на карте. Например, топология может помочь определить, какие дороги пересекаются или соприкасаются, какие реки впадают в озера и т.д. Это позволяет создавать более точные и информативные карты.

Каким образом основы математики влияют на точность и качество карты?

Основы математики играют ключевую роль в определении точности и качества карты. Геометрия позволяет определить форму и размеры территории с высокой точностью. Алгебра обеспечивает точное расчет координат и масштабирование карты. Топология позволяет учесть связи и отношения между объектами, что делает карту более информативной. Без использования математики создание карты было бы затруднено, и она была бы менее точной и качественной.

Какие основы математики используются при создании карты?

При создании карты используются различные математические основы. Одна из основных основ — это геометрия. Геометрия позволяет определить форму и размеры объектов на карте, а также рассчитать расстояния между ними. Кроме того, используются алгебраические методы для решения уравнений, связанных с координатами и масштабированием карты. Также используются статистические методы для анализа данных, полученных при создании карты. В целом, математика играет важную роль в создании карты и помогает представить информацию в удобной и понятной форме.

Каким образом математика помогает создать карту?

Математика играет важную роль в создании карты. Она позволяет определить форму и размеры объектов на карте с помощью геометрии. Например, для создания карты города необходимо знать координаты зданий и улиц, а для этого используются алгебраические методы решения уравнений. Кроме того, математика помогает рассчитать расстояния между объектами на карте и провести масштабирование. Например, при создании карты мира необходимо учесть кривизну Земли и провести проекцию, чтобы отобразить ее на плоскости. Все эти математические методы позволяют создать карту, которая будет точной и удобной в использовании.

Видео по теме: