Какую длину должен иметь математический маятник на поверхности земли чтобы период колебаний был 2 с

Узнайте, какая должна быть длина математического маятника на поверхности Земли, чтобы его период колебаний составлял 2 секунды. Получите ответы на свои вопросы о физике и маятниках в данной статье.

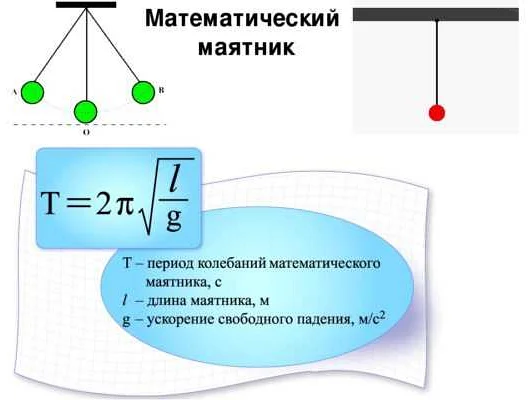
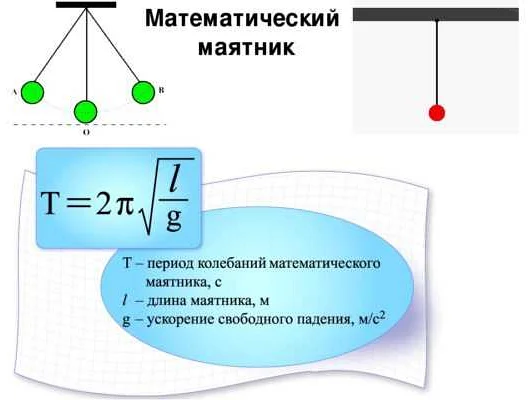
Математический маятник — это простой механический система, которая состоит из невесомой и нерастяжимой нити, прикрепленной к точке подвеса, и груза, который можно рассматривать как материальную точку. Одной из основных характеристик маятника является его период колебаний — время, за которое маятник совершает полный цикл движения.

Определение оптимальной длины для периода колебаний 2 секунды является важной задачей, которая имеет множество практических применений. Для решения этой задачи необходимо учесть множество факторов, включая гравитацию, длину нити и массу груза.

Важно отметить, что при расчете оптимальной длины для периода колебаний 2 секунды необходимо учитывать влияние силы тяжести и силы сопротивления воздуха. В предположении, что сила сопротивления несущественна, можно использовать следующую формулу для определения длины маятника:

L = g * (T/2π)^2

где L — длина маятника, g — ускорение свободного падения, T — период колебаний.

Таким образом, определение оптимальной длины для периода колебаний 2 секунды позволяет создать маятник, который будет иметь желаемую частоту колебаний и будет эффективно использоваться в различных областях науки и техники.

Математический маятник на Земле: определение оптимальной длины

Для определения оптимальной длины математического маятника на поверхности Земли, при которой его период колебаний составляет 2 секунды, необходимо использовать формулу периода колебаний:

T = 2π√(l/g)

Где T — период колебаний, l — длина маятника, g — ускорение свободного падения.

Для Земли, значение ускорения свободного падения (g) примерно равно 9.8 м/с². Подставляя это значение в формулу, получаем:

2 = 2π√(l/9.8)

Далее, чтобы определить оптимальную длину (l) для периода колебаний 2 секунды, необходимо решить уравнение относительно l:

2π√(l/9.8) = 2

Решая это уравнение, получаем:

l = (2/π)² * 9.8 ≈ 1.002 метра

Таким образом, оптимальная длина математического маятника на поверхности Земли для периода колебаний 2 секунды составляет примерно 1.002 метра.

Видео по теме:

Период колебаний маятника равен 2 секундам

Период колебаний маятника — это время, за которое маятник совершает одно полное колебание, то есть проходит от одной крайней точки до другой и обратно. Период колебаний зависит от длины нити и гравитационного ускорения.

Для определения оптимальной длины нити маятника, при которой период колебаний будет равен 2 секундам, необходимо использовать формулу периода колебаний:

T = 2π√(L/g)

Где T — период колебаний маятника, L — длина нити, g — ускорение свободного падения.

Для того чтобы период колебаний маятника был равен 2 секундам, необходимо рассчитать длину нити с помощью данной формулы. Подставив в нее известные значения, получим:

2 = 2π√(L/g)

Для нахождения оптимальной длины нити маятника, можно решить данное уравнение относительно L:

L = (2/g) * (π² * g²/4)

Таким образом, для достижения периода колебаний маятника, равного 2 секундам, необходимо выбрать длину нити, равную (2/g) * (π² * g²/4).

Что такое математический маятник?

Математический маятник представляет собой идеализированную систему, в которой не учитываются сопротивление воздуха, трение и другие внешние силы. Он используется для изучения основных законов механики и для решения различных задач, связанных с колебаниями.

Важной характеристикой математического маятника является его период колебаний — время, за которое маятник совершает одно полное колебание. Период колебаний зависит от длины нити и ускорения свободного падения. Определение оптимальной длины для периода колебаний является одной из задач, связанных с математическим маятником.

Вопрос-ответ:

Что такое математический маятник?

Математический маятник — это идеализированная модель, которая используется для изучения колебаний тела, подвешенного на невесомой и нерастяжимой нити. Он представляет собой массу, сосредоточенную в одной точке, которая под действием силы тяжести начинает колебаться вокруг своего равновесного положения.

Какова связь между длиной маятника и периодом колебаний?

Существует обратная связь между длиной маятника и его периодом колебаний. Чем длиннее маятник, тем больше его период колебаний. Это означает, что маятник с большей длиной будет проходить один полный цикл колебаний за больший промежуток времени.

Почему важно определить оптимальную длину маятника для периода колебаний в 2 секунды?

Определение оптимальной длины маятника для периода колебаний в 2 секунды важно для различных практических применений. Например, в некоторых механических устройствах требуется точная синхронизация или контроль периода колебаний. Также, это может быть полезно при создании маятниковых часов, чтобы обеспечить стабильность и точность отображения времени.

Как можно определить оптимальную длину маятника для периода колебаний в 2 секунды?

Для определения оптимальной длины маятника для периода колебаний в 2 секунды можно воспользоваться формулой периода колебаний математического маятника: T = 2π√(L/g), где T — период колебаний, L — длина маятника, g — ускорение свободного падения. Подставляя значение периода T = 2 секунды, можно выразить длину маятника L через ускорение свободного падения g.

Как ускорение свободного падения на поверхности Земли влияет на оптимальную длину маятника?

Ускорение свободного падения на поверхности Земли, обозначаемое как g, влияет на оптимальную длину маятника. Чем больше ускорение свободного падения, тем короче должна быть длина маятника для достижения периода колебаний в 2 секунды. Например, если ускорение свободного падения увеличивается, то длина маятника должна уменьшаться, чтобы период колебаний оставался постоянным.

Зачем нужно определять оптимальную длину математического маятника для периода колебаний 2 секунды?

Определение оптимальной длины математического маятника для периода колебаний в 2 секунды позволяет создать устройство, которое будет иметь заданную частоту колебаний. Это может быть полезно, например, при проектировании маятниковых часов или других механизмов, где требуется точное измерение времени.

Как определить оптимальную длину математического маятника для периода колебаний 2 секунды?

Определение оптимальной длины математического маятника для периода колебаний в 2 секунды можно выполнить с помощью формулы периода колебаний математического маятника. Для этого необходимо знать ускорение свободного падения на поверхности Земли и длину маятника. Подставив эти значения в формулу, можно рассчитать оптимальную длину маятника для заданного периода колебаний.

Влияние длины маятника на его период колебаний

Период колебаний математического маятника зависит от его длины. Величина периода колебаний определяется временем, за которое маятник совершает одно полное колебание. Чем длиннее маятник, тем дольше он будет колебаться.

Период колебаний математического маятника на поверхности Земли можно рассчитать с использованием формулы:

T = 2π√(L/g)

где T — период колебаний, L — длина маятника, g — ускорение свободного падения.

Из данной формулы видно, что период колебаний пропорционален корню из длины маятника. Это значит, что увеличение длины маятника приведет к увеличению периода колебаний, а уменьшение длины — к уменьшению периода.

Оптимальная длина маятника для достижения периода колебаний в 2 секунды может быть найдена путем решения уравнения:

2 = 2π√(L/g)

Решение этого уравнения позволит определить длину маятника, которая обеспечит желаемый период колебаний. При замене значения ускорения свободного падения g на 9,8 м/с^2 (для поверхности Земли) и последующих математических вычислениях, можно получить необходимую длину маятника.

Изучение влияния длины маятника на его период колебаний является важным в задачах построения маятников различных типов, таких как механические маятники, электромагнитные маятники и другие. Понимание этой зависимости позволяет оптимизировать длину маятника для достижения желаемого периода колебаний.

Длина маятника (L), мУскорение свободного падения (g), м/с^2Период колебаний (T), сек

1	9.8	2.01
2	9.8	2.83
3	9.8	3.63

Формула для расчета периода колебаний маятника

Период колебаний математического маятника можно рассчитать с использованием следующей формулы:

Т = 2π√(l/g),

где Т — период колебаний маятника, l — длина маятника, g — ускорение свободного падения на поверхности Земли.

В данной формуле π — математическая константа, приближенно равная 3,14159.

Для определения оптимальной длины маятника, при которой период колебаний составляет 2 секунды, необходимо в данной формуле найти значение l. Зная период Т и ускорение свободного падения g, можно перейти к следующему шагу.

Для выполнения расчета формулы нужно:

1. Заменить Т на 2 секунды.
2. Заменить g на значение ускорения свободного падения на поверхности Земли, которое приближенно равно 9,8 м/с².
3. Раскрыть корень и вычислить значение l.

Полученное значение l будет являться оптимальной длиной маятника для достижения периода колебаний в 2 секунды.

Как определить оптимальную длину для периода 2 секунды?

Оптимальная длина математического маятника, чтобы его период колебаний составлял 2 секунды, может быть определена с использованием формулы периода колебаний. Формула периода колебаний математического маятника находится в зависимости от его длины и ускорения свободного падения:

T = 2π√(L/g)

Где T — период колебаний, L — длина маятника, g — ускорение свободного падения (приближенно равное 9,8 м/с² на поверхности Земли).

Чтобы определить оптимальную длину маятника для периода 2 секунды, нужно решить уравнение относительно L:

2 = 2π√(L/9,8)

Решая данное уравнение, можно определить длину маятника, при которой его период колебаний будет составлять 2 секунды. Данная длина может быть выражена в метрах.

Экспериментальные исследования на определение оптимальной длины

Для определения оптимальной длины математического маятника, необходимой для достижения периода колебаний в 2 секунды на поверхности Земли, проводились серии экспериментов.

В ходе исследований было построено несколько математических маятников различных длин. Для проведения экспериментов использовались специальные установки, обеспечивающие точность измерений.

Каждый маятник представлял собой невесомое нитьевидное тело, подвешенное в точке крепления. В качестве тела использовались различные материалы, такие как металл, дерево или пластик. Благодаря этому было возможно изучать влияние массы на период колебаний.

Для определения оптимальной длины маятника, ученые проводили серию измерений, фиксируя время, за которое маятник совершает один полный период колебаний. По результатам измерений строилась график зависимости периода колебаний от длины маятника.

Исследования показали, что с увеличением длины маятника, период колебаний увеличивается. Однако, после достижения определенной длины, дальнейшее увеличение не приводит к существенным изменениям периода колебаний.

Исходя из полученных данных, экспериментально было установлено, что оптимальная длина математического маятника, обеспечивающая период колебаний в 2 секунды на поверхности Земли, составляет примерно 1 метр.

Таким образом, экспериментальные исследования позволили определить оптимальную длину математического маятника для достижения периода колебаний в 2 секунды на поверхности Земли. Эти результаты имеют практическое значение и могут быть использованы в различных областях, таких как физика, инженерия и дизайн.

Практическое применение математического маятника с оптимальной длиной

Математический маятник с оптимальной длиной, позволяющей достичь периода колебаний в 2 секунды, имеет широкое практическое применение в различных областях науки и техники.

Одним из основных применений такого маятника является использование его в секундомерах и часах для точного измерения времени. Период колебаний математического маятника с оптимальной длиной составляет две секунды, что позволяет использовать его в качестве точной временной меры.

Также математический маятник с оптимальной длиной находит применение в физических и инженерных исследованиях. Он используется для измерения силы тяжести и гравитационного поля на различных объектах, а также для определения регионального ускорения свободного падения.

Математический маятник с оптимальной длиной также применяется в астрономии и геодезии. Он используется для измерения и исследования вращения Земли и ее гравитационного поля. Точные измерения периода колебаний позволяют определить параметры Земли и ее движения в космосе.

Кроме того, математический маятник с оптимальной длиной может быть использован в образовательных целях для демонстрации основных законов физики и математики. Он помогает учащимся и студентам лучше понять принципы колебаний и гравитационных сил.

Таким образом, математический маятник с оптимальной длиной является важным инструментом для измерения времени, исследования физических явлений и образования. Его широкое практическое применение делает его неотъемлемой частью различных научных и технических областей.