Что такое верная пропорция в математике

Верная пропорция в математике — это отношение, которое сохраняет свою структуру при изменении чисел или величин. Узнайте, как определить верную пропорцию и применить ее в различных математических задачах.

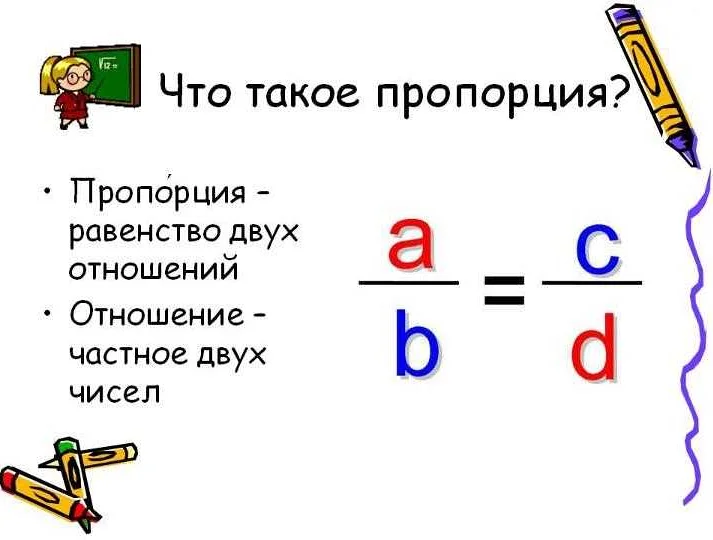
В математике верная пропорция играет важную роль и используется для сравнения двух отношений между несколькими числами или величинами. Пропорция позволяет определить соотношение между различными элементами и является основой для решения множества задач.

Основной принцип верной пропорции заключается в том, что отношение двух чисел должно быть равно отношению двух других чисел. Если дана пропорция a:b = c:d, то можно утверждать, что a и b находятся в таком же отношении, как c и d.

Например, если 3 яблока стоят 15 рублей, то можно сказать, что 6 яблок будут стоить 30 рублей. Здесь отношение цены к количеству яблок остается одинаковым.

Верная пропорция может быть использована для решения различных задач, включая расчеты с процентами, длинами, объемами и другими величинами. Понимание основных принципов верной пропорции позволяет проводить точные вычисления и делать правильные выводы на основе имеющихся данных.

В статье мы рассмотрим основные принципы верной пропорции, а также приведем несколько примеров, чтобы помочь вам лучше разобраться в этой важной математической концепции.

Верная пропорция в математике: основные принципы и примеры

Основной принцип верной пропорции можно выразить следующей формулой:

a/b = c/d

Здесь a и b — первая пара чисел или выражений, а c и d — вторая пара чисел или выражений. Такая формула означает, что отношение между a и b равно отношению между c и d.

Примером верной пропорции может служить задача о распределении яблок между несколькими детьми. Предположим, что имеется 8 яблок и 4 ребенка. Чтобы справедливо распределить яблоки между детьми, можно составить пропорцию:

8/4 = x/1

Здесь x — количество яблок, которое получит каждый ребенок. Решив эту пропорцию, получим:

8/4 = x/1

8 * 1 = 4 * x

8 = 4x

x = 8/4

x = 2

Таким образом, каждый ребенок получит по 2 яблока.

Верная пропорция является важным инструментом в математике и используется для решения различных задач, связанных с отношениями и пропорциями между величинами.

Видео по теме:

Определение верной пропорции

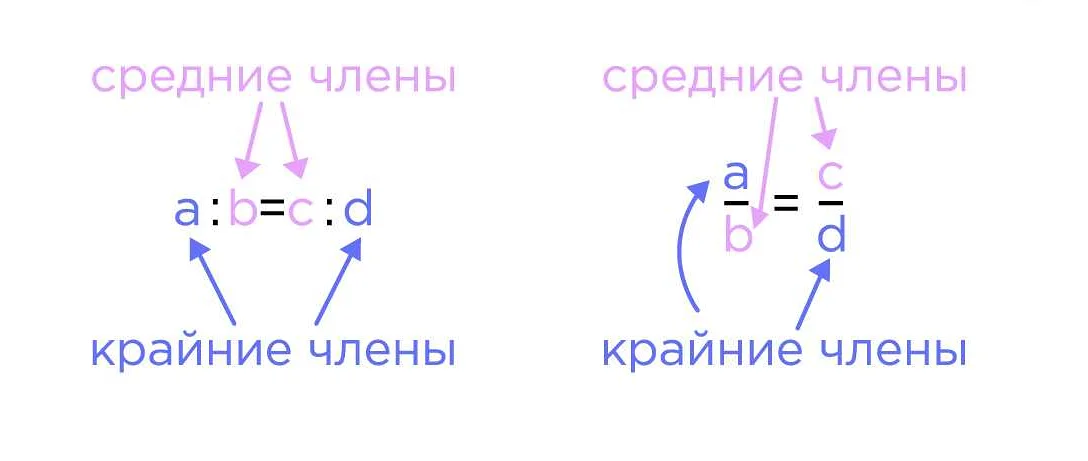
Формально, верная пропорция записывается следующим образом:

a : b = c : d

Здесь a и b представляют одну пару чисел, а c и d — другую. Числа a и c называются первыми членами пропорции, а b и d — вторыми членами.

Верная пропорция можно решать различными способами. Один из них — использование крест-продуктового правила. Согласно этому правилу, произведение первых членов пропорции должно быть равно произведению вторых членов:

a * d = b * c

Также, можно использовать подобные треугольники для решения верной пропорции. Если два треугольника подобны, то соотношение их сторон будет верной пропорцией.

Основные принципы верной пропорции

Основные принципы верной пропорции включают следующее:

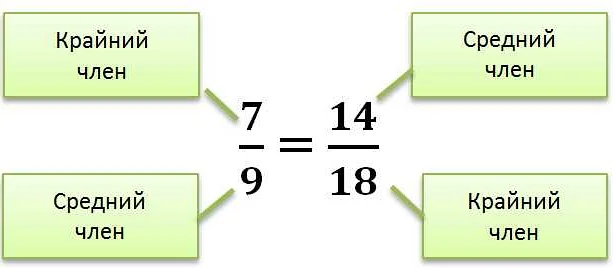
1. Отношение: Верная пропорция определяется через отношение между четырьмя величинами. Отношение обозначается символом «:» или знаком деления «/». Например, а : b или a/b, где a и b — две измеряемые величины.
2. Равенство отношений: Верная пропорция утверждает, что отношение между первыми двумя величинами равно отношению между последними двумя величинами. Формально записывается как a : b = c : d.
3. Умножение и деление: Верную пропорцию можно умножать или делить на любое число, и она останется верной. Если верная пропорция записана как a : b = c : d, то умножение каждой величины на одно и то же число не изменит отношение между ними.
4. Инверсия: Верную пропорцию можно инвертировать, меняя местами числитель и знаменатель в каждом отношении. Инвертированная пропорция также будет верной. Например, если исходная пропорция записана как a : b = c : d, то инвертированная пропорция будет b : a = d : c.

Основные принципы верной пропорции являются основой для решения множества задач и проблем в математике. Они позволяют сравнивать величины и находить неизвестные значения на основе заданных пропорций.

Вопрос-ответ:

Как определить верную пропорцию в математике?

Верная пропорция в математике определяется тем, что отношение между четырьмя числами или величинами остается постоянным.

Какие принципы лежат в основе верной пропорции?

Основные принципы верной пропорции включают равенство долей, свойство перестановки, свойство сокращения и свойство расширения.

Можете привести примеры верной пропорции?

Конечно! Примерами верной пропорции могут быть следующие: 2:3 = 4:6, 5:10 = 1:2 и 3:6 = 2:4.

Как можно использовать верную пропорцию в решении задач?

Верная пропорция может использоваться для решения задач, связанных с пропорциональными отношениями, например, при расчете длины сторон подобных фигур или при нахождении неизвестного значения в пропорции.

Что будет, если пропорция не является верной?

Если пропорция не является верной, то отношение между числами или величинами не будет постоянным, и это будет указывать на нарушение пропорциональных отношений.

Применение верной пропорции в решении задач

Применение верной пропорции особенно полезно в задачах, связанных с пропорциональностью. Например, при решении задач на смешивание веществ, можно использовать пропорцию для определения необходимого количества каждого компонента. Если известно, что для достижения желаемого эффекта нужно смешать вещество A и вещество B в определенном соотношении, то можно составить пропорцию и решить ее, чтобы найти нужные количества компонентов.

Другим примером применения верной пропорции может быть решение задач на доли и проценты. Если известно, что некоторая величина составляет определенную часть от другой величины, можно использовать пропорцию, чтобы найти неизвестную величину. Например, если известно, что 40% суммы равны 200 рублям, то можно составить пропорцию и решить ее, чтобы найти общую сумму.

Применение верной пропорции также может быть полезно при решении задач на скорость и расстояние. Если известно, что одно тело движется с постоянной скоростью, а другое тело движется с переменной скоростью, можно использовать пропорцию для нахождения времени или расстояния. Например, если известно, что одно тело движется со скоростью 60 км/ч в течение 2 часов, а второе тело движется со скоростью 40 км/ч в течение неизвестного времени, можно составить пропорцию и решить ее, чтобы найти время, за которое второе тело пройдет определенное расстояние.

Таким образом, верная пропорция является важным инструментом при решении различных задач в математике. Она позволяет установить соотношение между неизвестными величинами и использовать это соотношение для нахождения нужной величины. Применение верной пропорции особенно полезно в задачах, связанных с пропорциональностью, долями и процентами, а также скоростью и расстоянием.

Примеры верной пропорции

1. Пропорциональное деление отрезка:

Если отрезок разделен на две части, то их длины будут пропорциональны, то есть отношение длин одной части к длине другой будет постоянным. Например, если отрезок AB разделен точкой C таким образом, что AC:CB = 2:3, то мы можем сказать, что отношение длины AC к длине CB всегда будет равно 2:3, независимо от длины отрезка AB.

2. Пропорциональность смежных сторон в подобных фигурах:

В подобных фигурах, стороны имеют пропорциональные длины. Например, если два треугольника подобны, то соответствующие стороны этих треугольников будут пропорциональны. Это можно выразить следующим образом: AB:DE = BC:EF = AC:DF, где AB, BC и AC — стороны первого треугольника, а DE, EF и DF — стороны второго треугольника.

3. Золотое сечение:

Золотое сечение — это особый случай верной пропорции, когда отношение двух отрезков равно золотому сечению примерно 1:1.618. Это отношение имеет множество математических и геометрических свойств и используется в искусстве, архитектуре и дизайне для создания гармоничных композиций и пропорций.

Это лишь некоторые примеры верной пропорции, которые помогут вам лучше понять этот принцип в математике. Верная пропорция играет важную роль во многих математических концепциях и имеет широкий спектр применений.

Пропорции в геометрии

Пропорция в геометрии может быть представлена в виде отношения равенства двух соответствующих отрезков или сторон фигур. Например, если имеется треугольник ABC и прямая, параллельная одной из его сторон, то отношение длин отрезков, образованных пересечением прямой с другими сторонами треугольника, будет представлять пропорцию.

Пропорция в геометрии позволяет определить соотношения между длинами, площадями, объемами и другими характеристиками геометрических фигур. Она широко используется в решении задач, связанных с подобием фигур и пропорциональностью их размеров.

Для наглядного представления пропорций в геометрии можно использовать таблицу, в которой будут указаны соответствующие длины, площади или объемы фигур. Такая таблица позволяет легко определить соотношения между различными значениями и использовать их для решения задач.

ФигураДлинаПлощадьОбъем

Треугольник ABC	AB:BC = CD:DE	Площадь треугольника ABC = (AB * BC) / 2	—
Прямоугольник PQRS	PQ:QR = RS:SP	Площадь прямоугольника PQRS = PQ * QR	—
Цилиндр XYZ	—	—	Объем цилиндра XYZ = П * r^2 * h

Пропорции в геометрии играют важную роль при нахождении неизвестных значений, определении размеров и форм фигур, а также в построении и анализе геометрических моделей.

Использование верной пропорции в финансовых расчетах

Одним из применений верной пропорции в финансовых расчетах является определение коэффициента долгосрочной финансовой устойчивости. Для этого необходимо сравнить сумму долгосрочных обязательств предприятия с его собственным капиталом. Если соотношение долга и собственного капитала находится в определенных пределах, это может свидетельствовать о стабильности и устойчивости финансового положения компании.

Верная пропорция также применяется при расчете доли акционерного капитала в общем капитале предприятия. Это позволяет определить долю владельцев акций в общем капитале компании, что важно при оценке эффективности управления акционерами и принятии решений по поводу выплаты дивидендов.

Применение верной пропорции также может быть полезно при расчете коэффициента рентабельности продаж. Для этого необходимо сравнить прибыль компании с ее выручкой от реализации товаров и услуг. Если соотношение прибыли и выручки находится на определенном уровне, это может свидетельствовать о финансовой устойчивости предприятия и эффективности его деятельности.

Таким образом, использование верной пропорции в финансовых расчетах является важным инструментом для анализа и оценки финансовых показателей предприятия. Это позволяет принимать обоснованные решения, определять уровень стабильности и устойчивости компании, а также оценивать эффективность ее деятельности.

Верная пропорция в природе

Пропорция Золотого сечения можно наблюдать в различных элементах природы. Например, многоцветное цветение растений и их расположение на стеблях, спиральная форма раковины улитки или размещение лепестков в цветке – все эти примеры отражают принцип верной пропорции.

Природа использует верную пропорцию для достижения гармонии и эстетической привлекательности. Это связано с тем, что пропорция Золотого сечения считается универсально приятной для глаза и сознания человека. Поэтому она становится основой для создания привлекательных и сбалансированных форм и структур.

Более того, верная пропорция в природе не только обладает эстетическим значением, но и имеет практическое значение. Например, спиральная форма раковин улиток помогает им эффективно перемещаться и защищаться, а пропорции в форме человеческого тела определяют его функциональность и удобство использования.

Таким образом, верная пропорция в природе является неотъемлемой частью ее организации и красоты. Изучение этой пропорции позволяет лучше понять и восхититься удивительными формами и структурами, которые природа создает.