Что такое циркуль в математике
Содержимое
- 1 Что такое циркуль в математике
- 1.1 Что такое циркуль в математике?
- 1.2 Определение и особенности
- 1.3 Структура и принцип работы
- 1.4 Использование циркуля в математике
- 1.5 Геометрические построения
- 1.6 Построение окружностей и дуг
- 1.7 Изучение геометрических фигур
- 1.8 Примеры использования циркуля
- 1.9 Видео по теме:
- 1.10 Вопрос-ответ:
- 1.11 Построение треугольника
- 1.12 Построение окружности
Циркуль в математике – это инструмент, который используется для построения и измерения окружностей и дуг на плоскости. Он состоит из двух взаимосвязанных ножек, одна из которых фиксирована в центре, а другая может двигаться по масштабной линейке. Циркуль позволяет рисовать окружности заданного радиуса, а также измерять углы и длины дуг. Он является неотъемлемым инструментом для геометрических вычислений и конструирования.
Циркуль — это инструмент, который широко используется в математике для построения окружностей и дуг на плоскости. Он состоит из двух ножек, одна из которых является острием, а другая — карандашом или тонким стержнем. Циркуль позволяет проводить окружности заданного радиуса и строить дуги заданного угла. Он также может использоваться для измерения расстояний, построения перпендикуляров и других геометрических конструкций.
В математике циркуль применяется в различных областях, таких как геометрия, тригонометрия, аналитическая геометрия и многие другие. Он позволяет строить окружности и дуги, изучать их свойства, а также решать различные задачи, связанные с геометрией. Например, циркуль может использоваться для построения окружности, описанной вокруг треугольника, или для нахождения средней линии между двумя точками.
Циркуль также является важным инструментом при решении задач по тригонометрии. С его помощью можно построить окружность с заданным радиусом и центром в начале координат, а затем измерить угол, который описывает точка на этой окружности. Таким образом, циркуль позволяет решить задачи, связанные с определением геометрических характеристик окружностей и дуг.
Примеры использования циркуля можно найти в различных областях математики, таких как геометрия, алгебра и анализ. Например, в геометрии циркуль используется для построения окружности, проходящей через три заданные точки. В алгебре его можно использовать для решения уравнений, связанных с окружностями и дугами. В анализе циркуль может быть полезен для изучения радиуса сходимости степенного ряда или определения границы функции. В целом, циркуль является мощным инструментом, который помогает математикам проводить точные и качественные исследования в различных областях математики.
Что такое циркуль в математике?
Циркуль часто используется в геометрии для проведения окружностей, описывающих треугольники, круги, а также для нахождения точек пересечения окружностей и проведения касательных к ним.
Один из основных принципов работы с циркулем — это регулировка расстояния между ножкой и карандашом. Это позволяет создавать окружности с различными радиусами и строить разнообразные фигуры.
Циркуль — важный инструмент в математике, который помогает ученым и студентам проводить множество геометрических операций и конструировать различные фигуры.
Примеры использования циркуляОписание
| Построение окружности с заданным радиусом | Циркуль позволяет с легкостью построить окружность с заданным радиусом, просто устанавливая ножку в центре и двигая карандаш по окружности. |
| Построение касательной к окружности | С помощью циркуля можно построить касательную линию к окружности, устанавливая ножку в точке на окружности и двигая карандаш вдоль ее. |
| Построение окружности, описывающей треугольник | Циркуль можно использовать для построения окружности, которая описывает треугольник, устанавливая ножку в одной из вершин треугольника и рисуя окружность, которая проходит через две другие вершины. |
Определение и особенности
Основная особенность циркуля заключается в том, что он позволяет строить окружности с заданным радиусом. Для этого необходимо установить нож циркуля на нужную длину и закрепить его. Затем циркулем можно провести окружность, устанавливая нож в нужную точку и вращая его вокруг стержня.
Циркуль широко используется в математике и геометрии для решения различных задач. Он позволяет строить окружности, измерять расстояния и проводить различные конструкции. Также циркуль может использоваться для построения окружностей с заданным радиусом в других областях, например, в архитектуре и инженерии.
Важно отметить, что при использовании циркуля необходимо быть осторожным, чтобы избежать травм или повреждений. Также следует помнить, что циркуль предназначен для работы на плоских поверхностях, и его использование на других материалах может быть затруднительным или невозможным.
Структура и принцип работы
Для работы с циркулем, неподвижная ножка закрепляется на бумаге или другой поверхности, а подвижная ножка используется для рисования окружностей или дуг. Подвижная ножка может быть регулируемой, чтобы изменять радиус окружности.
Принцип работы циркуля основан на использовании математических концепций. Циркуль используется для рисования окружностей с заданным радиусом или дуг с определенным углом. Для этого нужно установить радиус окружности на подвижной ножке и центр окружности на неподвижной ножке. Затем, при помощи ручки на подвижной ножке, вращая циркуль вокруг центра, можно получить окружность или дугу заданного размера.
Циркуль широко используется в геометрии и инженерии для решения различных задач. Он позволяет строить окружности, измерять и сравнивать расстояния, находить центры окружностей и многое другое. Он также используется в художественном творчестве для создания круговых форм и фигур.
Использование циркуля требует точности и аккуратности, чтобы получить точные и симметричные фигуры. Он является незаменимым инструментом для многих математических и геометрических задач, и его применение может быть очень полезным во многих областях.
Использование циркуля в математике
Циркуль широко применяется в математике для решения различных задач и построения геометрических моделей. Вот некоторые примеры использования циркуля:
1. Построение окружности: циркуль используется для рисования окружности с заданным радиусом и центром. Это позволяет построить геометрические фигуры, такие как круги, эллипсы и дуги.
2. Разделение отрезка на равные части: циркуль может быть использован для деления отрезка на равные части. Для этого необходимо установить острие циркуля в одном из концов отрезка и нарисовать дугу, затем повторить эту операцию из другого конца отрезка. Точка пересечения дуг позволит разделить отрезок на равные части.
3. Конструирование углов: циркуль позволяет построить угол заданной величины. Для этого необходимо установить острие циркуля в вершине угла, а затем нарисовать дуги с одинаковым радиусом от каждой стороны угла. Точка пересечения дуг будет определять конечную точку угла.
4. Решение геометрических задач: циркуль может быть использован для решения различных геометрических задач, таких как построение перпендикуляров, биссектрис, треугольников и других фигур.
Использование циркуля в математике позволяет упростить процесс построения геометрических фигур и решения задач, обеспечивая точность и эффективность в работе.
Геометрические построения

Одним из основных инструментов геометрических построений является циркуль. Циркуль позволяет проводить окружности с заданным радиусом и находить точки пересечения окружностей.
С помощью циркуля можно выполнять различные геометрические конструкции, например:
- Построение отрезка: задаются две точки на плоскости, и с помощью циркуля и линейки проводится отрезок, соединяющий эти точки.
- Построение прямой: задаются две точки на плоскости, и с помощью циркуля проводится окружность с центром в одной из точек и радиусом, равным расстоянию между точками. Затем проводится вторая окружность с центром в другой точке и радиусом, равным расстоянию между точками. Прямая проходит через точки пересечения окружностей.
- Построение треугольника: задаются три точки на плоскости, и с помощью циркуля и линейки проводятся отрезки между этими точками. Затем соединяются концы отрезков, образуя треугольник.
Геометрические построения находят широкое применение в различных областях, таких как инженерия, архитектура, дизайн и другие. Они позволяют строить и анализировать геометрические фигуры, решать различные задачи и находить решения в динамике и статике.
Понимание и умение выполнять геометрические построения с использованием циркуля и других инструментов является важным навыком для математиков и инженеров, а также для всех, кто интересуется геометрией и ее приложениями.
Построение окружностей и дуг

Для построения окружности с циркулем, необходимо зафиксировать одну ножку в центре будущей окружности, а другой ножкой провести полный оборот вокруг зафиксированной ножки. При этом острая концовка циркуля оставляет отметки на плоскости, которые образуют окружность.
Дуга – это часть окружности, ограниченная двумя точками на окружности. Для построения дуги с циркулем, необходимо провести полный оборот вокруг точки начала дуги, а затем провести полный оборот вокруг точки конца дуги. Тем самым, острая концовка циркуля оставляет отметки на плоскости, которые образуют дугу.
Циркуль широко применяется в геометрии и инженерии для построения окружностей, дуг, а также для измерения расстояний на плоскости.
Изучение геометрических фигур
Геометрические фигуры — это замкнутые множества точек, которые имеют определенные свойства и характеристики. Изучение геометрических фигур позволяет понять их свойства, классифицировать их и решать задачи, связанные с ними.
Существует множество различных геометрических фигур, таких как круг, прямоугольник, треугольник, квадрат и т.д. Каждая из них имеет свои уникальные характеристики, такие как количество сторон, форма и размеры.
Изучение геометрических фигур помогает развить способность анализировать и решать задачи, а также позволяет улучшить визуальное восприятие и пространственное мышление.
Примеры геометрических фигур:
1. Круг — геометрическая фигура, состоящая из всех точек, которые находятся на одинаковом расстоянии от центра.
2. Прямоугольник — геометрическая фигура с четырьмя прямыми сторонами и углами, равными 90 градусам.
3. Треугольник — геометрическая фигура, состоящая из трех линий, соединяющих три точки.
4. Квадрат — геометрическая фигура с четырьмя равными прямыми сторонами и углами, равными 90 градусам.
Изучение геометрических фигур является важным компонентом математического образования и может применяться в различных областях, таких как архитектура, инженерия, физика и другие.
Примеры использования циркуля
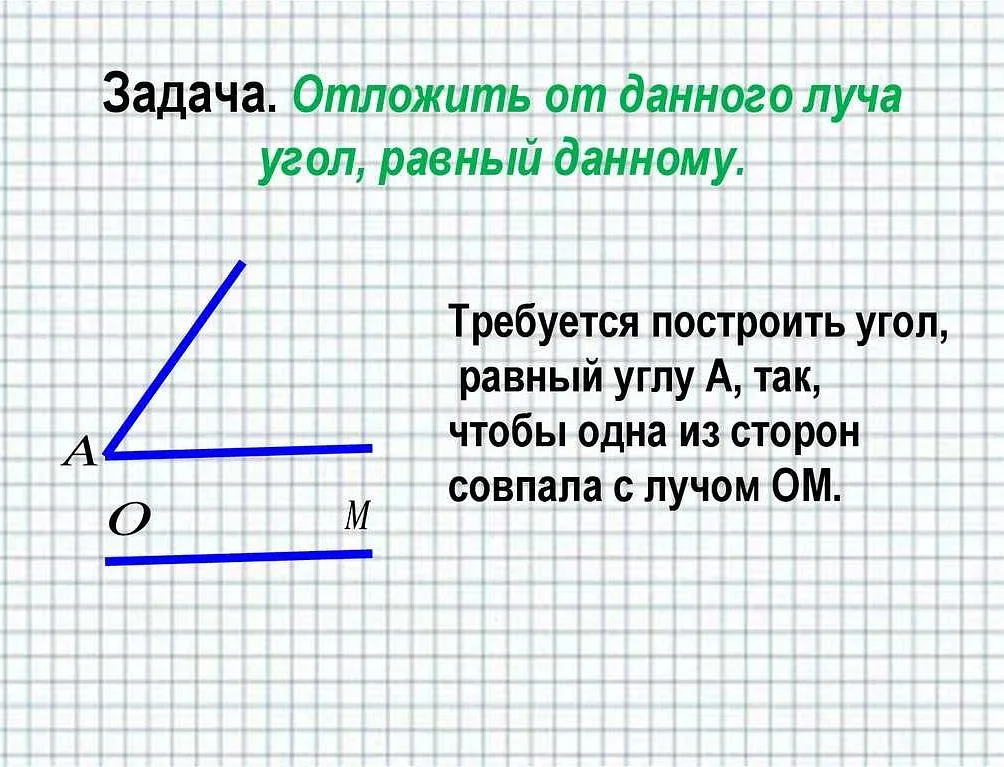
- Построение окружности: циркуль может быть использован для построения окружности с заданным радиусом и центром. Для этого нужно взять циркуль с установленным радиусом и поставить его в центре будущей окружности. Затем, не меняя радиуса, провести окружность вокруг центра, вращая циркуль по 360 градусов.
- Построение дуги: циркуль также может использоваться для построения дуги окружности. Для этого нужно установить нужный радиус на циркуле и определить начальную и конечную точки дуги. Затем, установив циркуль в начальной точке, провести его по дуге до конечной точки, сохраняя одинаковый радиус.
- Построение касательной: циркуль может быть использован для построения касательной к окружности из данной точки на окружности. Для этого нужно установить точку на окружности в качестве центра циркуля и установить радиус таким образом, чтобы он касался данной точки. Затем, проведя окружность вокруг этой точки, можно построить касательную к окружности.
- Решение геометрических задач: циркуль может быть использован для решения различных задач, связанных с геометрией. Например, можно использовать циркуль для построения перпендикуляров, биссектрис, углов и других геометрических фигур.
Это лишь некоторые примеры того, как можно использовать циркуль в математике. Циркуль является важным инструментом для работы с окружностями и геометрическими фигурами.
Видео по теме:
Вопрос-ответ:
Что такое циркуль в математике?
Циркуль — это математический инструмент, который используется для построения окружностей и окружных дуг на плоскости.
Как использовать циркуль в математике?
Для использования циркуля необходимо закрепить его в центре нужной точки на плоскости, затем установить подходящий радиус и кружить им вокруг точки, чтобы получить окружность или дугу.
Где можно применить циркуль в математике?
Циркуль может быть использован в различных областях математики, таких как геометрия, тригонометрия, аналитическая геометрия и т.д. Он может использоваться для построения графиков функций, нахождения точек пересечения, а также для решения геометрических задач.
Какие примеры использования циркуля в математике?
Примеры использования циркуля в математике включают построение окружности с заданным радиусом и центром, нахождение точек пересечения окружностей, построение дуги заданной длины и т.д.
Можно ли использовать циркуль для решения сложных математических задач?
Да, циркуль может использоваться для решения сложных математических задач. В сочетании с другими инструментами и методами, он может быть полезным инструментом для решения геометрических задач, нахождения точек пересечения функций и т.д.
Построение треугольника
Для начала, возьмите циркуль и установите его на одной из вершин треугольника. Затем, используя отрезок, соединяющий эту вершину с другой вершиной, установите циркуль на этом отрезке и отметьте точку на нем. Повторите эту операцию для третьей вершины треугольника.
Если известны длины сторон треугольника, можно использовать циркуль для построения углов треугольника. Начните с установки циркуля на одной из вершин треугольника и отметьте точку на одной из сторон треугольника. Затем, переместите циркуль на другую вершину и отметьте точку на другой стороне треугольника. Повторите эту операцию для третьей вершины треугольника. Затем, соедините полученные точки, чтобы получить углы треугольника.
Построение треугольника с использованием циркуля позволяет точно определить его форму и размеры. Это особенно полезно при решении геометрических задач или при создании точных диаграмм.
Построение окружности
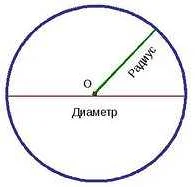
Для построения окружности необходимо знать координаты ее центра и радиус. В математике существует несколько способов построения окружности:
СпособОписание
| С использованием центра и радиуса | Данный способ основан на использовании циркуля и линейки. Сначала на плоскости отмечается центр окружности, затем с помощью циркуля из центра проводится окружность с заданным радиусом. |
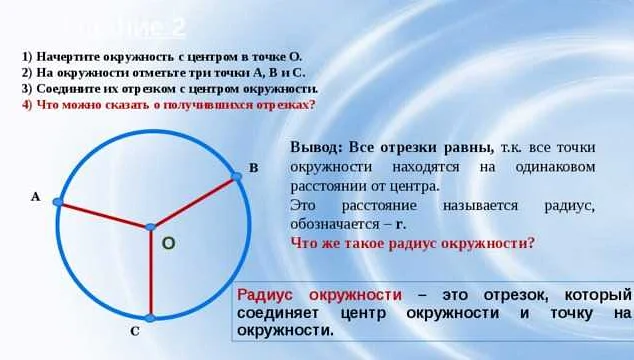
| С использованием трех точек на окружности | Для построения окружности с помощью трех точек на ней необходимо провести перпендикуляры к отрезкам, соединяющим данные точки. Точка пересечения перпендикуляров будет являться центром окружности, а расстояние от центра до любой из трех точек будет равно радиусу окружности. |
| С использованием диаметра | Если известно значение диаметра окружности, то ее центр можно найти путем проведения прямой через две точки, лежащие на окружности и делящие ее на две равные части. |
Важно отметить, что для построения окружности важно следить за точностью измерений и координат, поскольку даже небольшая погрешность может привести к значительным искажениям в геометрической фигуре.

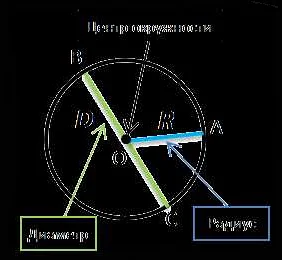
Циркуль — важный инструмент в математике, который помогает строить окружности и измерять расстояния на плоскости. Он используется для решения различных задач, таких как построение перпендикуляров, поиска середин отрезков и нахождения точек пересечения. Циркуль позволяет строить окружности с заданным радиусом, используя его два острия — одно в качестве центра окружности, другое для отметки длины радиуса. Также циркуль может быть использован для измерения расстояний на плоскости. Для этого достаточно приложить одно острие к начальной точке, а другое — к конечной, и затем измерить полученное расстояние на линейке. Пример использования циркуля — построение окружности с центром в точке А и радиусом 5 см. Для этого нужно приложить одно острие циркуля к точке А, а другое — отметить длину радиуса. Затем, не меняя длину радиуса, повернуть циркуль вокруг точки А, получая точки, принадлежащие окружности. Циркуль — незаменимый инструмент для математиков и инженеров, помогающий в решении различных задач. Он позволяет точно и удобно строить геометрические фигуры на плоскости и измерять расстояния.
Статья очень интересная и понятная. Раньше я слышал о циркуле, но не знал, что его можно использовать в математике. Теперь я понял, что это необходимый инструмент для построения окружностей и оценки расстояний на плоскости. Очень полезно знать, как пользоваться циркулем, чтобы проводить точные и аккуратные измерения. Было бы здорово, если бы были приведены примеры использования циркуля в различных математических задачах. Я уверен, что этот инструмент поможет мне в дальнейших изучениях математики и решении сложных задач. Спасибо за информативную статью!