Математика 6 класс тема что такое отношение
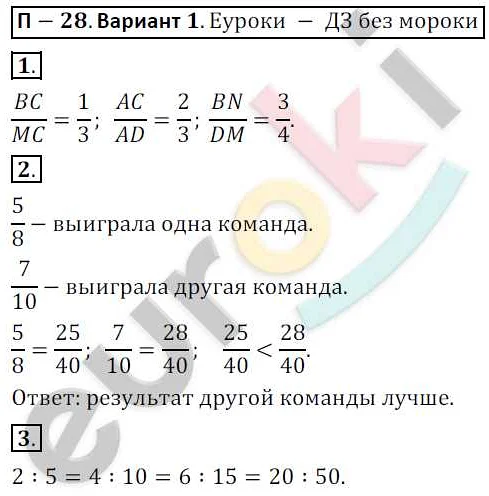
Содержимое
- 1 Математика 6 класс тема что такое отношение
- 1.1 Знакомство с отношением в математике
- 1.2 Определение отношения
- 1.3 Примеры отношений
- 1.4 Как понять отношение?
- 1.5 Свойства отношений
- 1.6 Вопрос-ответ:
- 1.6.0.1 Какое определение можно дать отношению в математике?
- 1.6.0.2 Какими способами можно представить отношение?
- 1.6.0.3 Что такое упорядоченная пара в математике?
- 1.6.0.4 Как можно понять отношение между двумя элементами?
- 1.6.0.5 Какие свойства может иметь отношение?
- 1.6.0.6 Что такое отношение в математике?
- 1.6.0.7 Как понять, что элементы связаны между собой?
- 1.7 Отношения в реальной жизни
- 1.8 Видео по теме:
Отношение в математике 6 класса — это способ связи между элементами двух множеств. В статье рассматривается понятие отношения, его свойства и применение в решении задач. Узнайте, как определить отношение и применить его на практике.
В шестом классе впервые встречается понятие отношения, которое играет важную роль в математике. Отношение — это связь между двумя множествами, которая показывает, какие элементы одного множества соответствуют элементам другого множества. Оно является ключевым понятием для понимания алгебры и геометрии.
Отношения можно представить в виде таблицы или графика. В таблице каждому элементу первого множества соответствует один или несколько элементов второго множества. Например, отношение «быть родителем» может быть представлено таблицей, где каждому ребенку соответствуют его родители.
График отношения показывает связь между элементами двух множеств на координатной плоскости. Каждая точка на графике представляет пару элементов, где первый элемент принадлежит первому множеству, а второй — второму. Например, график отношения «быть друзьями» может показать, кто с кем дружит.
Отношения помогают понять и описать взаимосвязи между элементами различных множеств. Изучение отношений является важным шагом на пути к пониманию более сложных математических концепций, таких как функции и графы. Умение анализировать и интерпретировать отношения поможет ученикам развить логическое мышление и применять математические знания в решении задач.
Знакомство с отношением в математике
Отношение может быть представлено в виде таблицы, называемой таблицей отношений. В таблице отношений каждый элемент представлен в виде строки и столбца, и связи между элементами отображаются в ячейках таблицы.
Элементы множествОтношение
| A | B |
| C | D |
| E | F |
Например, в таблице отношений выше элементы A и B связаны, элементы C и D связаны, и элементы E и F связаны.
Отношение также может быть представлено в виде графа, где каждый элемент представлен вершиной графа, а связи между элементами — ребрами.
Отношение играет важную роль в математике и других областях науки, таких как физика, экономика и информатика. Оно позволяет анализировать и понимать взаимосвязи и зависимости между различными элементами, что помогает нам решать задачи и делать выводы.
Определение отношения
Отношение может быть представлено в виде таблицы, графика или формулы. Например, отношение «больше» может быть представлено в виде таблицы, где каждый элемент первого множества сравнивается с каждым элементом второго множества и указывается, является ли первый элемент больше второго.
Отношение между двумя объектами или множествами может быть различным. Например, отношение может быть симметричным, когда если объект A связан с объектом B, то и объект B связан с объектом A. Отношение может быть также рефлексивным, когда каждый объект связан сам с собой.
Важно понимать, что отношение не обязательно должно быть симметричным или рефлексивным. Отношение может быть любым и зависит от конкретной ситуации или задачи, в которой оно рассматривается.
Примеры отношений
В математике отношение представляет собой связь между двумя множествами, где каждый элемент первого множества имеет определенное соответствие во втором множестве. Рассмотрим несколько примеров отношений:
- Отношение «больше». Если рассматривать множество натуральных чисел, то каждое число имеет определенное соответствие в множестве чисел, которые больше данного числа.
- Отношение «меньше». Аналогично предыдущему примеру, каждое натуральное число имеет соответствие в множестве чисел, которые меньше данного числа.
- Отношение «равно». Каждое число имеет соответствие в множестве чисел, которые равны данному числу.
- Отношение «принадлежит». Если рассматривать множество всех животных, то каждое животное имеет соответствие в множестве животных, которые принадлежат определенному виду.
- Отношение «является частью». Рассмотрим множество всех геометрических фигур. Каждая фигура имеет соответствие в множестве фигур, которые являются частью данной фигуры.
Это лишь несколько примеров отношений, которые можно встретить в математике. Отношения играют важную роль в алгебре, геометрии и других разделах математики, и понимание их сущности помогает более глубоко освоить эти науки.
Как понять отношение?
Чтобы лучше понять отношение, можно рассмотреть примеры из реальной жизни. Например, отношение «старше» можно применить к людям в семье или в классе. Если персона А старше персоны В, то можно установить отношение «старше» между этими двумя людьми.
Отношения могут быть различными: равенство, неравенство, принадлежность, включение и т.д. Чтобы более точно определить отношение, нужно задать определенные условия или критерии сравнения.
Отношения могут быть представлены в виде графиков, диаграмм или математических выражений. В математике отношения широко используются для анализа данных, решения задач и прогнозирования результатов.
Понимание отношений помогает нам лучше анализировать и понимать окружающий мир. Оно также является важным инструментом в науке, экономике и многих других областях знаний.
Свойства отношений
- Рефлексивность: каждый элемент множества A связан с самим собой.
- Симметричность: если элемент a связан с элементом b, то элемент b связан с элементом a.
- Транзитивность: если элемент a связан с элементом b, и элемент b связан с элементом c, то элемент a связан с элементом c.
- Антисимметричность: если элемент a связан с элементом b, и элемент b связан с элементом a, то a=b.
Используя эти свойства, мы можем проводить различные операции с отношениями, их объединять, пересекать и находить обратные отношения.
Вопрос-ответ:
Какое определение можно дать отношению в математике?
Отношение в математике — это связь между двумя или более элементами, которая может быть описана с помощью чисел, символов или слов. Оно показывает, как один объект связан или связан с другим и может быть представлено в виде пары упорядоченных элементов.
Какими способами можно представить отношение?
Отношение можно представить с помощью таблицы, графика, множества упорядоченных пар или с помощью словесного описания. Например, отношение «больше чем» между двумя числами можно представить в виде таблицы или графика, где одно число стоит выше другого.
Что такое упорядоченная пара в математике?
Упорядоченная пара — это пара элементов, где порядок элементов имеет значение. Например, пара (3, 5) отличается от пары (5, 3), так как порядок чисел важен. Упорядоченные пары часто используются для представления отношений между объектами.
Как можно понять отношение между двумя элементами?
Для понимания отношения между двумя элементами можно использовать различные методы. Например, можно посмотреть на их взаимное расположение на числовой оси или в таблице, а также описать отношение словами. Также можно посмотреть на их значения и сравнить их между собой, чтобы определить, какой элемент больше, меньше или равен другому.
Какие свойства может иметь отношение?
Отношение может иметь различные свойства, такие как рефлексивность, симметричность, антисимметричность и транзитивность. Рефлексивность означает, что каждый элемент связан с самим собой. Симметричность означает, что если элемент A связан с элементом B, то элемент B связан с элементом A. Антисимметричность означает, что если элемент A связан с элементом B и элемент B связан с элементом A, то A и B должны быть одинаковыми. Транзитивность означает, что если элемент A связан с элементом B и элемент B связан с элементом C, то элемент A также связан с элементом C.
Что такое отношение в математике?
Отношение в математике — это связь между двумя элементами или наборами элементов. Оно может быть представлено в виде таблицы, графика или формулы. Отношение позволяет определить, какие элементы связаны между собой и как они взаимодействуют.
Как понять, что элементы связаны между собой?
Чтобы понять, что элементы связаны между собой, нужно внимательно рассмотреть их характеристики и сравнить их друг с другом. Например, если речь идет об отношении «больше», то можно сравнить числа и определить, какое число больше или меньше. Если речь идет об отношении «является частью», то можно рассмотреть объекты и определить, какой объект является частью другого.
Отношения в реальной жизни
Одним из примеров отношений в реальной жизни является отношение между учениками и их учителями. Учитель играет роль наставника и передает знания ученикам. Это отношение основано на взаимном доверии и уважении, и способствует успешному обучению и развитию учеников.
Другим примером отношений является отношение между родителями и детьми. Родители заботятся о своих детях, обеспечивают их потребности и помогают им в развитии. Это отношение основано на любви, заботе и поддержке, и способствует формированию здоровых и счастливых семейных связей.
Еще одним примером отношений является отношение между друзьями. Дружба строится на взаимопонимании, поддержке, доверии и взаимной выгоде. Друзья делятся радостями и горестями, проводят время вместе и помогают друг другу в трудных ситуациях.
Кроме того, отношения можно наблюдать и в бизнесе. Отношения между работодателем и сотрудниками, между партнерами и клиентами играют важную роль в успешном функционировании организаций. Они основаны на взаимовыгоде, доверии и профессионализме.
Все эти примеры показывают, что отношения являются неотъемлемой частью нашей жизни. Они помогают нам взаимодействовать с окружающими и создавать гармоничные и продуктивные отношения в разных сферах нашей жизни.


Очень интересная статья! Математика иногда кажется сложной, но благодаря вашим объяснениям, я наконец поняла, что такое отношение. Отношение — это связь между двумя наборами чисел или объектов. Как вы объяснили, отношение можно представить в виде таблицы или графика. Это помогает наглядно увидеть, как связаны числа или объекты друг с другом. Теперь я понимаю, что если одно число увеличивается, то и другое тоже увеличивается в соответствии с этим отношением. А если одно число уменьшается, то и другое тоже уменьшается. Это очень полезное знание, которое поможет мне в решении задач на уроках математики. Спасибо вам за такую понятную и доступную статью! Я уже жду, чтобы узнать больше о математике.