Математика 6 класс как найти нок
Содержимое
- 1 Математика 6 класс как найти нок
- 1.1 Что такое наименьшее общее кратное?
- 1.2 Видео по теме:
- 1.3 Определение НОК
- 1.4 Способы нахождения НОК
- 1.5 Вопрос-ответ:
- 1.6 Разложение чисел на простые множители
- 1.7 Нахождение НОК с помощью разложения на простые множители
- 1.8 Метод деления наименьшего числа на каждый из делителей
- 1.9 Примеры нахождения НОК
- 1.10 Задачи на нахождение НОК
Узнайте, как найти наименьшее общее кратное (НОК) двух или более чисел в математике для учеников 6 класса. Определите методы и алгоритмы, которые помогут вам решить задачу нахождения НОК и примените их к различным примерам. Подробное объяснение и примеры помогут вам лучше понять этот математический концепт.
Наименьшее общее кратное (НОК) — это наименьшее число, которое делится на два или более числа без остатка. В математике НОК часто используется для решения различных задач, особенно в области дробей и десятичных дробей.
Для того чтобы найти НОК двух чисел, необходимо разложить каждое из них на простые множители. Затем выбрать каждый простой множитель с максимальной степенью из обоих чисел и перемножить их. Для трех и более чисел процесс аналогичен, только нужно выбрать максимальную степень каждого простого множителя из всех чисел.
Один из способов найти НОК — использовать таблицу умножения. Начните с наименьшего числа и умножайте его на последующие числа, пока не найдете число, которое делится на все заданные числа без остатка. Это число будет являться НОК.
Например, для чисел 4 и 6: разложим их на простые множители — 4 = 2 * 2, 6 = 2 * 3. Выбираем максимальные степени простых множителей: 2^2 * 3 = 12. Таким образом, НОК для чисел 4 и 6 равен 12.
НОК имеет много применений в математике и может быть полезен при решении задач на соотношение пропорций, расчет времени, скорости и других величин. Поэтому важно уметь находить НОК и использовать его в решении различных задач.
Что такое наименьшее общее кратное?
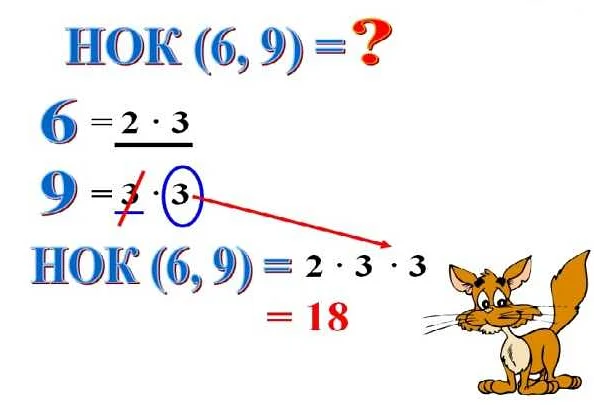
НОК можно найти для двух или более чисел. Для нахождения НОК двух чисел можно использовать несколько методов, однако наиболее распространенным и простым способом является разложение чисел на простые множители.
Разложение числа на простые множители позволяет найти наименьшее общее кратное путем выбора наибольших степеней простых множителей из всех разложений. Например, для чисел 8 и 12, разложение на простые множители будет: 8 = 2^3 и 12 = 2^2 * 3. НОК будет равно 2^3 * 3 = 24.
НОК используется во многих областях математики и естественных наук. Например, НОК может быть использован для определения периодичности волновых функций в физике, для синхронизации процессов в информатике или для решения задач по расписанию и времени в жизни.
Видео по теме:
Определение НОК
Для нахождения НОК двух чисел, нужно найти их общие кратные и выбрать наименьшее из них. Общие кратные чисел можно найти, умножив каждое число на целое число и проверив, делится ли результат на другое число без остатка.
Например, для чисел 4 и 6, общие кратные будут 12, 24, 36 и так далее. Наименьшим общим кратным для этих чисел будет 12.
НОК можно использовать для решения задач, связанных с периодичностью событий, синхронизацией времени и другими задачами, требующими нахождения общего кратного двух или более чисел.
Способы нахождения НОК
Существуют несколько способов нахождения наименьшего общего кратного (НОК) двух или более чисел:
1. Метод разложения на простые множители:
Для нахождения НОК нескольких чисел, каждое число нужно разложить на простые множители. Затем выбираем все простые множители с максимальной степенью из всех разложений и перемножаем их.
2. Метод последовательного деления:
Для двух чисел A и B, начиная с наименьшего числа, последовательно делим его на числа от 2 до максимального из двух чисел. Если полученные остатки равны нулю, то число, на которое делили, является делителем обоих чисел. НОК будет равен произведению всех общих делителей и остаточного числа.
3. Метод таблицы умножения:
Для нахождения НОК двух чисел строится таблица умножения, начиная с наименьшего числа. Затем ищется первое число, которое встречается в обоих столбцах таблицы. Это число и будет НОК.
Зная эти способы, можно легко находить наименьшее общее кратное для различных числовых задач и решать задачи по математике.
Вопрос-ответ:
Что такое наименьшее общее кратное (НОК)?
Наименьшее общее кратное (НОК) двух или более чисел — это наименьшее положительное число, которое одновременно делится на все эти числа.
Как найти НОК двух чисел?
Для того чтобы найти НОК двух чисел, нужно найти их общие кратные, а затем выбрать наименьшее из них. Для этого можно использовать разложение чисел на простые множители.
Как найти НОК трех чисел?
Для того чтобы найти НОК трех чисел, можно последовательно находить НОК первых двух чисел, а затем находить НОК полученного результата и третьего числа. Таким образом, НОК трех чисел будет равен НОК НОК первых двух чисел и третьего числа.
Можно ли найти НОК чисел с помощью таблицы умножения?
Да, можно. Для нахождения НОК двух чисел можно использовать таблицу умножения и искать первое число, которое делится и на одно, и на другое число. Это будет НОК этих чисел.
Как найти НОК большого количества чисел?
Для нахождения НОК большого количества чисел можно использовать метод последовательного нахождения НОК двух чисел. Начните с первых двух чисел и найдите их НОК. Затем найдите НОК полученного результата и третьего числа, и так далее до последнего числа. Полученное значение будет НОК всех данных чисел.
Разложение чисел на простые множители

Для разложения числа на простые множители необходимо последовательно делить его на наименьшие простые числа, начиная с числа 2, пока не получится результат, равный 1.
Приведем пример разложения числа 72 на простые множители:
ДелительРезультат
| 2 | 36 |
| 2 | 18 |
| 2 | 9 |
| 3 | 3 |
Таким образом, разложение числа 72 на простые множители будет выглядеть как 2 * 2 * 2 * 3 * 3 = 72.
Разложение чисел на простые множители является важным шагом при решении многих задач в математике, таких как нахождение наименьшего общего кратного и наибольшего общего делителя.
Нахождение НОК с помощью разложения на простые множители
Нахождение наименьшего общего кратного (НОК) двух или более чисел можно осуществить с помощью разложения этих чисел на простые множители.
Для начала необходимо разложить каждое число на простые множители. Простым множителем называется число, которое делится только на себя и на 1. Например, разложение числа 12 на простые множители будет выглядеть следующим образом: 12 = 2 * 2 * 3.
После разложения всех чисел на простые множители, необходимо выбрать максимальные степени каждого простого множителя. Например, если имеются числа 12 = 2 * 2 * 3 и 18 = 2 * 3 * 3, то максимальные степени простых множителей будут следующими: 2^2 и 3^2.
Далее необходимо перемножить выбранные максимальные степени простых множителей. В нашем примере это будет: 2^2 * 3^2 = 4 * 9 = 36.
Таким образом, НОК чисел 12 и 18 равно 36.
Процесс нахождения НОК с помощью разложения на простые множители позволяет найти наименьшее общее кратное двух или более чисел и является одним из методов решения данной задачи.
Метод деления наименьшего числа на каждый из делителей

Для нахождения наименьшего общего кратного (НОК) двух или более чисел можно использовать метод деления наименьшего числа на каждый из его делителей.
Для начала выбирается наименьшее число из заданных. Затем проверяется, является ли это число кратным всем остальным числам. Если оно делится на каждое из них без остатка, то оно является НОК.
Если наименьшее число не является НОК, то его следует увеличить на самое маленькое из его делителей и повторить проверку. Процесс повторяется до тех пор, пока не будет найдено число, которое делится на все заданные числа без остатка. Это число и будет НОК.
Важно отметить, что при использовании данного метода нужно проверять только делители, которые меньше или равны наименьшему числу. Делители, которые больше наименьшего числа, не могут быть его делителями.
Примеры нахождения НОК
Рассмотрим несколько примеров нахождения НОК:
- Пример 1:
Для нахождения НОК чисел 12 и 18, нужно составить их простые множители:12 = 2 * 2 * 3
18 = 2 * 3 * 3
НОК равен произведению всех простых множителей, каждый взятый в максимальной степени:
НОК(12, 18) = 2 * 2 * 3 * 3 = 36
- Пример 2:
Для нахождения НОК чисел 8, 12 и 16, нужно составить их простые множители:8 = 2 * 2 * 2
12 = 2 * 2 * 3
16 = 2 * 2 * 2 * 2
НОК равен произведению всех простых множителей, каждый взятый в максимальной степени:
НОК(8, 12, 16) = 2 * 2 * 2 * 2 * 3 = 48
- Пример 3:
Для нахождения НОК чисел 9 и 15, нужно составить их простые множители:9 = 3 * 3
15 = 3 * 5
НОК равен произведению всех простых множителей, каждый взятый в максимальной степени:
НОК(9, 15) = 3 * 3 * 5 = 45
Таким образом, нахождение НОК требует разложения чисел на простые множители и выбора наибольших степеней каждого простого множителя.
Задачи на нахождение НОК

Вот некоторые типичные задачи, в которых требуется найти НОК:
- Найдите НОК чисел 12 и 18.
- В саду посадили рядом 3 одинаковых дерева. Первое дерево начало цвести через 9 дней, второе — через 12 дней, а третье — через 15 дней. Через какое количество дней все деревья цветут одновременно?
- В компьютерном классе 3 компьютера полностью загрузились сразу, а остальные через 6, 9 и 12 минут соответственно. Через какое время все компьютеры будут загружены одновременно?
- На складе имеется 3 ящика с карандашами, в каждом ящике по 24 карандаша. Сколько карандашей нужно докупить, чтобы разложить их равными группами по 18 в ящики?
- В корзине лежат яблоки и груши. Если из корзины достать по 8 яблок или по 12 груш, то в ней не останется фруктов. Какое минимальное количество яблок и груш может быть в корзине?
Решение каждой задачи на нахождение НОК требует определенных математических навыков и логического мышления. Важно уметь разбираться в условии задачи и правильно применять методы нахождения НОК.
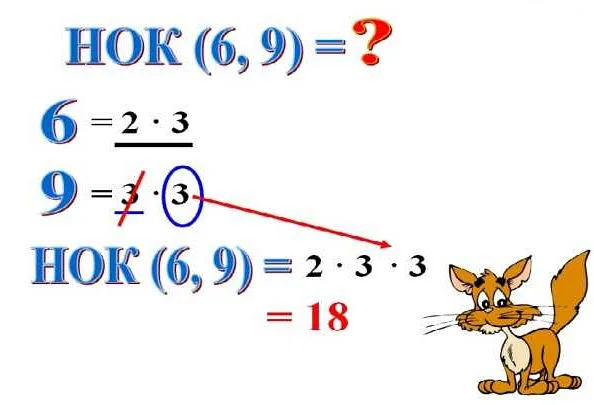


Статья очень полезна и понятна. Она позволяет легко разобраться в теме нахождения наименьшего общего кратного (НОК) в математике. Я узнал, что НОК это наименьшее число, которое делится на все заданные числа без остатка. Автор хорошо объяснил алгоритм поиска НОК. Вся информация представлена логично и последовательно. Я теперь понимаю, что нужно разложить заданные числа на простые множители, а затем взять все эти множители в наивысших степенях и перемножить. Я также оценил примеры, которые помогли мне закрепить новые знания. Статья действительно помогла мне разобраться в этой теме и я готов применить новые знания в практике. Большое спасибо автору за доступное и информативное объяснение.