Методы математического программирования которые требуют наличия системы взаимоувязанных факторов

Методы математического программирования, основанные на использовании системы взаимоувязанных факторов. Узнайте, каким образом эти методы позволяют решать сложные задачи и оптимизировать процессы в различных областях науки, техники и экономики.

Математическое программирование является одной из важнейших областей приложения математики в реальном мире. Оно позволяет находить оптимальные решения в сложных системах с учетом различных ограничений и условий. Однако, часто в реальных ситуациях факторы, влияющие на решение, являются взаимоувязанными и сложно формализуемыми. В таких случаях требуются специальные методы математического программирования, которые учитывают взаимосвязи между факторами.

Одним из таких методов является метод динамического программирования. Он позволяет находить оптимальное решение в задачах с дискретным временем и несколькими связанными событиями. Метод основан на разбиении задачи на подзадачи и последовательном решении каждой из них. Однако, для использования метода динамического программирования необходимо иметь информацию о взаимосвязях между факторами, которая может быть сложно получить в реальных условиях.

Другим методом математического программирования с системой взаимоувязанных факторов является метод анализа иерархий. Он широко применяется в принятии решений при наличии множества вариантов и множества критериев. Метод основан на иерархической структуре принимаемых решений, где каждый фактор является частью более общего фактора. Метод анализа иерархий позволяет учесть взаимосвязи между факторами и определить вес каждого фактора при принятии решения.

В итоге, методы математического программирования с системой взаимоувязанных факторов играют важную роль в решении сложных задач с учетом взаимосвязей между факторами. Они позволяют находить оптимальные решения в условиях неопределенности и ограничений, сокращая время и затраты на принятие решений.

Методы математического программирования

Методы математического программирования представляют собой математические инструменты, используемые для решения сложных задач оптимизации. Они позволяют находить оптимальные решения в различных областях, таких как экономика, инженерия, логистика и другие.

Основной задачей математического программирования является нахождение набора параметров, которые обеспечивают наилучшее значение целевой функции при заданных ограничениях. Целевая функция может быть связана с максимизацией прибыли, минимизацией затрат, оптимальным распределением ресурсов и другими аспектами.

Существуют различные методы математического программирования, в том числе линейное программирование, целочисленное программирование, нелинейное программирование и динамическое программирование. Каждый из этих методов имеет свои особенности и применяется в зависимости от конкретной задачи и ее характеристик.

Линейное программирование является одним из наиболее распространенных методов математического программирования. Оно основано на линейной целевой функции и линейных ограничениях. Целочисленное программирование используется, когда значения переменных должны быть целыми числами, что приводит к более точным решениям, но требует больших вычислительных затрат.

Нелинейное программирование применяется, когда целевая функция или ограничения имеют нелинейную зависимость от переменных. Этот метод требует более сложных вычислительных алгоритмов, но позволяет решать более сложные и реалистичные задачи.

Динамическое программирование используется для решения задач с последовательными решениями, когда решение одного шага влияет на решение следующего шага. Этот метод позволяет находить оптимальное решение, учитывая все возможные варианты развития событий.

Методы математического программирования являются мощными инструментами для решения сложных оптимизационных задач. Они позволяют находить оптимальные решения, учитывая множество взаимосвязанных факторов, и эффективно использовать ресурсы.

Видео по теме:

Система взаимоувязанных факторов

В контексте методов математического программирования важно понимать, что задачу оптимизации часто сложно решить, учитывая только один фактор. Вместо этого, необходимо рассматривать систему взаимоувязанных факторов, которая влияет на решение задачи.

Система взаимоувязанных факторов состоит из нескольких переменных, которые влияют друг на друга и в совокупности определяют оптимальное решение задачи. Важно учесть, что изменение одного фактора может привести к изменению других факторов и, следовательно, к изменению оптимального решения.

Для анализа системы взаимоувязанных факторов часто используются методы математического моделирования, такие как линейное программирование, динамическое программирование и нелинейное программирование. Эти методы позволяют учесть взаимосвязь между переменными и найти оптимальное решение задачи.

Например, при решении задачи оптимизации производства необходимо учесть такие факторы, как стоимость сырья, объем производства, спрос на продукцию, затраты на транспортировку и другие. Изменение любого из этих факторов может повлиять на остальные и на итоговое решение.

Таким образом, для успешного решения задачи оптимизации необходимо учитывать систему взаимоувязанных факторов и использовать методы математического программирования, которые позволяют анализировать и оптимизировать сложные системы.

Принципы математического моделирования

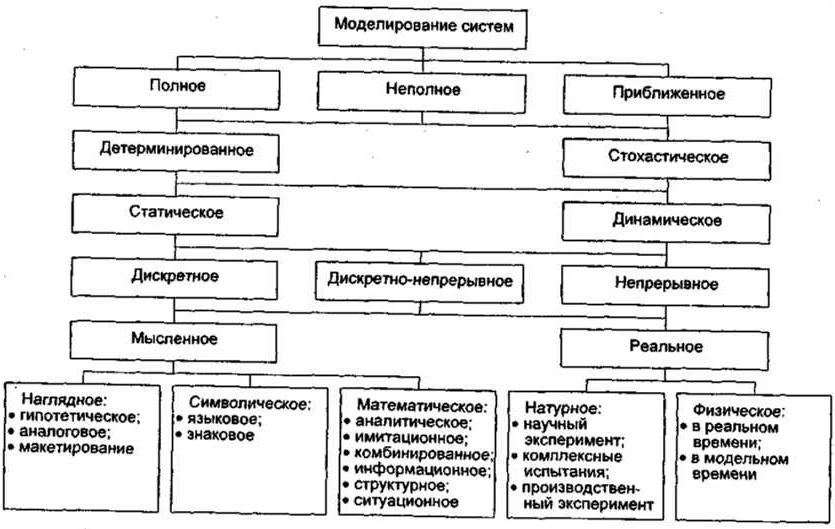
В процессе математического моделирования следуют определенные принципы, которые помогают создать качественную и эффективную модель:

1. Упрощение и абстрагирование	Модель должна быть упрощенной версией реальной системы. Необходимо выделить основные характеристики и связи, игнорируя незначительные детали. Абстрагирование помогает сфокусироваться на существенных аспектах модели.
2. Формализация	Модель должна быть формализованной, то есть описанной с помощью явных математических выражений и уравнений. Формализация позволяет проводить точные аналитические и численные расчеты.
3. Верификация и валидация	Модель должна быть верифицированной (проверенной на соответствие математическому описанию) и валидированной (проверенной на соответствие реальной системе). Это позволяет убедиться в правильности и достоверности модели.
4. Гибкость и масштабируемость	Модель должна быть гибкой и масштабируемой, чтобы можно было вносить изменения и адаптировать ее под различные условия и ситуации. Гибкость позволяет модели адекватно отражать изменения в реальной системе.
5. Проверка и анализ результатов	Модель должна быть проверена и анализирована на предмет соответствия поставленным целям и получения нужной информации. Анализ результатов позволяет сделать выводы и принять решения на основе моделирования.

Соблюдение этих принципов позволяет создать точную и полезную математическую модель, которая может быть использована в различных областях, таких как экономика, физика, биология и т.д. Математическое моделирование является мощным инструментом для исследования и оптимизации сложных систем.

Оптимизационные методы

Существует множество различных оптимизационных методов, каждый из которых имеет свои преимущества и ограничения. Некоторые из наиболее распространенных оптимизационных методов включают методы линейного программирования, методы целочисленного программирования, методы динамического программирования, методы градиентного спуска и методы мультикритериальной оптимизации.

Методы линейного программирования основаны на линейной модели и позволяют решать задачи оптимизации с линейными ограничениями. Эти методы особенно полезны в экономических и финансовых задачах, где требуется принять решение с учетом ограничений ресурсов.

Методы целочисленного программирования нацелены на решение задач оптимизации, где переменные должны принимать только целочисленные значения. Эти методы находят применение, например, в задачах планирования производства и распределении ресурсов.

Методы динамического программирования основаны на разбиении задачи на подзадачи и нахождении оптимального решения для каждой подзадачи. Это позволяет решать сложные задачи оптимизации, включая задачи с нелинейными ограничениями и дискретными переменными.

Методы градиентного спуска используются для оптимизации функций с помощью итеративного приближения. Они особенно эффективны в задачах оптимизации без ограничений, где требуется найти минимум или максимум функции.

Методы мультикритериальной оптимизации позволяют решать задачи оптимизации с несколькими целевыми функциями. Они помогают найти компромиссное решение, учитывая различные критерии и ограничения.

Выбор оптимизационного метода зависит от характеристик задачи и требуемой точности решения. При выборе метода необходимо учитывать сложность задачи, наличие ограничений и доступные ресурсы. Комбинация различных оптимизационных методов может дать наилучший результат в решении сложных задач оптимизации.

Линейное программирование

Задачи линейного программирования могут быть сформулированы как максимизация или минимизация линейной функции от нескольких переменных при определенных ограничениях. Целевая функция определяет цель оптимизации, а ограничения устанавливают границы, которые должны быть соблюдены.

Для решения задачи линейного программирования используются алгоритмы, которые находят оптимальное решение в виде значения переменных, которое достигает минимума или максимума целевой функции при соблюдении всех ограничений.

Линейное программирование широко применяется в различных областях, таких как экономика, финансы, логистика, производство и др. Оно позволяет решать сложные задачи оптимизации, оптимально распределять ресурсы и принимать обоснованные решения.

Основные преимущества линейного программирования включают возможность моделирования сложных систем, учет взаимосвязей между факторами, эффективность и точность решения задачи оптимизации.

Однако, линейное программирование имеет свои ограничения, такие как предположение о линейной зависимости между переменными, непрерывности и ограниченности решений, а также чувствительность к изменениям входных данных.

В целом, линейное программирование является мощным инструментом для решения задач оптимизации, который позволяет находить оптимальные решения и принимать обоснованные решения в различных областях деятельности.

Нелинейное программирование

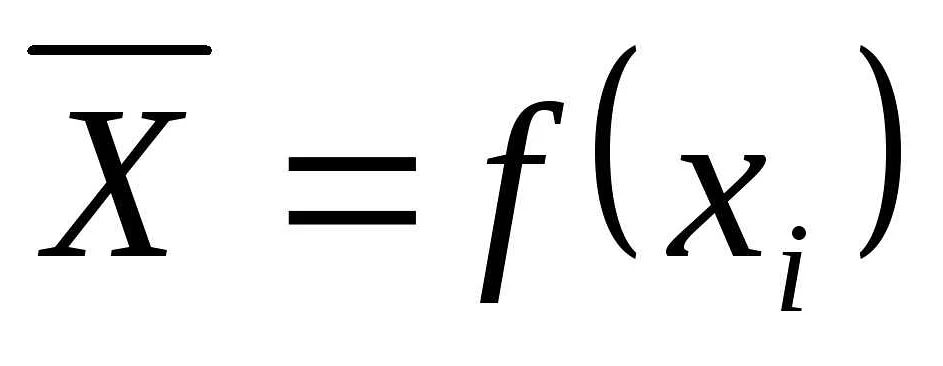
Основная задача нелинейного программирования состоит в нахождении такого набора переменных, при котором достигается минимум или максимум целевой функции. Для этого применяются различные методы, такие как методы градиентного спуска, методы Ньютона-Рафсона и методы последовательного квадратичного программирования.

Нелинейное программирование имеет широкий спектр применений в различных областях, включая экономику, физику, инженерию и биологию. Оно позволяет моделировать сложные системы с учетом взаимоувязанных факторов и находить оптимальные решения для них.

Однако, нелинейное программирование также имеет свои ограничения и сложности. Нелинейные задачи оптимизации могут иметь множество локальных минимумов и максимумов, что затрудняет поиск глобального оптимума. Кроме того, численные методы, применяемые в нелинейном программировании, могут быть вычислительно затратными и требовать больших вычислительных ресурсов.

Динамическое программирование

Основная идея динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз и сохранить полученные результаты для дальнейшего использования. Таким образом, мы избегаем повторного вычисления одних и тех же значений и значительно ускоряем процесс решения задачи.

Один из самых известных примеров применения динамического программирования — задача о рюкзаке. В этой задаче необходимо выбрать некоторый набор предметов, чтобы их общая стоимость была максимальной, но при этом сумма их весов не превышала заданной вместимости рюкзака. Динамическое программирование позволяет решить эту задачу эффективно, разбив ее на множество подзадач.

Динамическое программирование также часто используется для решения задач оптимизации на графах, например, задачи о кратчайшем пути или задачи о расписании. Благодаря разбиению сложной задачи на подзадачи и использованию уже решенных подзадач, мы можем эффективно находить оптимальные решения для этих задач.

В заключение, динамическое программирование является мощным инструментом математического программирования, который позволяет решать сложные оптимизационные задачи с системой взаимоувязанных факторов. Он позволяет эффективно разбивать сложные задачи на более простые подзадачи и использовать уже найденные решения для ускорения процесса решения задачи.

Методы целочисленного программирования

Основная идея методов целочисленного программирования заключается в том, что решение задачи оптимизации представляется в виде набора целочисленных значений переменных, и ищется оптимальное решение среди всех возможных комбинаций целочисленных значений.

Одним из наиболее распространенных методов целочисленного программирования является метод ветвей и границ (Branch and Bound). Этот метод основан на идее разбиения пространства поиска на подпространства и последовательном переборе всех возможных комбинаций значений переменных.

Другим методом целочисленного программирования является метод динамического программирования (Dynamic Programming). В этом методе решение задачи строится на основе рекурсивного подхода и нахождения оптимального значения для каждого подзадания.

Также стоит отметить методы генетических алгоритмов и методы линейного программирования с целочисленными ограничениями.

Методы целочисленного программирования широко применяются в различных областях, включая логистику, производство, транспорт, финансы и другие. Они позволяют решать задачи оптимизации с учетом реальных ограничений и достигать оптимальных решений в условиях, когда требуется использовать только целочисленные значения переменных.

Математическое программирование в реальных задачах

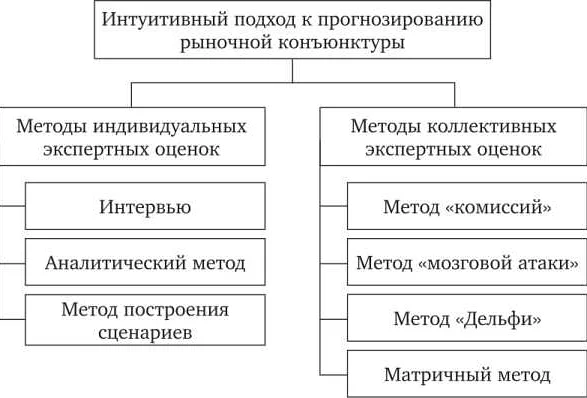
Одной из областей, где математическое программирование широко применяется, является производственная деятельность. С помощью методов математического программирования можно оптимизировать процессы производства, выбрать оптимальное расположение оборудования и максимизировать выход продукции.

Еще одной областью применения математического программирования является логистика. С помощью этого метода можно оптимизировать маршруты доставки грузов, планировать загрузку транспортных средств и управлять запасами на складе.

Также математическое программирование используется в финансовой аналитике и управлении рисками. С помощью математических моделей можно проводить анализ финансовых данных, оптимизировать инвестиционные портфели и прогнозировать риски.

В медицине и биологии математическое программирование применяется для моделирования биологических процессов, оптимизации дозировки лекарств и планирования экспериментов.

Благодаря развитию вычислительной техники и появлению новых методов математического программирования, эта область находится в постоянном развитии. Она помогает нам более эффективно решать сложные задачи и улучшать нашу жизнь.

Вопрос-ответ:

Какие методы математического программирования используются с системой взаимоувязанных факторов?

Система взаимоувязанных факторов может быть решена с использованием различных методов математического программирования, таких как линейное программирование, целочисленное программирование, динамическое программирование и многие другие. Выбор метода зависит от особенностей конкретной задачи и требований.

Какие преимущества имеет использование методов математического программирования для решения системы взаимоувязанных факторов?

Использование методов математического программирования позволяет эффективно оптимизировать систему взаимоувязанных факторов. Это позволяет достичь наилучшего результата с учетом всех ограничений и целей системы.

Каким образом методы математического программирования учитывают взаимоувязанность факторов в системе?

Методы математического программирования учитывают взаимоувязанность факторов в системе путем включения соответствующих ограничений и связей в математическую модель. Это позволяет учесть зависимости между факторами и найти оптимальное решение, учитывающее эти взаимосвязи.

Какие сложности могут возникнуть при использовании методов математического программирования для решения системы взаимоувязанных факторов?

При использовании методов математического программирования для решения системы взаимоувязанных факторов могут возникнуть сложности, связанные с большим объемом данных, сложностью определения связей между факторами и выбором оптимального метода. Также возможны проблемы с вычислительной сложностью и необходимостью учета различных ограничений.

Какие сферы применения имеют методы математического программирования с системой взаимоувязанных факторов?

Методы математического программирования с системой взаимоувязанных факторов могут применяться в различных сферах, таких как экономика, производство, логистика, транспорт, финансы и другие. Они помогают оптимизировать процессы, принимать взвешенные решения и достигать поставленных целей.

Какие методы математического программирования существуют?

Существует несколько методов математического программирования, таких как линейное программирование, целочисленное программирование, динамическое программирование и некоторые другие.

Что такое система взаимоувязанных факторов?

Система взаимоувязанных факторов — это система, в которой каждый фактор оказывает влияние на другие факторы и зависит от них. Взаимоувязанные факторы образуют сложную структуру и взаимодействуют друг с другом, что делает анализ и оптимизацию таких систем сложными задачами.