Методы математической статистики: обзор основных подходов и применений

Статья рассказывает о разных методах математической статистики, которые используются для анализа данных, прогнозирования, выявления зависимостей и многого другого. Ознакомьтесь с наиболее распространенными методами, такими как тестирование гипотез, критерии Стьюдента и Анализ дисперсии (ANOVA), и узнайте, как они могут быть применены в реальной жизни.

Математическая статистика — это раздел математики, который изучает методы получения, анализа и интерпретации данных. Эти методы могут использоваться в различных областях, включая экономику, социологию, физику, медицину и другие. Математическая статистика позволяет сделать выводы о популяции на основе выборочных данных.

Полный обзор методов математической статистики может быть полезен как для начинающих, так и для опытных исследователей. Он включает в себя вероятностные распределения, оценки параметров, проверку гипотез, регрессионный анализ и многое другое. Эти методы могут позволить исследователю делать выводы, основанные на статистических данных, что помогает исследованиям становиться более точными и обоснованными.

В этой статье мы разберем основные методы математической статистики и приведем примеры их применения. Наша цель — помочь вам понять, какие методы использовать для вашего исследования и как интерпретировать результаты.

Что такое математическая статистика?

Математическая статистика — это раздел математики, который изучает методы сбора, анализа и интерпретации данных. Этот дисциплина позволяет ученым делать выводы на основе данных, которые могут быть использованы для принятия решений в различных областях, включая экономику, медицину, социологию и т.д.

Математическая статистика используется для обработки данных, измерения точности и оценки рисков.

Основные задачи математической статистики:

• Сбор данных;
• Анализ данных;
• Проверка гипотез;
• Оценка параметров распределения вероятности;
• Построение статистических моделей;
• Прогнозирование будущих событий;
• Использование статистических методов для принятия решений в бизнесе и науке.

В математической статистике существует ряд методов и техник анализа данных, которые позволяют ученым получать результаты с высокой точностью и надежностью. Некоторые из этих методов включают в себя дисперсионный анализ, корреляционный анализ, регрессионный анализ, как классический, так и бутстрепный, дискриминантный анализ, факторный анализ и др.

Тип тестированияОписание

Одновыборочный t-тест	Сравнивает среднее значение выборки с гипотетическим средним значением популяции.
Двухвыборочный t-тест	Сравнивает средние значения двух выборок, чтобы определить, есть ли статистически значимая разница между ними.
ANOVA	Анализ дисперсии позволяет сравнивать среднее значение более, чем двух групп, для того, чтобы определить, есть ли статистически значимые различия между ними.

Математическая статистика является фундаментальной дисциплиной в науке об обработке и анализе данных. Она позволяет ученым извлекать информацию из данных, делать прогнозы на основе прошлых результатов и принимать обоснованные решения на основе статистических фактов.

Основные понятия в математической статистике

Математическая статистика – это раздел математики, который изучает методы сбора, анализа, интерпретации и оценки статистических данных. Она используется в различных областях, таких как экономика, медицина, физика, социология и др.

Основными понятиями в математической статистике являются:

1. Выборка – это набор данных, полученных из генеральной совокупности.
2. Генеральная совокупность – это общее множество объектов, которые мы исследуем.
3. Статистика – это численная характеристика выборки, например, среднее значение.
4. Параметр – это численная характеристика генеральной совокупности, которую мы хотим оценить.
5. Гипотеза – это предположение о параметрах генеральной совокупности.
6. Уровень значимости – это вероятность того, что мы отвергнем верную гипотезу.
7. Критическая область – это область значений статистики, в которой мы отвергаем гипотезу.
8. Р-значение – это вероятность получить такие или более экстремальные результаты, чем те, которые мы наблюдаем, при условии, что нулевая гипотеза верна.

Понимание и использование этих понятий помогает исследователям и профессионалам в различных областях принимать взвешенные решения на основе статистических данных и придавать этим данным надежность и обоснованность.

Типы данных в математической статистике

Данные в математической статистике бывают разных типов: категориальные, количественные и порядковые. Категориальные данные, также известные как номинальные, представляются не числами, а словами или буквами, обозначающими различные категории, например, цвета или типы продуктов.

Количественные данные, в свою очередь, имеют числовое значение и могут быть представлены дискретными или непрерывными переменными. Дискретные переменные имеют конечное или счетное количество значений и могут быть, например, числом клиентов или числом продаж товара. Непрерывные переменные могут принимать любое значение в заданном диапазоне, например, возраст клиентов или выручка продажи товара.

Порядковые данные предполагают наличие взаимной упорядоченности значений, но не обязательно представлены числами. Например, оценки продуктов доставки, где каждый товар может иметь оценку от 1 до 5, но эти оценки не являются числами, а представлены словами «плохо», «удовлетворительно», «хорошо» и т.д.

Корректное определение типа данных помогает выбрать правильные методы исследований, используемые в математической статистике. Например, для категориальных данных используются методы дискретного анализа, такие как критерий хи-квадрат, а для количественных данных могут использоваться методы графического анализа, например, гистограммы и диаграммы рассеяния.

Методы описательной статистики

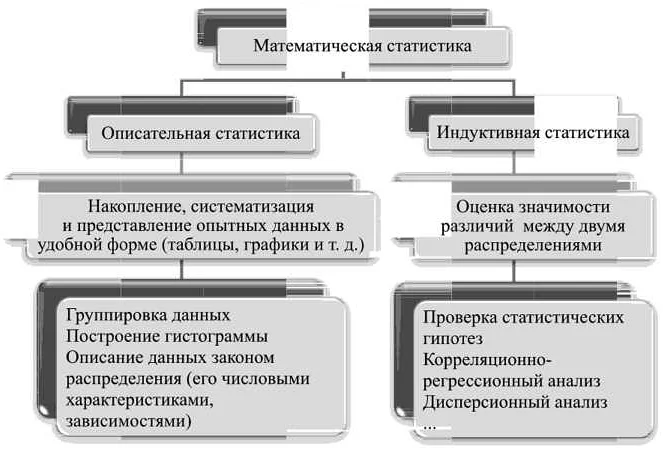
Методы описательной статистики используются для описания количественных данных путем вычисления различных статистических параметров и их визуализации. Они позволяют получить представление о характеристиках набора данных, таких как среднее значение, медиана, мода, дисперсия, стандартное отклонение и интерквартильный размах.

Одним из основных методов описательной статистики является частотный анализ. Он позволяет подсчитать количество различных значений в наборе данных и отобразить их в виде графика частотности.

Другим важным методом является группировка данных. Он позволяет разбить набор данных на категории и оценить количество значений в каждой категории. Этот метод особенно полезен при работе с большими объемами данных.

Еще одним методом описательной статистики является корреляционный анализ. Он позволяет оценить степень взаимосвязи между двумя переменными. Например, можно определить, насколько сильно уровень образования коррелирует с заработной платой в определенной группе людей.

Описательная статистика является важным инструментом для исследования и понимания данных. Она облегчает процесс анализа и позволяет выявлять закономерности и тенденции в данных, делая их более информативными и полезными.

Вероятностные распределения в математической статистике

В математической статистике вероятностные распределения используются для описания случайной величины и ее свойств. Все вероятностные распределения характеризуются параметрами, которые влияют на форму и характер распределения. Некоторые из самых распространенных вероятностных распределений, используемых в математической статистике, приведены ниже.

• Нормальное распределение — самое широко используемое распределение, форма которого напоминает колокол. Оно характеризуется двумя параметрами: средним и стандартным отклонением.
• Биномиальное распределение — используется для описания случаев, когда есть два возможных исхода, например успех или неудача. Оно характеризуется двумя параметрами: числом испытаний и вероятностью успеха.
• Экспоненциальное распределение — используется для описания времени между двумя последовательными событиями. Оно характеризуется одним параметром: средним временем между событиями.
• Равномерное распределение — используется для описания случайных величин с равным шансом на выбор каждого значения. Оно характеризуется двумя параметрами: минимальным и максимальным значениями.

Выбор правильного вероятностного распределения — важный шаг при проведении анализа данных. Распределение выбирается в зависимости от типа и свойств случайной величины, которую нужно исследовать. Правильный выбор распределения позволяет получить более точные результаты и сделать правильные выводы на основе анализа данных.

Методы оценки параметров распределения

Методы оценки параметров распределения являются одним из основных инструментов математической статистики. Они позволяют приблизительно определять параметры случайной величины на основе её выборки.

Одним из наиболее распространенных методов оценки параметров является метод максимального правдоподобия. Суть этого метода заключается в том, что для определения параметров распределения выбирается такой набор значений, при котором функция правдоподобия (вероятность получения данной выборки при определенных значениях параметров) принимает максимальное значение.

Другими методами оценки параметров являются методы моментов и метод Байеса. Метод моментов основан на равенстве теоретических и выборочных моментов распределения, а метод Байеса использует байесовскую статистику для вычисления апостериорного распределения параметров при известном априорном распределении.

Важно понимать, что все методы оценки параметров не дают гарантии на точность определения параметров распределения и требуют достаточно большого объема выборки для получения достоверных результатов.

• Метод максимального правдоподобия — метод определения параметров распределения, основывающийся на выборе такого набора значений, при котором функция правдоподобия принимает максимальное значение.
• Метод моментов — метод определения параметров распределения на основе равенства теоретических и выборочных моментов.
• Метод Байеса — метод определения параметров распределения, использующий байесовскую статистику для вычисления апостериорного распределения параметров.

Все методы оценки параметров имеют свои преимущества и недостатки и выбор метода зависит от типа данных и целей исследования.

Методы проверки статистических гипотез

Одним из основных задач математической статистики является проверка статистических гипотез. Гипотеза – это утверждение о параметрах распределения или зависимостях в исследуемой выборке.

Для проверки гипотез применяются различные статистические методы. Рассмотрим некоторые из них:

• Критерий Стьюдента – используется для проверки гипотез о равенстве средних значений двух выборок. Основан на определении t-статистики и сравнении ее значения с табличным.
• Критерий Хи-квадрат – применяется для проверки гипотез о распределении наблюдаемых частот в выборке. Сравниваются наблюдаемые частоты с ожидаемыми, рассчитанными на основе теоретических предположений.
• Критерий Фишера – используется для проверки гипотез о равенстве дисперсий двух выборок. Вычисляется F-статистика, которая сравнивается с критическим значением.

При использовании любого из методов проверки гипотез необходимо определить уровень значимости и выбрать соответствующий критический уровень. Если значение статистики превышает критическое, гипотеза отвергается.

Пример использования критерия СтьюдентаВыборка 1Выборка 2Среднее значение

10	15	12.5
11	9
12	20
13	11
14	13
	17
	18
	17
	15
	16

Например, для выборок из таблицы мы можем проверить гипотезу о равенстве средних значений. Уровень значимости выберем 0,05. Посчитаем выборочное среднее для каждой выборки и вычислим t-статистику. Если ее значение окажется меньше критического, то гипотеза о равенстве средних значений не отвергается.

Множественная проверка гипотез

Метод множественной проверки гипотез применяется в случае, когда необходимо проверить не одну, а несколько гипотез одновременно. В таком случае вероятность ошибки первого рода может значительно увеличиться, что может привести к неверному отвержению верных гипотез. Для решения этой проблемы используются специальные методы, такие как поправка Бонферрони, метод Холма и другие.

Поправка Бонферрони заключается в том, чтобы снизить уровень значимости для каждой гипотезы, чтобы общий уровень значимости не превышал заданного значения. Для этого уровень значимости сначала умножается на количество проверяемых гипотез, а затем сравнивается с критическим значением соответствующего распределения.

Метод Холма позволяет более эффективно использовать информацию о связи между гипотезами. Он представляет собой последовательную процедуру проверки гипотез в порядке убывания их уровней значимости. Если гипотеза не отвергнута, то проверка останавливается, а уровень значимости для оставшихся гипотез корректируется. Таким образом, метод Холма позволяет достичь более точных результатов при множественной проверке гипотез.

• Примером применения множественной проверки гипотез может служить исследование связи между несколькими факторами и результатом исследования. В таком случае необходимо провести проверку гипотезы о связи для каждого фактора. Применение методов множественной проверки гипотез позволит получить более точные результаты при минимальном уровне ошибки.
• Важно помнить, что применение множественной проверки гипотез не исключает возможности ложных результатов и требует осторожного исследования и интерпретации результатов.

Регрессионный анализ и корреляционный анализ

Регрессионный анализ — это метод математической статистики для оценки влияния факторов на изучаемую переменную. Регрессионный анализ находит отношения между переменными, предсказывает значения зависимых переменных для определенных значений независимых переменных и оценивает уровень статистической значимости этих отношений. Используя регрессионный анализ, можно определить, как изменения в независимых переменных влияют на изменения в зависимых переменных.

Корреляционный анализ — это метод определения степени связи между двумя количественными переменными. Корреляционный анализ позволяет исследователям выявить прямую или обратную связь между двумя переменными. В этом методе используется коэффициент корреляции, который может принимать значения от -1 до 1. Значение близкое к 0 указывает на отсутствие связи, значение близкое к 1 на прямую связь, а значение близкое к -1 на обратную связь.

Регрессионный анализ и корреляционный анализ взаимосвязаны друг с другом. Коэффициент корреляции можно использовать, чтобы охарактеризовать силу и направление связи между зависимой и одной или несколькими независимыми переменными. Кроме того, регрессионный анализ может использоваться для построения уравнения, которое предсказывает значение зависимой переменной в зависимости от значений одной или нескольких независимых переменных.

На практике исследователи часто используют оба метода одновременно, чтобы получить точное понимание связей между переменными. Например, в экономических исследованиях может быть использован регрессионный анализ для оценки влияния изменения процентной ставки на инфляцию, а коэффициент корреляции может использоваться для изучения связи между инфляцией и процентной ставкой, с учетом других факторов, таких как ВВП или безработица.

Видео по теме:

Вопрос-ответ:

Какова основная цель математической статистики?

Основная цель математической статистики — извлечение выводов о реальном мире из данных, которые никогда не даются чистыми. Методы математической статистики обнаруживают знаковые закономерности и различия в данных, позволяя исследователям сделать выводы о том, какие факторы могут влиять на исследуемый процесс или явление, и предсказать будущие события на основе таких выводов.

Какие методы анализа данных используются в математической статистике?

В математической статистике используется множество методов, таких как статистический анализ данных, регрессионный анализ, дисперсионный анализ, кластерный анализ, байесовский анализ и т. д. Каждый из этих методов может использоваться для решения различных типов задач по анализу данных, таких как выявление взаимосвязей между переменными, прогнозирование результатов, классификация объектов и т. д.

Какие данные используются в математической статистике?

Данные, используемые в математической статистике, могут быть как количественными (например, возраст, рост, вес), так и качественными (например, пол, цвет глаз, регион проживания). Кроме того, данные могут быть непрерывными, дискретными или порядковыми. Например, время, необходимое для выполнения задачи, является непрерывной переменной, а количество задач, выполненных студентом, является дискретной.

Как выбрать подходящий метод математической статистики?

Выбор подходящего метода математической статистики зависит от конкретной задачи и свойств данных, которые необходимо анализировать. При выборе метода следует учитывать тип данных, количество переменных, объем выборки, распределение данных, наличие выбросов и пропусков, цель анализа, а также сложность модели.

Какие примеры использования математической статистики можно привести?

Методы математической статистики используются во многих областях, таких как экономика, биология, медицина, физика, политология и т. д. Например, математическая статистика может помочь предсказать поведение финансовых рынков, определить эффективность лекарств и проанализировать результаты опросов.

Как работает дисперсионный анализ?

Дисперсионный анализ используется для сравнения средних значений между группами данных. Он позволяет выявить различия между группами и оценить статистическую значимость этих различий. Для этого сначала вычисляется общая дисперсия выборки и дисперсии внутри каждой группы. Затем вычисляется статистика F, которая показывает отношение между дисперсией между группами и дисперсиями внутри групп. Если F превышает критический уровень значимости, можно заключить, что средние значения между группами различаются.

Какие преимущества использования методов математической статистики?

Преимущества использования методов математической статистики включают лучшее понимание данных и тенденций, повышение точности прогнозирования будущих событий, обнаружение факторов, влияющих на исследуемый процесс или явление, определение статистической значимости результатов, возможность проверить гипотезы и т. д. Кроме того, использование математической статистики может помочь сократить затраты времени и ресурсов, улучшить принятие решений и повысить качество результатов исследования.

Методы машинного обучения на основе математической статистики

Машинное обучение – это метод анализа данных, который использует алгоритмы для извлечения информации из больших объемов данных. Математическая статистика занимается разработкой и применением математических методов для обработки данных и описания вероятностных закономерностей в данных.

Методы машинного обучения на основе математической статистики используются для прогнозирования, классификации, кластеризации, анализа данных и других задач. Они могут быть основаны на различных алгоритмах, таких как регрессия, деревья решений, нейронные сети, метод опорных векторов и другие.

Одним из самых известных методов машинного обучения на основе математической статистики является метод наименьших квадратов. Он используется для построения модели, которая наилучшим образом соответствует набору данных.

Другим методом является байесовский классификатор. Он использует теорему Байеса для вычисления вероятности того, что объект принадлежит определенному классу.

• Метод максимального правдоподобия — используется для оценки параметров модели на основе наблюдаемых данных.
• Метод дискриминантного анализа — используется для поиска различий между группами объектов.

Использование методов машинного обучения на основе математической статистики позволяет автоматизировать процесс анализа данных и повысить точность результатов. Однако выбор метода зависит от цели и типа данных, поэтому важно правильно выбрать метод для конкретной задачи.

Примеры применения математической статистики в реальной жизни

Математическая статистика позволяет решать множество задач в реальной жизни. Например, оценивать риски, принимать решения на основе имеющихся данных и прогнозировать будущие события.

Один из примеров применения математической статистики — это изучение социально-экономических процессов в государстве. На основе данных о населении, доходах, безработице, инфляции и других факторах можно оценить текущую экономическую ситуацию и прогнозировать ее развитие в будущем.

Еще один пример применения математической статистики — это медицина. С помощью анализа больших объемов медицинских данных можно выявить закономерности протекания заболеваний и способы их лечения. Например, данные могут использоваться для нахождения оптимальной дозировки лекарственных средств или оценки эффективности новых методов лечения.

Математическая статистика также применяется в бизнесе. Она помогает выявлять закономерности продаж, определять популярность товаров или услуг, оценивать эффективность маркетинговых кампаний и так далее.

В целом, математическая статистика — это мощный инструмент для решения различных задач в реальной жизни. Она может использоваться в различных областях, помогая принимать рациональные решения на основе имеющихся данных.