Что такое мгновенная скорость в математике

Мгновенная скорость в математике — это значение скорости объекта в конкретный момент времени. Узнайте, как она рассчитывается и как она отличается от средней скорости.

В математике мгновенная скорость — это концепция, которая используется для определения скорости объекта в определенный момент времени. Она является основным понятием в дифференциальном исчислении и позволяет измерять изменение положения объекта в зависимости от времени в данной точке.

Определение мгновенной скорости связано с понятием предела. Если предел скорости объекта приближается к определенному значению приближающегося времени, то это значение и будет мгновенной скоростью объекта в данной точке.

Например, представим себе автомобиль, движущийся с постоянной скоростью на трассе. Если мы зафиксируем определенный момент времени, то мгновенная скорость автомобиля в этот момент будет равна его текущей скорости.

Мгновенная скорость имеет большое значение в физике, где она позволяет определить ускорение тела и понять его движение в пространстве. Она также имеет важное применение в экономике и финансах, где позволяет анализировать изменения цен и стоимости акций в определенный момент времени.

Определение мгновенной скорости

Математически мгновенная скорость можно выразить следующим образом:

v = lim Δs/Δt → 0

Где:

• v — мгновенная скорость
• Δs — изменение пути
• Δt — изменение времени
• lim — предел функции при стремлении аргумента к определенному значению

Мгновенная скорость позволяет нам определить скорость движения объекта в конкретный момент времени, игнорируя все промежуточные значения. Например, при измерении скорости автомобиля на дороге мгновенная скорость покажет, как быстро автомобиль движется в данный момент, не учитывая скорость в прошлые или будущие моменты времени.

Определение мгновенной скорости играет важную роль в физике и математике, особенно при рассмотрении движения объектов. Оно позволяет нам более точно описывать и анализировать процессы, происходящие в мире вокруг нас.

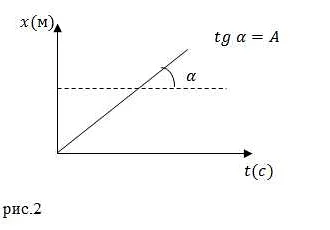
Формула мгновенной скорости

Мгновенная скорость в математике определяется как производная функции перемещения по времени. Другими словами, это скорость точки на графике функции в определенный момент времени.

Формально, мгновенная скорость v(t) может быть выражена следующей формулой:

v(t) = limΔt→0 (Δx / Δt)

Где Δt представляет собой бесконечно малый интервал времени, а Δx — соответствующее изменение позиции за этот интервал времени.

Таким образом, формула мгновенной скорости позволяет нам вычислить скорость в любой момент времени, построив предел отношения изменения позиции к изменению времени при стремлении Δt к нулю.

Пример:

Допустим, что функция перемещения x(t) дана следующим образом: x(t) = 2t^2 + 3t + 1. Чтобы найти мгновенную скорость в момент времени t = 2, мы можем использовать формулу мгновенной скорости.

Сначала вычислим производную функции x(t): dx(t) / dt = 4t + 3.

Затем подставим t = 2 в полученное выражение: dx(2) / dt = 4(2) + 3 = 11.

Таким образом, мгновенная скорость в момент времени t = 2 равна 11.

Пример расчета мгновенной скорости

Чтобы найти мгновенную скорость объекта в определенный момент времени, нам необходимо найти производную функции пути s(t) по времени. В данном случае, производная будет равна:

s'(t) = 4t — 3

Теперь, чтобы найти мгновенную скорость в определенный момент времени, подставим значение времени в производную функции:

Допустим, нам нужно найти мгновенную скорость в момент времени t = 2 секунды. Подставив это значение в производную функции, получим:

s'(2) = 4 * 2 — 3 = 5

Таким образом, мгновенная скорость объекта в момент времени t = 2 секунды будет равна 5 м/с.

Интерпретация мгновенной скорости

Мгновенная скорость в математике представляет собой показатель, который определяет, как быстро движется объект в определенный момент времени. Она может быть интерпретирована как скорость объекта в данный момент времени, когда произошло измерение.

Интерпретация мгновенной скорости может быть проиллюстрирована следующим примером: представим себе автомобиль, движущийся по шоссе. В течение всего пути от точки А до точки Б, автомобиль может изменять свою скорость. В каждый момент времени можно измерить его мгновенную скорость, например, при помощи спидометра. Итак, если мы измерим скорость автомобиля в точке А, то получим его мгновенную скорость в этот момент времени.

Мгновенная скорость может быть представлена численно и графически. Например, если мы построим график зависимости скорости автомобиля от времени, то в каждый момент времени можно будет найти точку на графике, которая соответствует его мгновенной скорости. Таким образом, график позволяет наглядно представить изменение скорости объекта с течением времени.

Интерпретация мгновенной скорости важна не только в математике, но и в физике, где она используется для анализа движения объектов и определения их ускорения. Мгновенная скорость предоставляет информацию о том, как быстро объект движется в данный момент времени, что позволяет более точно описывать его движение и предсказывать его будущее положение.

Связь мгновенной скорости и средней скорости

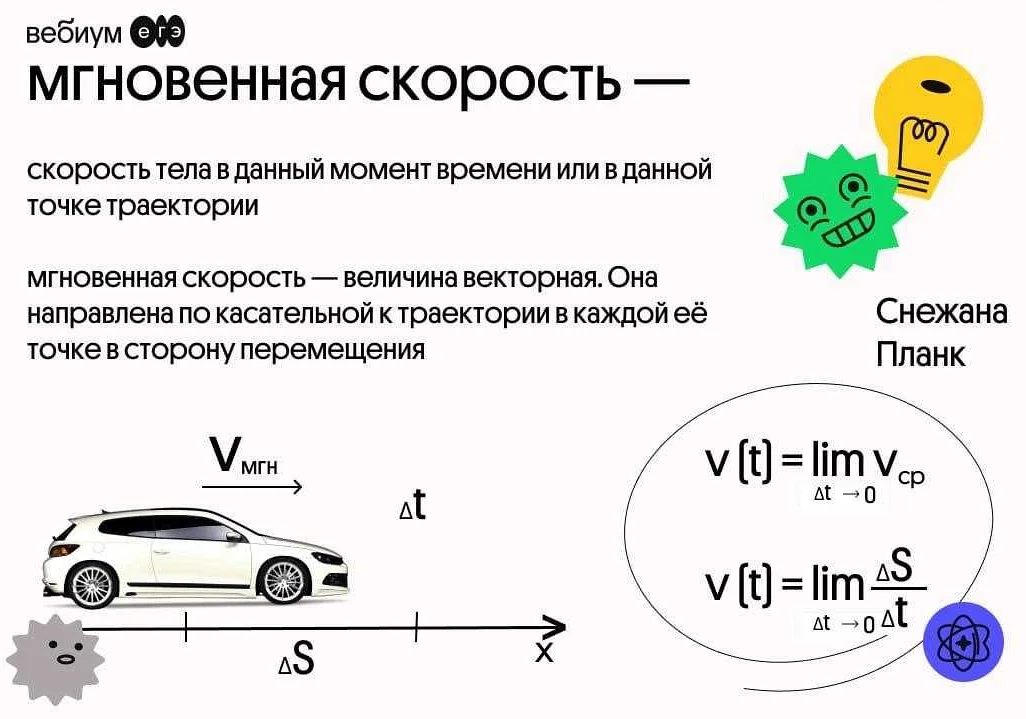
Мгновенная скорость может быть представлена как предел средней скорости, когда интервал времени стремится к нулю. То есть, если мы уменьшаем интервал времени, близкий к нулю, мы получаем все более точную оценку мгновенной скорости.

Например, представим себе автомобиль, движущийся по трассе. Средняя скорость автомобиля может быть рассчитана, разделив пройденное расстояние на затраченное время. Однако, мгновенная скорость автомобиля может быть определена только в определенный момент времени, например, когда мы измеряем скорость с помощью спидометра.

Таким образом, мгновенная скорость и средняя скорость взаимосвязаны: мгновенная скорость является пределом средней скорости при стремлении интервала времени к нулю.

Практическое применение мгновенной скорости

Мгновенная скорость имеет широкое практическое применение в различных областях науки и техники. Ниже приведены несколько примеров использования мгновенной скорости:

1. Физика: Мгновенная скорость используется в физике для изучения движения тела. Она позволяет определить скорость объекта в конкретный момент времени, что помогает в анализе динамики и кинематики систем.
2. Астрономия: Мгновенная скорость играет важную роль в астрономии при изучении движения планет, звезд и других небесных объектов. Она позволяет определить точное положение и скорость объекта в заданный момент времени.
3. Инженерия: В инженерии мгновенная скорость используется для анализа движения механических систем. Это помогает инженерам прогнозировать поведение объектов и оптимизировать их производительность.
4. Транспорт: Мгновенная скорость играет важную роль в сфере транспорта. Она используется для определения мгновенного положения и скорости транспортных средств, что позволяет улучшить безопасность дорожного движения и эффективность перевозок.
5. Медицина: В медицине мгновенная скорость применяется для анализа движения органов и тканей в организме человека. Она помогает в диагностике и лечении различных заболеваний, а также в разработке реабилитационных программ.

Это лишь некоторые примеры практического применения мгновенной скорости. В реальном мире она находит применение практически во всех областях, требующих изучения и анализа движения объектов.

Вопрос-ответ:

Что такое мгновенная скорость в математике?

Мгновенная скорость в математике — это скорость тела в определенный момент времени. Она рассчитывается как предел отношения изменения пройденного пути к изменению времени в этот момент.

Как определить мгновенную скорость?

Мгновенную скорость можно определить, найдя предел отношения изменения пройденного пути к изменению времени в определенный момент. Для этого нужно разделить очень маленькое изменение пройденного пути на очень маленькое изменение времени вокруг этого момента.

Какие примеры можно привести для понимания мгновенной скорости?

Примером мгновенной скорости может быть автомобиль, который движется по дороге. Мгновенная скорость в данном случае может быть рассчитана как предел отношения изменения пройденного расстояния к изменению времени в конкретный момент.

Как мгновенная скорость связана с средней скоростью?

Мгновенная скорость может быть рассчитана как предел отношения изменения пройденного пути к изменению времени в конкретный момент. Средняя скорость, с другой стороны, рассчитывается как отношение пройденного пути к затраченному времени за всё время движения. Мгновенная скорость является мгновенным значением средней скорости.

Зачем нужно знать мгновенную скорость в математике?

Знание мгновенной скорости в математике важно для решения различных задач, связанных с движением тела. Она позволяет определить точную скорость тела в определенный момент времени, что может быть полезно при моделировании и анализе различных физических процессов.

Что такое мгновенная скорость в математике?

Мгновенная скорость в математике — это скорость изменения положения объекта в определенный момент времени. Она представляет собой предел отношения изменения положения к изменению времени, когда интервал времени стремится к нулю.

Как определить мгновенную скорость?

Для определения мгновенной скорости необходимо вычислить предел отношения изменения положения объекта к изменению времени при стремлении интервала времени к нулю. Это можно сделать, используя дифференцирование функции положения по времени.

Ограничения использования мгновенной скорости

Однако использование мгновенной скорости имеет свои ограничения:

1. Точность измерений: Чтобы правильно определить мгновенную скорость, необходимо иметь точные измерения положения и времени. Даже небольшие ошибки в измерениях могут привести к неточным результатам.

2. Непрерывность движения: Мгновенная скорость применима только к непрерывному движению объекта. Если объект движется с прерывистыми скачками или изменяет свое направление, мгновенная скорость может стать неопределенной.

3. Единство измерения: Мгновенная скорость измеряется в единицах расстояния, деленного на единицу времени, например, метров в секунду. Это ограничивает использование мгновенной скорости для объектов, движущихся с очень большими или очень малыми скоростями, для которых требуются другие единицы измерения.

Важно помнить, что мгновенная скорость — это идеализированная концепция, которая учитывает только изменение положения объекта в конкретный момент времени. Для анализа движения в целом может потребоваться использование других показателей скорости, таких как средняя скорость.

Видео по теме: