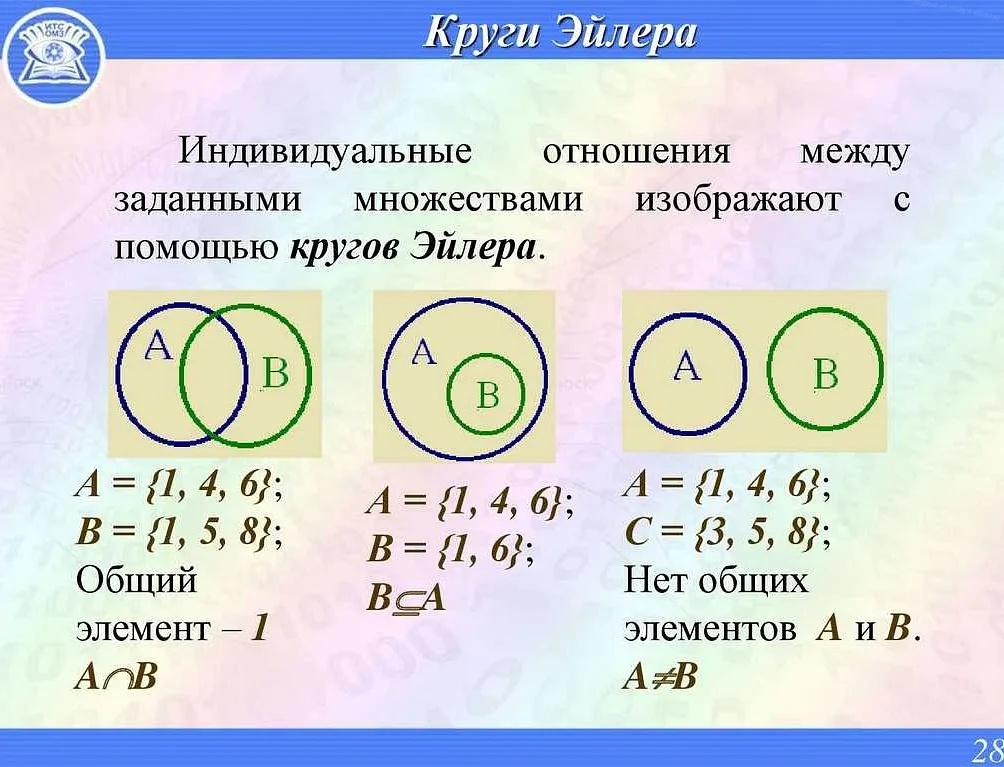
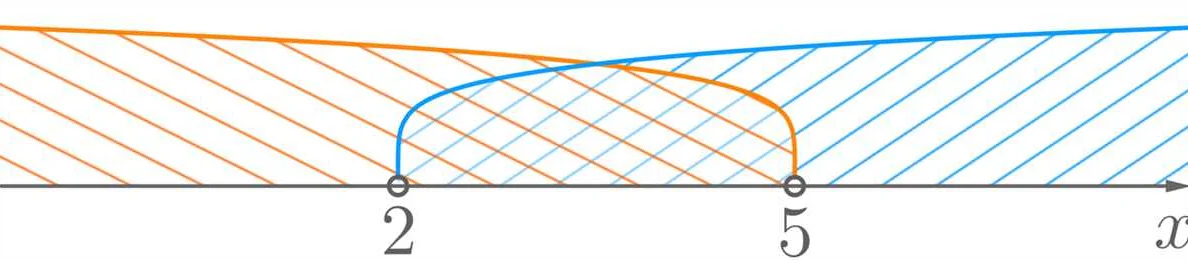
Что такое множество в математике 1 класс

Множество в математике 1 класс – это группа объектов, которые объединены общим признаком. В данной статье вы узнаете, как определить и описать множество, а также как решать задачи на работу с множествами в начальной школе.

В математике множество — это совокупность объектов, которые объединены общим свойством или признаком. Множество может состоять из любого количества элементов, которые могут быть числами, буквами, словами или другими объектами.

Определение множества можно представить следующим образом: если у нас есть какой-то набор объектов, то мы можем объединить их в одно множество, записывая все элементы между фигурными скобками и разделяя их запятой.

Пример: множество цифр от 1 до 5 можно записать следующим образом: {1, 2, 3, 4, 5}.

Множество может быть пустым, то есть не содержать ни одного элемента. В таком случае мы записываем его как {} или ∅. Например, пустое множество букв английского алфавита можно записать как {}.

Важными понятиями в теории множеств являются элементы множества и принадлежность. Если какой-то объект является элементом множества, то мы говорим, что он принадлежит этому множеству.

Что такое множество в математике?

Основные понятия, связанные с множествами, включают:

• Элементы множества: это отдельные объекты или значения, которые составляют множество.
• Пустое множество: это множество, которое не содержит ни одного элемента. Оно обозначается символом Ø или {}.
• Равенство множеств: два множества считаются равными, если они содержат одни и те же элементы.
• Подмножество: множество A является подмножеством множества B, если все элементы множества A также являются элементами множества B.
• Мощность множества: количество элементов в множестве называется его мощностью. Мощность множества A обозначается символом |A|.

Множества используются в математике для классификации объектов, упрощения выражений и решения задач. Они являются одной из основных концепций в математике и используются во многих разделах этой науки, включая алгебру, геометрию и теорию вероятностей.

Видео по теме:

Основные понятия множества

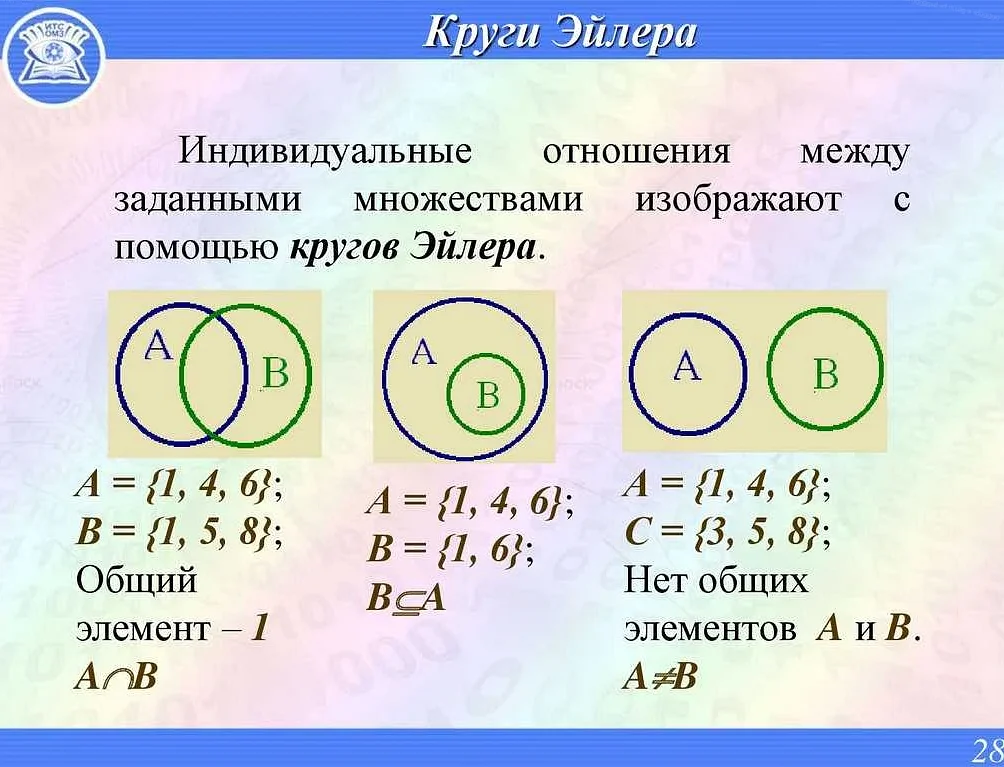
Элементы множества могут быть числами, буквами, словами или любыми другими объектами. Каждый элемент множества может встречаться в нем только один раз.

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается символом ∅ или {}.

Если элемент a принадлежит множеству A, то пишут a ∈ A. Если элемент b не принадлежит множеству B, то пишут b ∉ B.

Если все элементы множества A являются также элементами множества B, то говорят, что A является подмножеством B и пишут A ⊆ B. Если хотя бы один элемент множества C не принадлежит множеству D, то говорят, что C не является подмножеством D и пишут C ⊈ D.

Мощностью (количеством элементов) множества называется число элементов, принадлежащих данному множеству. Мощность множества A обозначается символом |A|.

Множество может быть конечным или бесконечным. Конечное множество имеет определенное количество элементов, а бесконечное множество содержит бесконечное число элементов.

Множества могут быть эквивалентными, если они содержат одинаковое количество элементов. Такие множества называются равномощными.

Элементы множества

Примеры элементов множества:

• Множество натуральных чисел: {1, 2, 3, 4, 5, …}
• Множество гласных букв: {а, е, ё, и, о, у, э, ю, я}
• Множество дней недели: {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}
• Множество цветов радуги: {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый}

Вопрос-ответ:

Что такое множество?

Множество в математике — это группа или набор элементов, объединенных по какому-то признаку.

Как определить множество?

Множество можно определить, перечислив его элементы внутри фигурных скобок. Например, {1, 2, 3} — множество из трех элементов.

Какие бывают примеры множеств?

Примеры множеств: {красный, синий, желтый} — множество цветов, {кот, собака, птица} — множество животных.

Какие свойства имеют множества?

Множества могут быть конечными или бесконечными, содержать одинаковые элементы или быть пустыми.

Почему множество важно в математике?

Множество является основным понятием в математике и используется для решения различных задач и построения других математических объектов.

Что такое множество?

Множество в математике — это группа или коллекция объектов, которые объединены общим свойством.

Пустое множество

Пустое множество является основным понятием в теории множеств и играет важную роль во многих математических концепциях и доказательствах.

Например, если у нас есть множество всех студентов в классе, то пустое множество будет представлять собой ситуацию, когда в классе нет ни одного студента.

Пустое множество не содержит элементов и является особым случаем множества. Оно может быть использовано в различных операциях с множествами, таких как объединение, пересечение, разность и дополнение.

Например, объединение пустого множества с любым другим множеством даст в результате то же самое множество.

Примеры множеств

Например, рассмотрим множество «Цвета радуги». Оно содержит элементы: красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый.

Другой пример множества — «Числа от 1 до 10». В этом множестве содержатся следующие элементы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10.

Также можно рассмотреть множество «Дни недели». Оно содержит элементы: понедельник, вторник, среда, четверг, пятница, суббота и воскресенье.

Множество «Фрукты» включает в себя элементы: яблоко, груша, банан, апельсин, мандарин и виноград.

И наконец, рассмотрим множество «Буквы алфавита». Оно содержит все буквы русского алфавита: а, б, в, г, д, е, ё, ж, з, и, й, к, л, м, н, о, п, р, с, т, у, ф, х, ц, ч, ш, щ, ъ, ы, ь, э, ю, я.

Это лишь некоторые примеры множеств. В математике и в реальной жизни множества находят широкое применение.

Множество цветов радуги

Радуга — это феномен, который возникает при попадании солнечного света на капли воды в атмосфере. Она представляет собой полукруглую дугу из разноцветных полос, которые идут в следующем порядке: красный, оранжевый, желтый, зеленый, голубой, синий и фиолетовый. Именно эти семь цветов образуют множество цветов радуги.

Множество цветов радуги является конечным множеством, так как содержит определенное количество элементов — семь цветов. Каждый элемент множества — это определенный цвет, который имеет свою характеристику и отличается от других цветов радуги.

Множество цветов радуги в математике можно представить в виде списка:

Множество цветов радуги = {красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый}

Таким образом, множество цветов радуги — это совокупность семи различных цветов, которые можно наблюдать при наличии солнечного света и капель воды в атмосфере. Это интересное и красочное множество, которое можно изучать в контексте математики и природных явлений.

Множество букв русского алфавита

Множество букв русского алфавита состоит из 33 символов. Каждая буква представляет собой отдельный элемент этого множества. Буквы русского алфавита используются для написания русского языка и имеют свои названия и звуковое значение.

Вот полный список букв русского алфавита:

• А
• Б
• В
• Г
• Д
• Е
• Ё
• Ж
• З
• И
• Й
• К
• Л
• М
• Н
• О
• П
• Р
• С
• Т
• У
• Ф
• Х
• Ц
• Ч
• Ш
• Щ
• Ъ
• Ы
• Ь
• Э
• Ю
• Я

Эти буквы можно использовать для создания различных слов и предложений на русском языке. Изучение букв русского алфавита является одним из первых шагов в обучении грамоте и чтению.

Множество дни недели

Множество дни недели включает в себя следующие элементы:

• Понедельник
• Вторник
• Среда
• Четверг
• Пятница
• Суббота
• Воскресенье

Каждый день недели является отдельным элементом множества. Эти элементы могут быть собраны вместе и образовывать множество дни недели.

Множество дни недели полезно для описания повторяющихся событий или распределения активностей на разные дни недели.