Натуральное число это в математике что такое

Натуральное число — это важная концепция в математике, оно обозначает положительное целое число, которое используется для подсчета, упорядочивания и множественных операций. Узнайте, что такое натуральные числа и как они играют важную роль в различных областях математики и ежедневной жизни.

Натуральное число — это однопорядковое число, используемое для подсчета и измерений. В математике натуральные числа обозначаются символом N и включают положительные целые числа, начиная с единицы и продолжая бесконечно. Они являются основой для строительства других множеств чисел и имеют ряд свойств, которые помогают в изучении математических операций.

Натуральные числа имеют несколько основных свойств. Во-первых, они образуют бесконечную последовательность чисел, которая начинается с 1 и постепенно увеличивается на единицу. Во-вторых, натуральные числа не могут быть отрицательными или дробными. Они используются для подсчета количества объектов и величин, которые могут быть представлены целыми числами.

Натуральные числа можно использовать для решения различных математических задач. Они позволяют нам считать предметы, измерять расстояния и временные интервалы, а также выполнять арифметические операции, такие как сложение, вычитание, умножение и деление. Благодаря своим свойствам, натуральные числа играют важную роль в разных областях науки и жизни.

Что такое натуральное число

Натуральные числа имеют несколько свойств:

Свойство	Описание
Закон сложения	Если a и b — натуральные числа, то a + b также является натуральным числом.
Закон умножения	Если a и b — натуральные числа, то a * b также является натуральным числом.
Ассоциативность сложения	Для любых натуральных чисел a, b и c справедливо: (a + b) + c = a + (b + c).
Ассоциативность умножения	Для любых натуральных чисел a, b и c справедливо: (a * b) * c = a * (b * c).
Коммутативность сложения	Для любых натуральных чисел a и b справедливо: a + b = b + a.
Коммутативность умножения	Для любых натуральных чисел a и b справедливо: a * b = b * a.

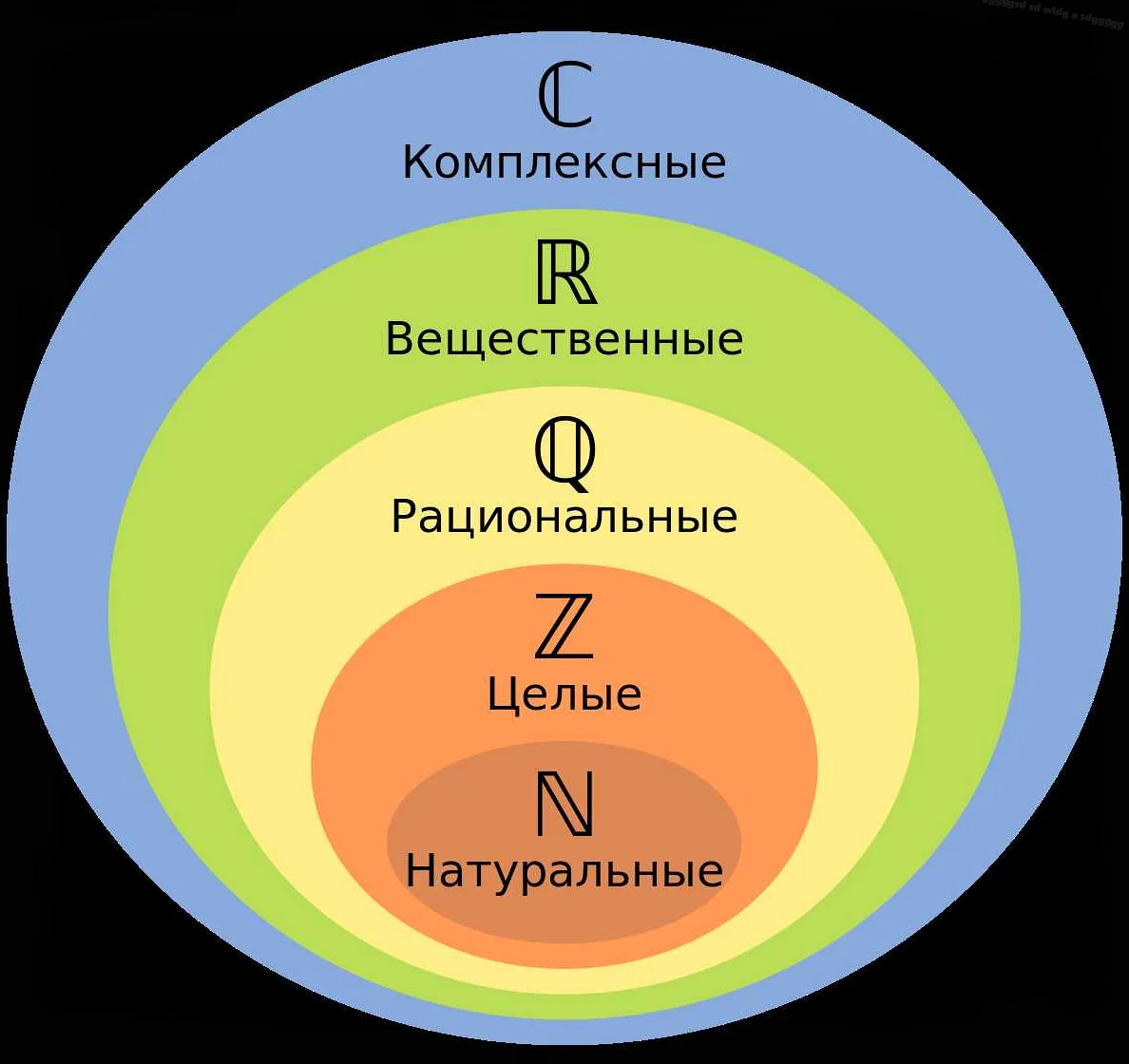
Натуральные числа являются одной из основных и наиболее изучаемых областей в математике. Они являются основой для построения других множеств чисел, таких как целые, рациональные и действительные числа.

Примеры натуральных чисел

Вот некоторые примеры натуральных чисел:

1	единица
2	два
3	три
4	четыре
5	пять
6	шесть
7	семь
8	восемь
9	девять
10	десять

Эти числа можно использовать для различных целей, таких как обозначение количества предметов, нумерация страниц, учет времени и т.д.

Свойства натуральных чисел

Натуральные числа обладают рядом важных свойств, которые помогают нам работать с ними и решать математические задачи. Вот некоторые из них:

1. Замкнутость относительно сложения и умножения: если сложить или умножить два натуральных числа, то результат также будет натуральным числом. Например, сумма 3 и 5 равна 8, а произведение 4 и 7 равно 28.
2. Существование нейтральных элементов: для сложения нейтральным элементом является число 0, так как при сложении нуля с любым числом получается это же число. Для умножения нейтральным элементом является число 1, так как при умножении любого числа на 1 получается это же число.
3. Свойство ассоциативности: сложение и умножение натуральных чисел ассоциативны, то есть порядок, в котором мы выполняем операции, не влияет на результат. Например, для трех чисел a, b и c выполняется равенство (a + b) + c = a + (b + c) и (a * b) * c = a * (b * c).
4. Свойство коммутативности: сложение и умножение натуральных чисел коммутативны, то есть порядок, в котором мы складываем или умножаем числа, не влияет на результат. Например, для двух чисел a и b выполняется равенство a + b = b + a и a * b = b * a.
5. Свойство дистрибутивности: умножение натуральных чисел распределено относительно сложения, то есть a * (b + c) = a * b + a * c. Например, для чисел 2, 3 и 4 выполняется равенство 2 * (3 + 4) = 2 * 3 + 2 * 4.

Эти свойства натуральных чисел используются во многих областях математики и помогают нам проводить различные вычисления и доказывать теоремы.

Простые и составные числа

В математике натуральные числа делятся на два типа: простые и составные.

Простое число — это натуральное число, которое имеет ровно два делителя: 1 и само число. Простые числа начинаются с числа 2 и продолжаются бесконечно. Некоторые примеры простых чисел: 2, 3, 5, 7, 11 и т. д.

Составное число — это натуральное число, которое имеет больше двух делителей. Оно может быть разложено на произведение двух или более простых чисел. Некоторые примеры составных чисел: 4, 6, 8, 9, 10 и т. д.

Простые числа являются основными строительными блоками для всех других чисел. Каждое составное число можно разложить на простые множители. Это называется факторизацией числа.

Простые числаСоставные числа

2	4
3	6
5	8
7	9

Простые числа имеют множество интересных свойств и применений в математике и криптографии. Они являются основой для решения многих задач, таких как поиск наибольшего общего делителя и проверка чисел на простоту.

Сумма и разность натуральных чисел

Пример суммыПример разности

3 + 4 = 7	5 — 2 = 3
6 + 9 = 15	8 — 3 = 5
12 + 7 = 19	10 — 5 = 5

Сумма и разность натуральных чисел обладают следующими свойствами:

• Сумма двух натуральных чисел всегда является натуральным числом.
• Разность двух натуральных чисел может быть натуральным числом или нулем.
• Сумма натуральных чисел ассоциативна: при сложении трех натуральных чисел результат не зависит от порядка слагаемых.
• Разность натуральных чисел не ассоциативна: результат вычитания зависит от порядка чисел.
• Сумма натуральных чисел коммутативна: порядок слагаемых не влияет на результат.
• Разность натуральных чисел не коммутативна: результат вычитания зависит от порядка чисел.

Умножение и деление натуральных чисел

Умножение двух натуральных чисел a и b обозначается символом «×» и определяется следующим образом:

a × b = a + a + … + a (b раз),

то есть умножение числа a на число b равно сумме числа a, взятого b раз.

Например, умножение числа 3 на 4 можно записать так: 3 × 4 = 3 + 3 + 3 + 3 = 12.

Деление двух натуральных чисел a и b обозначается символом «÷» и определяется следующим образом:

a ÷ b = c,

где c — натуральное число, которое является частным от деления числа a на число b, и при этом выполняется условие:

a = b × c + r,

где r — натуральное число, которое называется остатком от деления числа a на число b.

Например, деление числа 10 на 3 можно записать так: 10 ÷ 3 = 3, при этом остаток от деления равен 1: 10 = 3 × 3 + 1.

Умножение и деление натуральных чисел обладают рядом свойств, таких как ассоциативность, коммутативность и дистрибутивность, которые можно изучить более подробно в теории чисел.

Остаток от деления натуральных чисел

Остаток от деления двух натуральных чисел a и b определяется следующим образом: если a делится нацело на b, то остаток от деления равен нулю. В противном случае, остаток от деления является положительным числом, меньшим чем b.

Остаток от деления можно вычислить с помощью таблицы деления. В таблице деления нужно записать последовательные результаты вычитания более меньшего числа из более большего, пока результат вычитания не станет меньше делителя. Остаток от деления будет равен последнему вычитанию в таблице.

ДелимоеДелительЧастноеОстаток

a

b

a / b

a % b

Пример:

ДелимоеДелительЧастноеОстаток

15

4

3

3

В этом примере 15 делится нацело на 4, частное равно 3, а остаток равен 3.

Остаток от деления используется в различных областях математики и программирования, включая алгебру, теорию чисел, криптографию, алгоритмы и многое другое. Он является важным понятием для понимания и решения различных задач.

Степени и корни натуральных чисел

Степень натурального числа обозначается записью an, где число a называется основанием степени, а число n — показателем степени. Например, число 23 означает, что нужно умножить число 2 на себя 3 раза: 2 * 2 * 2 = 8.

Основные свойства степеней натуральных чисел:

1. Если число a возвести в степень 0, то получится 1: a0 = 1.
2. Если число a возвести в степень 1, то получится само число a: a1 = a.
3. Произведение двух степеней с одинаковым основанием равно степени с тем же основанием и суммой показателей: am * an = am+n.
4. Частное двух степеней с одинаковым основанием равно степени с тем же основанием и разностью показателей: am / an = am-n.
5. Степень степени равна степени с тем же основанием и произведением показателей: (am)n = am*n.

Корень натурального числа обозначается записью √a, где число a является радикандом. Например, корень квадратный из числа 9 равен 3, так как 3 * 3 = 9.

Основные свойства корней натуральных чисел:

1. Корень из числа возводится в квадрат, чтобы получить это число: (√a)2 = a.
2. Корень из произведения равен произведению корней: √(a * b) = √a * √b.
3. Корень из частного равен частному корней: √(a / b) = √a / √b.
4. Корень корня равен корню с произведением показателей: (√a)n = √an.

Знание степеней и корней натуральных чисел позволяет проводить различные вычисления и решать задачи в математике и других областях науки.

Видео по теме:

Что такое натуральное число?

Натуральное число — это положительное целое число, которое используется для обозначения количества или порядка. Например, числа 1, 2, 3, 4 и так далее.

Можно ли натуральное число представить в виде десятичной дроби?

Нет, натуральные числа не могут быть представлены в виде десятичных дробей. Они являются целыми числами и не имеют десятичной части.