Что такое натуральные числа в математике 6 класс определение

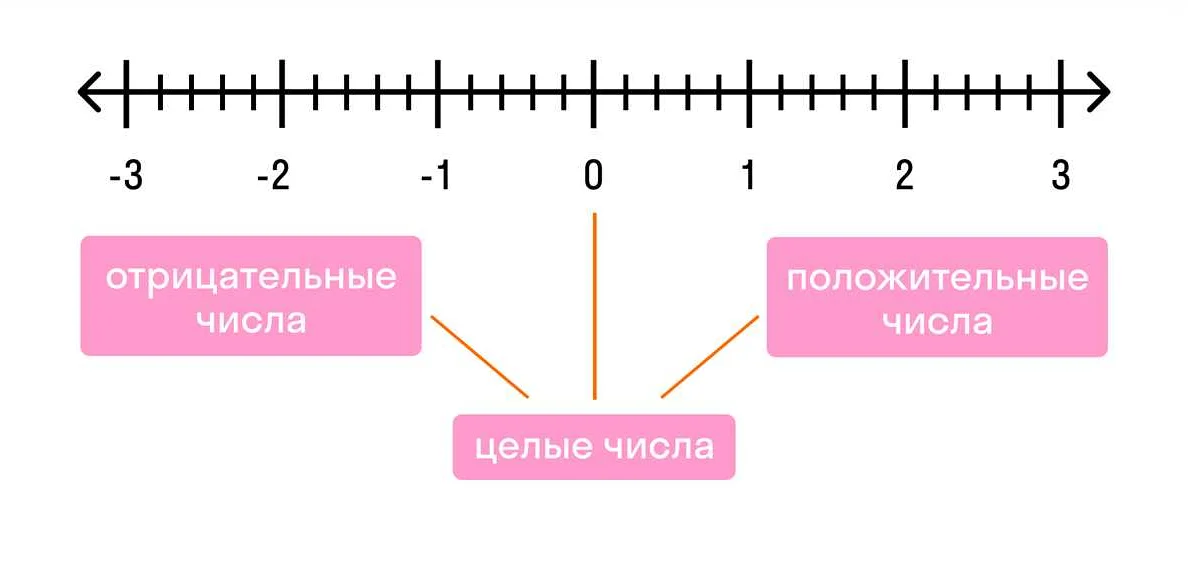
Натуральные числа в математике для 6 класса — это положительные целые числа, которые используются для счета объектов и показывают их количество. В этой статье мы рассмотрим определение натуральных чисел и их основные свойства.

Натуральные числа — это числа, которые используются для обозначения количества элементов в конечном множестве. Они начинаются с единицы и продолжаются бесконечно. В математике натуральные числа обозначаются символом N.

Они являются основой для изучения арифметических операций, таких как сложение, вычитание, умножение и деление. Натуральные числа также играют важную роль в решении различных задач и уравнений.

Основные свойства натуральных чисел включают в себя коммутативность сложения и умножения, ассоциативность сложения и умножения, а также дистрибутивность умножения относительно сложения. Кроме того, натуральные числа обладают свойствами порядка, такими как транзитивность, антисимметричность и рефлексивность.

Натуральные числа играют важную роль в повседневной жизни. Они используются для подсчета предметов, людей, денег и времени. Также они часто встречаются в различных науках, таких как физика, химия, биология и экономика.

Изучение натуральных чисел в 6 классе является важным этапом в математическом образовании каждого ученика. Оно помогает развить навыки логического мышления, абстрактного мышления и анализа данных. Также изучение натуральных чисел позволяет ученикам понять и применять основные свойства чисел в решении задач и уравнений.

Определение натуральных чисел в математике 6 класс

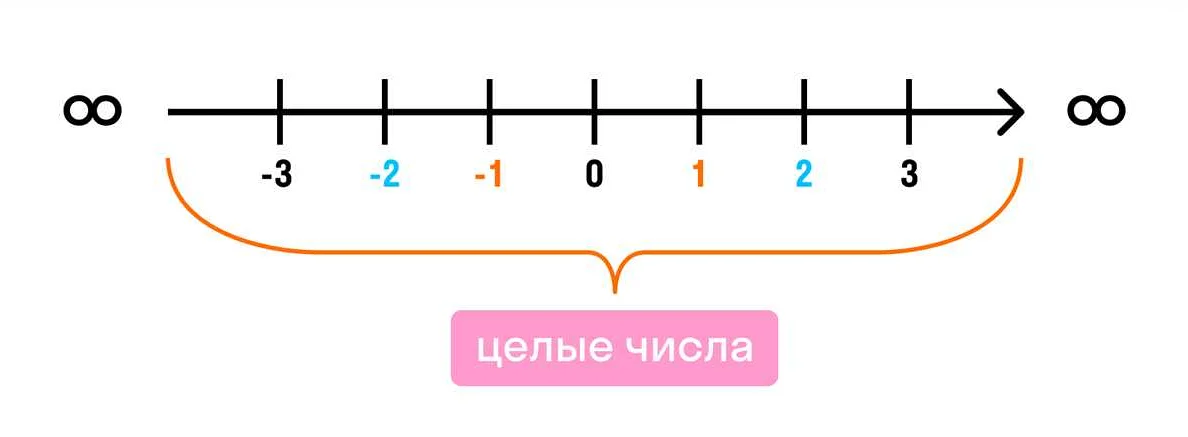
Натуральные числа можно записать в виде упорядоченной последовательности: 1, 2, 3, 4, 5, и так далее.

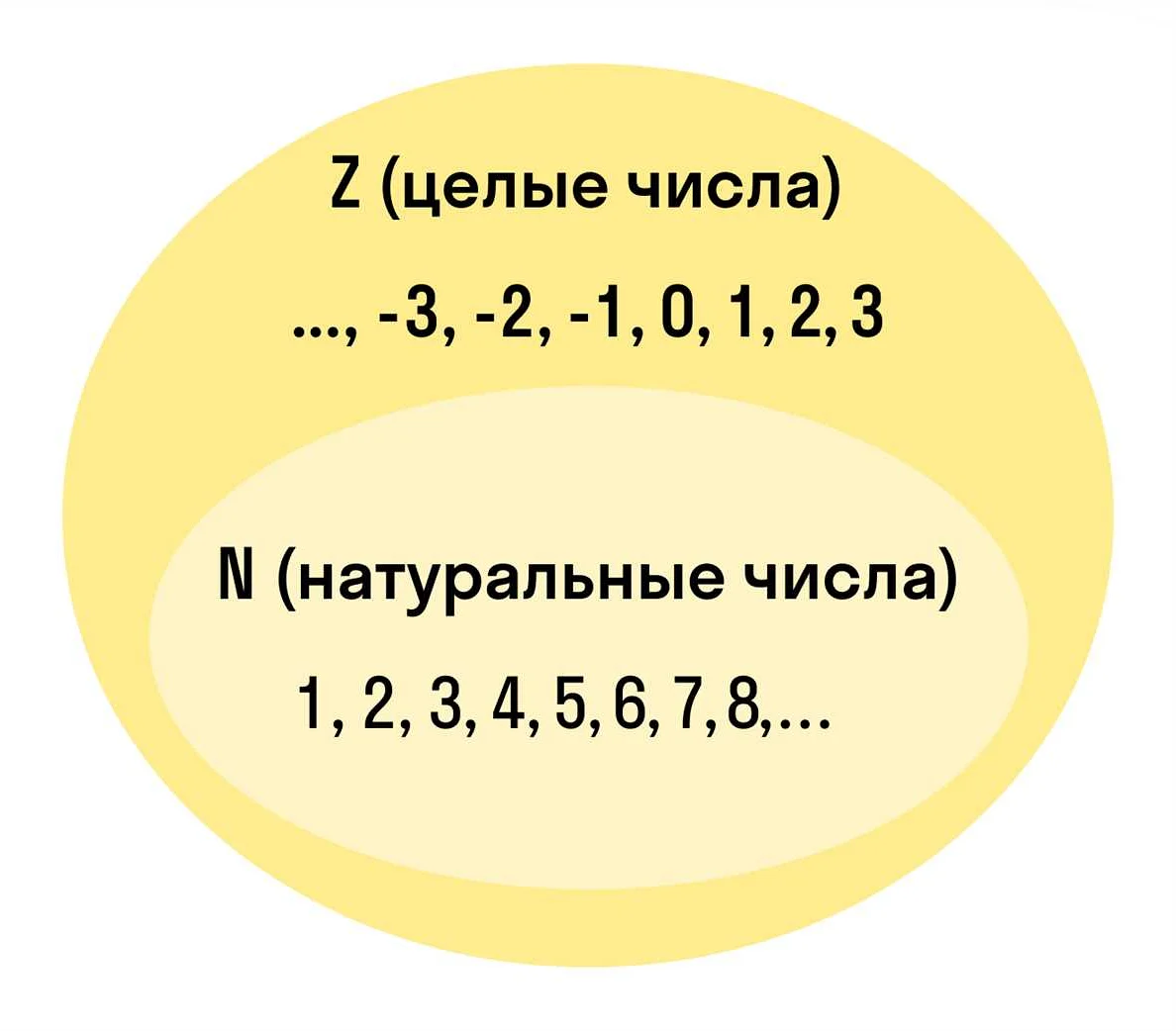
Главная особенность натуральных чисел – это то, что они не содержат нуля и отрицательных чисел. Натуральные числа отличаются от целых чисел, которые включают в себя отрицательные числа и ноль.

Натуральные числа широко используются в решении задач, счете, анализе данных и других областях математики. Они являются основой для изучения других видов чисел, таких как целые, рациональные и действительные числа.

Важно помнить, что натуральные числа – это базовый набор чисел, который мы используем в повседневной жизни и в математике для подсчета и измерения различных величин.

Видео по теме:

Понятие натуральных чисел

Натуральные числа обладают несколькими основными свойствами:

1. Натуральные числа можно складывать, вычитать, умножать и делить. Результатом этих операций также являются натуральные числа.
2. Сложение натуральных чисел подчиняется правилу коммутативности: a + b = b + a. То есть порядок слагаемых не важен.
3. Умножение натуральных чисел подчиняется правилу ассоциативности: (a * b) * c = a * (b * c). То есть порядок множителей не важен.
4. Умножение натуральных чисел также подчиняется правилу дистрибутивности: a * (b + c) = (a * b) + (a * c). То есть умножение распределено относительно сложения.

Натуральные числа позволяют нам сделать упорядоченную нумерацию предметов и удобно выполнять различные операции с количеством. Они являются базовым понятием в математике и используются в различных областях знаний.

Основные свойства натуральных чисел

Основные свойства натуральных чисел включают:

1. Закон единицы: Умножение натурального числа на единицу не меняет его значения. Например, 5 умножить на 1 равно 5.
2. Закон равенства: Если два натуральных числа равны, то их сумма или разность также будет равна. Например, если a равно b, то a + c равно b + c.
3. Закон ассоциативности: Порядок выполнения операций не влияет на результат. Например, (a + b) + c равно a + (b + c).
4. Закон коммутативности: Порядок чисел не влияет на результат операции сложения или умножения. Например, a + b равно b + a.
5. Закон распределения: Умножение натурального числа на сумму двух чисел равно сумме произведений каждого слагаемого на это число. Например, a * (b + c) равно a * b + a * c.

Эти основные свойства натуральных чисел являются основой для многих математических операций и развития алгебры.

Вопрос-ответ:

Что такое натуральные числа?

Натуральные числа — это числа, которые используются для обозначения количества элементов в конечных множествах. Они начинаются с единицы и продолжаются бесконечно. То есть, натуральные числа это 1, 2, 3, 4 и так далее.

Какие свойства имеют натуральные числа?

Натуральные числа обладают рядом основных свойств. Они образуют бесконечную последовательность, где каждое число больше предыдущего на единицу. Натуральные числа можно складывать, вычитать, умножать и делить. Кроме того, натуральные числа удовлетворяют свойству ассоциативности, коммутативности и дистрибутивности при операциях сложения и умножения.

Можно ли натуральные числа представить в виде десятичной дроби?

Нет, натуральные числа не могут быть представлены в виде десятичной дроби. Они являются целыми и не имеют десятичной части. Натуральные числа используются для подсчета количества объектов и измерения их количественных характеристик.

Какие операции можно выполнять с натуральными числами?

С натуральными числами можно выполнять операции сложения, вычитания, умножения и деления. Сложение двух натуральных чисел дает в результате третье натуральное число. Вычитание двух натуральных чисел дает в результате натуральное число или ноль. Умножение двух натуральных чисел также дает в результате натуральное число. Однако, деление натуральных чисел может давать в результате не только натуральное число, но и десятичную дробь, если деление не является точным.

Какое значение имеет ноль в натуральных числах?

Ноль не является натуральным числом. Натуральные числа начинаются с единицы и не включают ноль. Однако, ноль является целым числом и его можно использовать для обозначения отсутствия объектов или количества.

Сложение натуральных чисел

Для сложения натуральных чисел необходимо выполнить следующие шаги:

1. Выравнивание чисел по разрядам (если необходимо, дополняя одно из чисел нулями слева).
2. Сложение цифр в каждом разряде, начиная с младших разрядов.
3. Перенос разряда (если сумма цифр в разряде больше 9).
4. Запись полученной суммы.

Пример:

Сложить числа 352 и 467.

Выравниваем числа по разрядам:

352

+ 467

————

819

В результате сложения чисел 352 и 467 получаем число 819.

Сложение натуральных чисел обладает следующими свойствами:

Коммутативность: для любых натуральных чисел a и b выполняется равенство a + b = b + a.

Ассоциативность: для любых натуральных чисел a, b и c выполняется равенство (a + b) + c = a + (b + c).

Свойство нуля: для любого натурального числа a выполняется равенство a + 0 = a.

Свойство противоположности: для любого натурального числа a выполняется равенство a + (-a) = 0, где -a обозначает противоположное число к a.

Вычитание натуральных чисел

Для выполнения вычитания натуральных чисел необходимо выполнить следующие шаги:

1. Если второе число меньше первого, необходимо поменять их местами.
2. Вычитаем из каждого разряда первого числа соответствующий разряд второго числа.
3. Если разряд второго числа больше разряда первого числа, необходимо занимать единицу из более старших разрядов.
4. Полученные разности записываем друг под другом, начиная с младшего разряда.
5. Если при вычитании возникает заем, необходимо его учесть и выполнить соответствующие действия.

Пример вычитания натуральных чисел: 546 — 239 = 307.

Вычитание натуральных чисел является обратной операцией к сложению натуральных чисел.

Умножение натуральных чисел

Умножение натуральных чисел можно представить в виде повторяющегося сложения. Например, умножение числа 4 на 3 можно записать как 4 + 4 + 4 = 12.

Основные свойства умножения натуральных чисел:

1. Коммутативность: порядок сомножителей не влияет на результат умножения. Например, 3 × 4 = 4 × 3 = 12.
2. Ассоциативность: при умножении трех и более чисел порядок умножения не влияет на результат. Например, (2 × 3) × 4 = 2 × (3 × 4) = 24.
3. Распределительное свойство: умножение можно распределить на сумму или разность двух чисел. Например, 2 × (3 + 4) = 2 × 3 + 2 × 4 = 14.
4. Умножение на единицу: умножение любого числа на единицу дает то же число. Например, 5 × 1 = 5.
5. Умножение на ноль: умножение любого числа на ноль дает ноль. Например, 7 × 0 = 0.

Умножение натуральных чисел является основной операцией в арифметике и имеет широкий спектр применений в различных областях, включая финансы, науку, технику и многое другое.

Деление натуральных чисел

При делении натуральных чисел обычно выделяют две части: делимое и делитель. Делимое – это число, которое мы делим на другое число, называемое делителем. В результате деления получается частное, которое также является натуральным числом.

Например, при делении числа 10 на число 2, делимым будет число 10, а делителем – число 2. Частное будет равно 5.

Деление натуральных чисел обладает несколькими свойствами:

1. Коммутативность: порядок чисел при делении можно менять. Например, деление числа 10 на 2 даст такой же результат, как и деление числа 2 на 10.

2. Ассоциативность: результат деления не зависит от того, какие числа сначала делятся. Например, деление числа 10 на 2, а затем полученного частного на 5, даст такой же результат, как и деление числа 10 на 10, а затем полученного частного на 2.

3. Деление на единицу: любое натуральное число делится на единицу с результатом, равным самому числу.

4. Деление единицы: единица делится на любое натуральное число с результатом, равным единице.

5. Деление на ноль: деление на ноль не определено в натуральных числах.

Натуральные числа в задачах

В задачах по математике часто встречаются задания, где необходимо работать с натуральными числами. Например, задачи про сумму или разность чисел, задачи на нахождение произведения или частного, задачи на сравнение чисел по величине.

Для решения таких задач необходимо знать основные свойства натуральных чисел и уметь применять их в практике. Например, для нахождения суммы двух натуральных чисел можно использовать свойство коммутативности, которое гласит: порядок слагаемых не влияет на сумму. Также можно использовать свойство ассоциативности, которое позволяет менять порядок складывания трех и более чисел.

Для задач на нахождение произведения или частного чисел можно использовать свойства коммутативности и ассоциативности, а также свойство дистрибутивности, которое гласит: произведение двух чисел можно найти, умножив каждое число на сумму или разность других чисел.

Сравнение чисел по величине также является частой задачей в математике. Для этого используется свойство транзитивности, которое позволяет сравнивать числа поочередно, начиная с наименьшего и заканчивая наибольшим.

Знание и применение свойств натуральных чисел позволяет решать задачи более эффективно и точно. Поэтому важно разобраться в основных свойствах натуральных чисел и научиться применять их в практике.

Применение натуральных чисел в повседневной жизни

Одно из основных применений натуральных чисел — подсчет количества предметов. Например, мы считаем количество яблок в корзине или количество книг на полке. Все эти ситуации связаны с использованием натуральных чисел.

Натуральные числа также используются при измерении времени. Мы считаем количество часов, минут и секунд, чтобы определить, сколько времени прошло или сколько осталось до определенного события. Например, когда мы ждем автобус, мы смотрим на часы и считаем количество минут, оставшихся до его прибытия.

Кроме того, натуральные числа используются при измерении длины, площади и объема. Например, мы считаем количество метров в ткани, количество квадратных метров в комнате или количество литров в емкости.

Натуральные числа также используются в ситуациях, связанных с деньгами. Мы считаем количество монет или банкнот, чтобы определить сумму денег, которую мы имеем или которую нужно заплатить.

Таким образом, натуральные числа играют важную роль в нашей повседневной жизни, помогая нам считать, измерять и оценивать различные величины и количество предметов, времени или денег.