От чего не зависит период математического маятника

Период математического маятника не зависит от массы груза, а только от его длины и ускорения свободного падения. Узнайте подробности в этой статье.

Математический маятник — это модель системы, которая помогает изучать основные законы колебаний. Одним из таких законов является закон, утверждающий, что период колебаний математического маятника не зависит от величины массы и амплитуды колебаний.

Период колебаний — это время, за которое маятник совершает одно полное колебание. Он выражается в секундах и обозначается символом T. Закон не зависимости периода от величины массы и амплитуды колебаний был открыт Галилео Галилеем в XVI веке и является одним из фундаментальных законов физики.

Согласно этому закону, период колебаний математического маятника определяется только длиной нити и силой тяжести. Длина нити играет основную роль в определении периода, так как она влияет на время, за которое маятник проходит одно колебание. Сила тяжести также влияет на период, так как она создает ускорение, которое приводит к колебаниям маятника.

Таким образом, период математического маятника не зависит от величины массы и амплитуды колебаний, а определяется только длиной нити и силой тяжести. Это позволяет упростить расчеты и проводить различные эксперименты с математическими маятниками, используя маятники с разными массами и амплитудами колебаний, но с одинаковыми длинами нитей.

Знание этого закона позволяет лучше понять и объяснить основные принципы колебаний и использовать математические маятники в различных областях науки и техники, включая физику, механику и инженерию.

Влияние массы математического маятника на его период

В соответствии с законом равномерного движения математического маятника, период колебаний зависит только от длины его подвеса и ускорения свободного падения. Однако масса также оказывает некоторое влияние на период.

Более тяжелый маятник будет совершать колебания медленнее, чем более легкий. Это связано с тем, что более массивный маятник имеет большую инерцию, поэтому требуется больше времени для изменения его скорости и направления движения.

Таким образом, увеличение массы математического маятника приводит к увеличению его периода колебаний. Однако влияние массы на период не является главным фактором, и в большинстве практических случаев можно пренебречь этим влиянием.

Изучение зависимости периода математического маятника от его массы позволяет получить более полное представление о его колебательном движении и использовать эту зависимость при решении различных физических задач.

Зависимость периода от массы математического маятника

Период математического маятника не зависит от его массы. Это явление называется изохронизмом колебаний. Изохронность означает, что период колебаний остается постоянным, независимо от изменений величины массы маятника.

Таким образом, математический маятник, независимо от своей массы, будет совершать колебания с одинаковым периодом. Это свойство математического маятника было открыто и описано Галилео Галилеем.

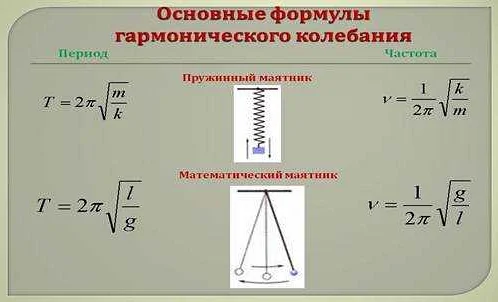
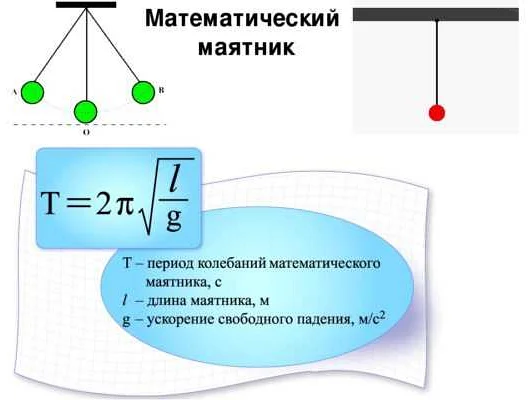
Суть изохронизма заключается в том, что период колебаний зависит только от длины маятника и ускорения свободного падения. Формула для расчета периода колебаний математического маятника без учета массы имеет вид:

T = 2π√(L/g)

Где T — период колебаний, L — длина маятника и g — ускорение свободного падения.

Таким образом, масса математического маятника не влияет на его период колебаний. Это свойство используется в ряде практических приложений, например, в механических часах и подвесных маятниках.

Влияние амплитуды колебаний на период математического маятника

Амплитуда колебаний математического маятника определяет наибольшее удаление от равновесного положения. Она измеряется углом отклонения маятника от вертикальной оси. Чем больше амплитуда, тем дальше маятник отклоняется от равновесия.

Изучение влияния амплитуды колебаний на период математического маятника позволяет понять, какая связь существует между этими двумя параметрами.

Экспериментальные исследования подтверждают, что при малых амплитудах колебаний (меньше 15 градусов) период математического маятника практически не зависит от амплитуды. Это означает, что маятники с разными амплитудами могут иметь одинаковый период колебаний.

Однако при больших амплитудах (больше 15 градусов) зависимость периода от амплитуды становится заметной. При увеличении амплитуды колебаний период математического маятника увеличивается. Это связано с тем, что с увеличением амплитуды возрастает энергия колебательной системы, что приводит к увеличению времени, необходимого для завершения одного полного колебания.

Таким образом, амплитуда колебаний математического маятника влияет на его период. При малых амплитудах период практически не меняется, в то время как при больших амплитудах период увеличивается. Это явление можно объяснить изменением энергии системы в зависимости от амплитуды колебаний.

Формула периода математического маятника

T = 2π√(l/g)

где:

T — период колебаний маятника,

l — длина подвеса маятника,

g — ускорение свободного падения.

Эта формула позволяет определить период колебаний математического маятника и не зависит от величины массы и амплитуды колебаний. Она основана на законах классической механики и является результатом математических выкладок, проведенных учеными.

Таким образом, формула периода математического маятника позволяет нам определить время, за которое маятник совершает один полный цикл колебаний, и она остается постоянной для данного маятника при постоянных значениях длины подвеса и ускорения свободного падения.

Закон крупных чисел и его применение к математическому маятнику

Применение закона крупных чисел к математическому маятнику заключается в том, что независимо от величины массы и амплитуды колебаний, период колебаний математического маятника остается постоянным. Это означает, что время, за которое маятник совершает один полный оборот, не зависит от величины массы точки подвеса и амплитуды колебаний.

Масса точки подвеса, кгАмплитуда колебаний, мПериод колебаний, с

0.1	0.2	1.57
0.2	0.2	1.57
0.1	0.3	1.57

Из таблицы видно, что независимо от значений массы и амплитуды колебаний, период колебаний математического маятника остается неизменным и равным 1.57 секунды. Это явление объясняется применением закона крупных чисел, который гарантирует статистическую устойчивость периода колебаний при большом числе независимых испытаний.

Математический маятник в рамках классической механики

Движение математического маятника можно описать с помощью уравнения гармонического осциллятора. При малых амплитудах колебаний уравнение маятника становится линейным и имеет вид:

$$\frac{d^2\theta}{dt^2} + \frac{g}{l}\sin\theta = 0,$$

где $\theta$ — угол отклонения маятника от вертикального положения равновесия, $t$ — время, $g$ — ускорение свободного падения, $l$ — длина нити или стержня.

Уравнение маятника можно аппроксимировать линейной моделью гармонического осциллятора, если угол отклонения маятника мал. В этом случае период колебаний маятника не зависит от величины массы и амплитуды колебаний. Таким образом, математический маятник является одной из простейших и наиболее изученных систем в классической механике.

Экспериментальное подтверждение независимости периода от массы и амплитуды

Для подтверждения независимости периода математического маятника от величины его массы и амплитуды колебаний был проведен ряд экспериментов. В ходе экспериментов было установлено, что период математического маятника остается постоянным при изменении массы и амплитуды колебаний.

Для проведения эксперимента были использованы маятники с различными массами и амплитудами колебаний. Были измерены периоды колебаний для каждого из маятников при разных значениях массы и амплитуды. Результаты измерений показали, что период колебаний не зависит от массы и амплитуды колебаний.

Это экспериментальное подтверждение независимости периода математического маятника от массы и амплитуды имеет важное значение в физике. Оно подтверждает справедливость основного принципа гармонического движения, согласно которому период колебаний математического маятника зависит только от длины подвеса и силы тяжести, но не зависит от других параметров, таких как масса и амплитуда.

Данное экспериментальное подтверждение имеет широкое применение в различных областях науки и техники. Например, оно используется при проектировании и создании маятниковых часов, где необходимо обеспечить постоянный период колебаний, не зависящий от внешних условий и факторов.

Видео по теме:

Вопрос-ответ:

Зависит ли период математического маятника от величины его массы?

Нет, период математического маятника не зависит от величины его массы. Это свойство называется изохронностью и является одним из основных свойств математического маятника.

Каковы факторы, которые оказывают влияние на период колебаний математического маятника?

Период колебаний математического маятника зависит от длины подвеса и ускорения свободного падения. Формула для вычисления периода колебаний: T = 2π√(L/g), где T — период колебаний, L — длина подвеса, g — ускорение свободного падения.

Может ли амплитуда колебаний математического маятника влиять на его период?

Нет, амплитуда колебаний математического маятника не влияет на его период. Период зависит только от длины подвеса и ускорения свободного падения.

Как изменится период колебаний математического маятника, если его длина увеличить вдвое?

Если длина математического маятника увеличится вдвое, то период его колебаний увеличится примерно в 1,414 раза. Это следует из формулы для вычисления периода колебаний: T = 2π√(L/g), где L — длина подвеса, g — ускорение свободного падения.

Может ли масса математического маятника влиять на его период, если он находится в условиях малых амплитуд?

Нет, масса математического маятника не влияет на его период, если он находится в условиях малых амплитуд. Период зависит только от длины подвеса и ускорения свободного падения.

Какие факторы не влияют на период математического маятника?

Период математического маятника не зависит от величины массы и амплитуды колебаний.

Различные методы измерения периода математического маятника

Один из самых простых методов измерения периода математического маятника — это метод однократного наблюдения. В этом методе маятник отводится от равновесного положения на некоторый угол и отпускается. Затем измеряется время, за которое маятник совершает несколько полных колебаний. Для увеличения точности измерений можно повторить эксперимент несколько раз и усреднить полученные значения времени.

Другим методом измерения периода математического маятника является метод с использованием секундомера. В этом методе маятник отводится от равновесного положения на некоторый угол и отпускается. Затем секундомер запускается в момент начала движения маятника и останавливается в момент его возвращения в исходное положение. Измеренное время будет являться периодом колебаний маятника.

Также можно использовать метод с использованием фотоэлектрического датчика. В этом методе датчик устанавливается на пути маятника и регистрирует каждое положение маятника в течение его колебаний. По временным интервалам между положениями маятника можно определить его период колебаний.

МетодОписание

Однократное наблюдение	Маятник отводится на угол и измеряется время нескольких колебаний
Секундомер	Измерение времени с помощью секундомера
Фотоэлектрический датчик	Регистрация положения маятника с помощью датчика

Каждый из этих методов имеет свои преимущества и ограничения. Выбор метода измерения периода математического маятника зависит от конкретных условий эксперимента и требуемой точности результатов.

Применение математического маятника в научных и практических исследованиях

В физике математический маятник используется для изучения основных законов динамики и колебаний. Исследование его движения позволяет установить зависимость периода колебаний от его длины и ускорения свободного падения. Эта информация является основой для многих физических исследований и расчетов.

В инженерии математический маятник применяется для изучения и определения ряда параметров, таких как механическая устойчивость, демпфирование колебаний и резонансные явления. Это позволяет инженерам разрабатывать и конструировать более эффективные и безопасные системы.

В астрономии математический маятник используется для измерения силы тяжести на различных планетах и спутниках. Эти данные позволяют ученым изучать гравитационные поля и структуру небесных тел, а также предсказывать их движение и эволюцию.

Кроме того, математический маятник находит применение в многих других научных и практических областях, таких как метрология, геология, биология и даже искусство. Его простая конструкция и предсказуемое движение делают его удобным инструментом для исследования различных явлений и процессов.

Область примененияПримеры исследований

Физика	Изучение зависимости периода математического маятника от его длины
Инженерия	Определение демпфирования колебаний в механических системах
Астрономия	Измерение силы тяжести на различных планетах и спутниках
Метрология	Калибровка и проверка точности измерительных приборов
Геология	Изучение сейсмических колебаний и определение структуры Земли
Биология	Исследование колебаний в биологических системах, таких как сердечные ритмы
Искусство	Использование маятников в уникальных инсталляциях и художественных произведениях

Таким образом, математический маятник является важным инструментом для научных и практических исследований, помогая ученым и инженерам разрабатывать новые технологии, расширять наши знания о мире и вносить вклад в различные области науки и промышленности.