Что показывает обратное отношение в математике

Обратное отношение в математике позволяет определить, как два числа связаны между собой. Оно показывает, какое число нужно умножить на данное, чтобы получить единицу. Понимание обратного отношения позволяет решать задачи на пропорциональность, находить обратные значения функций и многое другое. Узнайте, как использовать обратное отношение в математике для решения различных задач.

Обратное отношение – одно из важных понятий в математике, которое широко используется при решении различных задач. Оно имеет свои особенности и применяется в разных областях, таких как алгебра, геометрия и математический анализ.

Обратное отношение возникает, когда у нас есть множество элементов, и каждому элементу этого множества соответствует другой элемент из другого множества. При этом каждый элемент первого множества имеет только одно соответствие во втором множестве.

Примером обратного отношения может служить отношение «брат» в семье. Если у нас есть множество людей, то каждому человеку может соответствовать только один брат или сестра. То есть, если у нас есть человек А, то мы можем однозначно определить его брата или сестру.

Обратное отношение является важным инструментом в математике, который позволяет устанавливать связи между различными объектами и решать разнообразные задачи. Оно имеет множество применений и широко используется в разных областях науки и техники.

Решение задач, связанных с обратным отношением, часто основывается на анализе исходных данных и применении соответствующих математических методов. Для этого необходимо четко понимать определение и свойства обратного отношения, а также уметь применять их в конкретных ситуациях.

Обратное отношение в математике

Формально, обратное отношение R-1 для отношения R между множествами A и B определяется следующим образом:

Обратное отношение R-1Отношение R

(a, b) ∈ R-1

(b, a) ∈ R

То есть, если в отношении R элемент a из множества A связан с элементом b из множества B, то в обратном отношении R-1 элемент b будет связан с элементом a.

Примером обратного отношения может служить отношение «брат» между множеством людей A и множеством людей B. Если человек a является братом человека b, то в обратном отношении b будет являться братом a.

Решение задач, связанных с обратным отношением, часто включает в себя анализ отношения R и построение обратного отношения R-1. Это позволяет лучше понять связи между элементами множеств и решить поставленные задачи.

Понятие обратного отношения

Другими словами, если у нас есть отношение между множествами A и B, то обратное отношение определяет соответствие между элементами множества B и элементами множества A.

Обратное отношение отличается от исходного отношения тем, что порядок элементов в парах меняется. Например, если у нас есть отношение «больше», то его обратное отношение будет «меньше».

Пример:

Пусть у нас есть отношение «является родителем» между множеством людей A и множеством их детей B. Если Аня является родителем Миши, то обратное отношение «является ребенком» будет устанавливать соответствие между Мишей и Аней.

Примеры обратного отношения

Рассмотрим несколько примеров обратного отношения:

Исходное отношение RОбратное отношение R^-1

{(1, 2), (2, 3)}	{(2, 1), (3, 2)}
{(a, b), (b, c), (c, d)}	{(b, a), (c, b), (d, c)}
{(x, y), (y, z), (z, x)}	{(y, x), (z, y), (x, z)}

В этих примерах каждый элемент из исходного отношения R имеет пару с другим элементом в обратном отношении R^-1. Например, в первом примере элемент 1 из исходного отношения имеет пару с элементом 2 в обратном отношении.

Решение задач с обратным отношением

Обратное отношение в математике позволяет нам находить значения, входящие в обратную связь с исходными данными. Решение задач с обратным отношением требует анализа взаимосвязи между величинами и нахождения их обратных значений.

Рассмотрим пример задачи:

1. Известно, что скорость движения автомобиля составляет 60 км/ч. Найдите время, за которое автомобиль преодолевает расстояние в 120 км.

Для решения данной задачи необходимо использовать обратное отношение между скоростью и временем. Обратное отношение позволяет нам найти время, зная скорость и расстояние.

Установим пропорцию:

60 км/ч — 1 час

120 км — ? часов

Для решения пропорции можно использовать правило трех: умножить средние члены и поставить знак равенства с произведением:

60 * ? = 120 * 1

Решая пропорцию, получаем:

? = (120 * 1) / 60 = 2

Ответ: время, за которое автомобиль преодолевает расстояние в 120 км, равно 2 часам.

Таким образом, решение задач с обратным отношением требует понимания взаимосвязи между величинами и использования пропорций для нахождения обратных значений. Практика решения задач поможет закрепить этот метод и применять его на практике.

Способы выражения обратного отношения

Второй способ — использование обратных чисел. Обратное число a обозначается как 1/a. Если задано отношение a : b, то обратное отношение можно записать как 1/a : 1/b. Например, если имеется отношение 2 : 5, то обратное отношение будет выглядеть как 1/2 : 1/5.

Третий способ — использование пропорции. Если задано отношение a : b, то обратное отношение можно записать как b : a. Например, если имеется отношение 7 : 2, то обратное отношение будет выглядеть как 2 : 7.

Независимо от выбранного способа выражения обратного отношения, это понятие играет важную роль в математике и помогает решать различные задачи, связанные с пропорциями и соотношениями между числами.

Свойства обратного отношения

Свойства обратного отношения включают:

1. Симметричность: если элемент a связан с элементом b, то элемент b также связан с элементом a. То есть, если (a, b) принадлежит обратному отношению, то (b, a) также принадлежит ему.
2. Рефлексивность: каждый элемент множества связан сам с собой. То есть, для любого элемента a из множества, (a, a) принадлежит обратному отношению.
3. Транзитивность: если элемент a связан с элементом b, и элемент b связан с элементом c, то элемент a также связан с элементом c. То есть, если (a, b) и (b, c) принадлежат обратному отношению, то (a, c) также принадлежит ему.

Эти свойства позволяют нам лучше понять и анализировать обратное отношение в математике. Они помогают установить взаимосвязи между элементами множества и изучить их свойства.

Видео по теме:

Вопрос-ответ:

Что такое обратное отношение в математике?

Обратное отношение в математике — это отношение, при котором, если элемент A связан с элементом B, то элемент B также связан с элементом A. Другими словами, если a связано с b, то b связано с a.

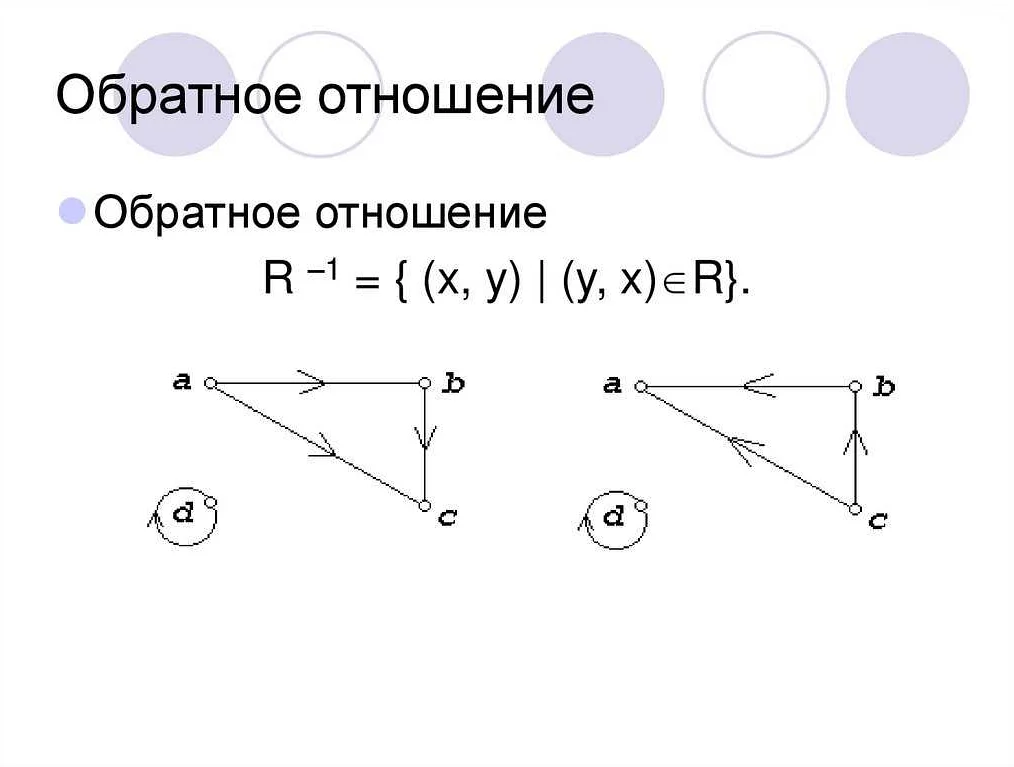
Как можно представить обратное отношение графически?

Обратное отношение можно представить графически с помощью ориентированного графа. Каждый элемент множества представляется вершиной, а связи между элементами отмечаются направленными стрелками. Если элемент A связан с элементом B, то соответствующая стрелка будет направлена от вершины A к вершине B.

Как можно найти обратное отношение для заданного отношения?

Для нахождения обратного отношения для заданного отношения нужно поменять местами все пары элементов. Если в исходном отношении есть пара (a, b), то в обратном отношении будет пара (b, a). Таким образом, обратное отношение получается путем инвертирования всех пар элементов.

Какие примеры обратного отношения можно привести?

Примеры обратного отношения можно найти в различных областях. Например, если рассматривать отношение «брат» и «сестра», то обратное отношение будет «сестра» и «брат». В математике также можно привести примеры обратных отношений, например, обратное отношение «меньше» и «больше».

Как решать задачи на обратное отношение?

Для решения задач на обратное отношение нужно анализировать связи между элементами исходного отношения и находить пары элементов для обратного отношения. Например, если задача состоит в том, чтобы найти обратное отношение для отношения «учитель» и «студент», то нужно найти пары элементов, где учитель является студентом и наоборот.

Обратное отношение и пропорциональность

Пропорциональность — это особый вид обратного отношения, при котором две величины изменяются таким образом, что их отношение остается постоянным. Если две величины x и y пропорциональны, то их отношение x/y всегда будет одним и тем же числом.

Например, если скорость движения автомобиля увеличивается, то время, затраченное на преодоление определенного расстояния, уменьшается. Здесь скорость и время являются обратно пропорциональными величинами.

Формула для обратно пропорциональных величин имеет вид:

x * y = k

где x и y — две величины, k — постоянная величина.

Решение задач, связанных с обратным отношением и пропорциональностью, часто включает использование формулы обратно пропорциональных величин, а также умение находить неизвестные значения по известным данным.

Например, если известно, что 4 кг яблок стоят 200 рублей, то можно вычислить, сколько будет стоить 6 кг яблок:

4 * 200 = 6 * x

800 = 6 * x

x = 800 / 6 = 133.33

Таким образом, 6 кг яблок будет стоить примерно 133.33 рубля.

Практическое применение обратного отношения

Например, при расчете времени, необходимого для выполнения задачи, можно использовать обратное отношение. Если работник делает определенное количество работы за определенное время, то можно найти сколько работы он сможет выполнить за другое время. Для этого нужно использовать обратное отношение, где работа будет являться обратной величиной времени.

Обратное отношение также применяется в задачах на скорость и расстояние. Например, если два объекта движутся навстречу друг другу с разными скоростями, то обратное отношение позволяет определить время встречи.

В физике обратное отношение используется при решении задач на сопротивление и проводимость. Если величина проводимости обратно пропорциональна сопротивлению, то изменение одной из этих величин влечет за собой изменение другой в обратном направлении.

Таким образом, обратное отношение играет важную роль в математике и имеет множество практических применений, помогая решать различные задачи и анализировать взаимосвязь между величинами.