Что осуществляется на третьем этапе математического моделирования
Содержимое
- 1 Что осуществляется на третьем этапе математического моделирования
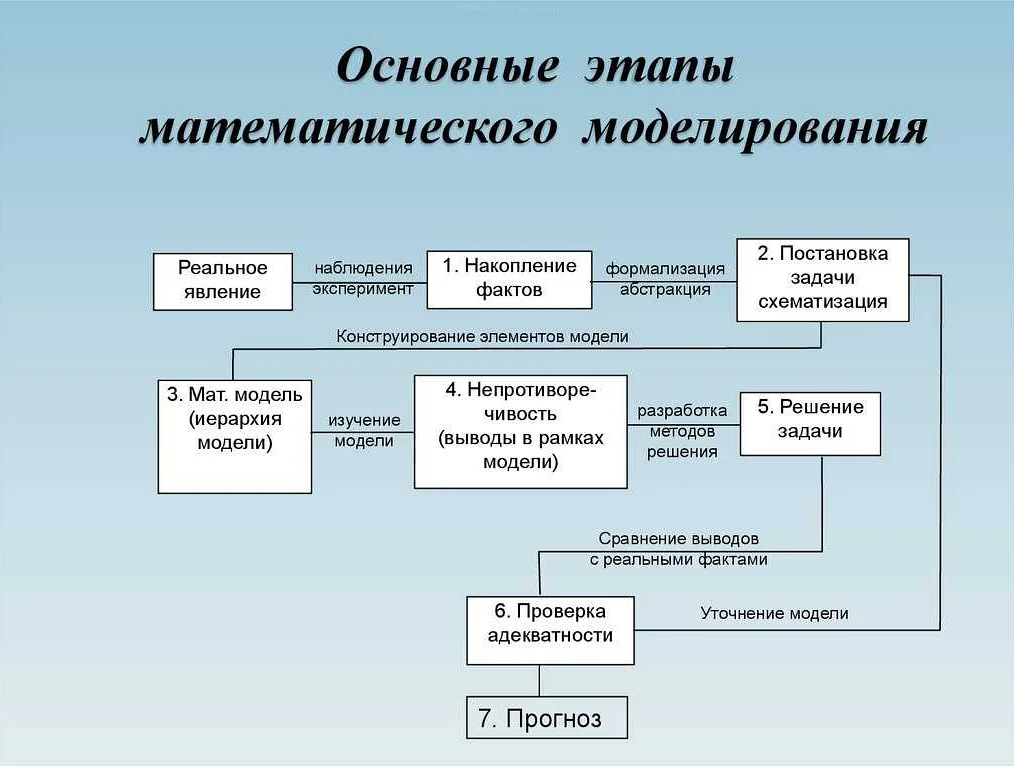
- 1.1 Основные этапы математического моделирования
- 1.2 Третий этап математического моделирования
- 1.3 Формулировка задачи
- 1.4 Выбор математической модели
- 1.5 Построение математической модели
- 1.6 Решение математической модели
- 1.7 Анализ и интерпретация результатов
- 1.8 Вопрос-ответ:
- 1.8.0.1 Какие методы используются на третьем этапе математического моделирования?
- 1.8.0.2 Какие данные необходимо учитывать на третьем этапе математического моделирования?
- 1.8.0.3 Какие преимущества имеет использование численных методов на третьем этапе математического моделирования?
- 1.8.0.4 Какие графические методы используются на третьем этапе математического моделирования?
- 1.9 Видео по теме:
На третьем этапе математического моделирования происходит анализ результатов и проверка достоверности модели. Исследователи оценивают точность предсказаний, сравнивают модельные данные с реальными наблюдениями и проводят статистические тесты. Этот этап позволяет улучшить модель и сделать ее более надежной для прогнозирования будущих событий.
Математическое моделирование играет важную роль в решении сложных задач в различных областях науки и техники. Оно позволяет создавать абстрактные математические модели, которые помогают прогнозировать и анализировать различные процессы и явления. Одним из важных этапов математического моделирования является третий этап, на котором происходит построение математической модели и ее решение.
На третьем этапе осуществляется выбор математической модели и ее построение. Для этого необходимо определить цель моделирования и выделить основные факторы, влияющие на исследуемый процесс. Затем проводится анализ полученных данных и выбирается математическая модель, которая наиболее точно и полно описывает исследуемый процесс.
После выбора модели происходит ее построение. Это включает в себя определение математических уравнений и формул, которые описывают зависимость между различными переменными. При построении модели учитываются физические законы и принятые предположения о поведении исследуемого объекта.
После построения модели следует решение уравнений и формул, которые описывают модель. Для этого применяются различные методы математического анализа, численные методы и компьютерные программы. Решение модели позволяет получить численные значения переменных и оценить поведение исследуемого процесса в различных условиях.
Основные этапы математического моделирования
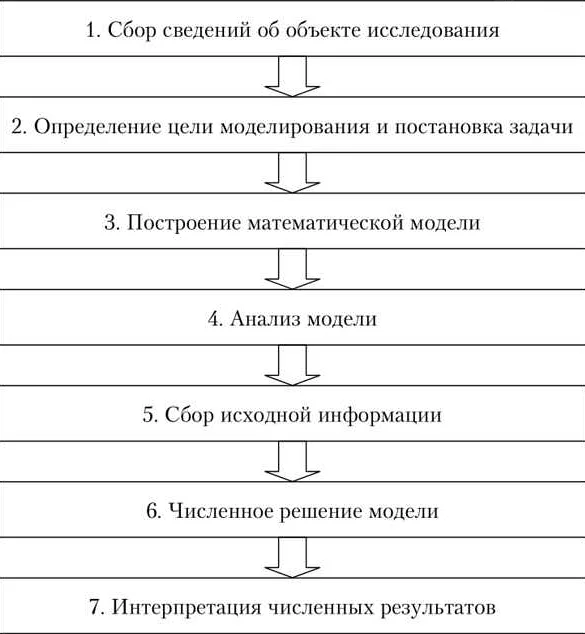
Основные этапы математического моделирования:
- Формулировка задачи моделирования. На этом этапе определяются цели и задачи моделирования, выбирается объект исследования и формулируются начальные условия.
- Построение математической модели. На этом этапе выбирается математическое описание объекта моделирования, определяются переменные, параметры и функции, которые описывают систему.
- Анализ и численное решение модели. На этом этапе производится анализ полученной математической модели, решаются уравнения и системы уравнений с помощью численных методов.
- Интерпретация и проверка результатов. На этом этапе анализируются полученные результаты моделирования, сравниваются с экспериментальными данными и делаются выводы о соответствии модели реальной системе.
- Использование модели для прогнозирования и оптимизации. На этом этапе модель используется для предсказания поведения системы в различных условиях, а также для оптимизации параметров и принятия решений.
Основные этапы математического моделирования позволяют создавать универсальные и эффективные инструменты для исследования и управления сложными системами в различных областях науки и техники.
Третий этап математического моделирования

На третьем этапе математического моделирования происходит анализ и интерпретация полученных результатов. В рамках этого этапа проводится оценка адекватности модели, а также проверка ее соответствия реальным явлениям и процессам.
Одним из основных инструментов анализа является сравнение результатов моделирования с экспериментальными данными. Если модель достаточно точно описывает наблюдаемые явления и отражает их закономерности, то она считается адекватной.
Важным этапом анализа является также идентификация параметров модели. Это процесс определения значений параметров, которые наиболее точно соответствуют реальным данным. Значения этих параметров могут быть получены путем сравнения результатов моделирования с экспериментальными данными или с помощью методов оптимизации.
После анализа и интерпретации результатов моделирования может быть проведена проверка модели на устойчивость. Это позволяет определить, как изменение параметров модели влияет на ее поведение и результаты. Если модель остается устойчивой при изменении параметров, то она считается надежной и применимой для дальнейшего использования.
Также на этом этапе модель может быть применена для прогнозирования будущих событий и явлений. Это осуществляется путем ввода новых значений параметров и анализа полученных результатов.
Третий этап математического моделирования позволяет получить важную информацию о системе, изучаемой с помощью модели. Анализ и интерпретация результатов моделирования помогают понять и объяснить наблюдаемые явления, а также прогнозировать будущие события.
Формулировка задачи

На третьем этапе математического моделирования осуществляется формулировка задачи.
Задача должна быть ясно и точно сформулирована, чтобы участники моделирования понимали ее цель и требования.
Формулировка задачи должна содержать следующие элементы:
- Описание системы – описание реальной системы, которую необходимо моделировать.
- Цель моделирования – объяснение, какую информацию или решение требуется получить с помощью моделирования.
- Параметры и переменные – определение параметров, которые будут использованы в модели, и переменных, которые будут изменяться в процессе моделирования.
- Ограничения и предположения – указание ограничений, которые накладываются на модель, и предположений, которые делаются при ее создании.
Формулировка задачи является основой для создания математической модели и позволяет определить цели и границы моделирования. Она также помогает установить связь между реальной системой и ее математическим описанием.
Выбор математической модели
Выбор математической модели зависит от множества факторов, включая цель исследования, доступные данные, а также сложность самого процесса или системы. Определение оптимальной модели требует глубокого понимания предметной области и специфики исследуемого явления.
Существует несколько подходов к выбору математической модели. Один из них — использование экспертного опыта и знаний. Эксперты, знакомые с исследуемой областью, могут предложить различные модели, которые могут быть применены для описания явления. При этом необходимо учитывать как особенности самого процесса, так и доступные данные.
Другой подход — анализ уже существующих математических моделей. В некоторых случаях может быть найдена модель, которая уже была разработана для описания подобного процесса или системы. В таком случае можно использовать данную модель, внося в нее необходимые корректировки и адаптации.
Также существуют методы построения новых математических моделей, основанные на анализе исходных данных и статистических методах. Эти методы позволяют выделить основные закономерности и зависимости в данных и на их основе построить математическую модель.
Выбор математической модели требует внимательного анализа и экспертной оценки различных аспектов исследуемого процесса или системы. От правильности выбора модели зависит точность и надежность полученных результатов, а также возможность применения модели для прогнозирования и оптимизации исследуемого явления.
Построение математической модели

Основная задача построения математической модели – установить связь между входными и выходными данными системы, определить зависимости между переменными и описать их в виде математических уравнений. Для этого необходимо анализировать и изучать объект моделирования, определять его ключевые характеристики и взаимосвязи.
При построении математической модели необходимо принимать во внимание такие факторы, как природа изучаемой системы, наличие или отсутствие статистических данных, доступность и точность экспериментальных измерений. Кроме того, важно выбрать подходящую математическую теорию и методы для описания системы.
При строительстве модели часто приходится принимать упрощения и предположения, чтобы упростить математические выкладки и сделать модель более понятной и удобной для анализа. Однако важно помнить, что каждое упрощение может вносить погрешность в результаты моделирования.
Построенная математическая модель должна быть проверена и адекватно описывать объект моделирования. Для этого проводится сравнение результатов моделирования с экспериментальными данными и реальными наблюдениями. Если модель не соответствует данным, то ее необходимо корректировать и уточнять.
Решение математической модели
Аналитическое решение предполагает поиск аналитической формулы, которая позволяет найти точное значение искомой величины в зависимости от известных параметров. Однако аналитическое решение возможно только для некоторых простых моделей, где уравнения могут быть решены аналитически с использованием известных методов.
В большинстве случаев, особенно при моделировании сложных систем, аналитическое решение невозможно или слишком сложно получить. В таких случаях применяются численные методы решения математической модели. Численное решение основывается на приближенных вычислениях, использующих дискретизацию пространства и времени и вычисление значений искомых величин на сетке точек.
Для численного решения математической модели используются различные методы, такие как метод конечных разностей, метод конечных элементов, метод конечных объемов и другие. Выбор метода зависит от особенностей модели и требований к точности и эффективности решения.
После решения математической модели получаются численные результаты, которые могут быть использованы для анализа и интерпретации системы, определения зависимостей между различными переменными, оценки поведения системы в различных условиях и принятия решений на основе полученных результатов.
Анализ и интерпретация результатов
На этом этапе математического моделирования происходит анализ полученных результатов и их интерпретация. Анализ результатов позволяет оценить качество модели и ее соответствие реальным данным.
Во время анализа результатов необходимо обратить внимание на различные аспекты моделирования, такие как точность модели, надежность результатов, статистические показатели и т. д. Анализ результатов может включать в себя сравнение модельных значений с экспериментальными данными, построение графиков и диаграмм, расчет средних значений и дисперсии.
Интерпретация результатов заключается в объяснении полученных данных и их значимости для исследуемого процесса или явления. Интерпретация результатов позволяет сделать выводы о влиянии различных факторов на исследуемый объект и предложить пути оптимизации и улучшения процесса.
Очень важно провести критический анализ результатов и учесть возможные ошибки и ограничения модели. Интерпретация результатов должна быть основана на достоверных данных и учитывать контекст и цели исследования.
Анализ и интерпретация результатов являются неотъемлемой частью математического моделирования и позволяют принять обоснованные решения на основе полученных результатов.
Вопрос-ответ:
Какие методы используются на третьем этапе математического моделирования?
На третьем этапе математического моделирования используются различные методы решения уравнений и задач, такие как численные методы, аналитические методы, графические методы и другие.
Какие данные необходимо учитывать на третьем этапе математического моделирования?
На третьем этапе математического моделирования необходимо учитывать различные данные, включая результаты экспериментов, статистические данные, предыдущие исследования и т.д. При этом важно провести анализ и обработку данных, чтобы выбрать наиболее подходящий метод решения задачи.
Какие преимущества имеет использование численных методов на третьем этапе математического моделирования?
Использование численных методов на третьем этапе математического моделирования позволяет получить приближенное решение задачи с высокой точностью. Эти методы позволяют решать сложные математические задачи, которые не могут быть решены аналитически. Кроме того, численные методы позволяют проводить моделирование в режиме реального времени.
Какие графические методы используются на третьем этапе математического моделирования?
На третьем этапе математического моделирования используются различные графические методы, такие как построение графиков, диаграмм, характеристик и т.д. Эти методы позволяют визуализировать и анализировать полученные результаты моделирования, выявить закономерности и зависимости между переменными.